Давление жидкости на криволинейные поверхности

 

Нахождение полной силы давления, построение тела давления

Величина полной силы давления на криволинейные поверхности определяется по формуле:

, (5.1)

где R_x, R_y – горизонтальные составляющие полной силы давления,

R_z – вертикальная составляющая полной силы давления.

Рассмотрение криволинейных поверхностей в модельном представлении сводят к элементарным цилиндрическим поверхностям с вертикальными или горизонтальными образующими.

Горизонтальные составляющие R_x(y) определяются из выражения:

R_x(y) = ρgH_т·ω_x(y), (5.2)

где ω_x(y) – площадь проекции цилиндрической поверхности на плоскость, перпендикулярную соответственно осям X или Y, а Н_т – расстояние от центра тяжести этой проекции до пьезометрической плоскости.

Точка приложения горизонтальных составляющих является центром давления площадей проекций ω_x(y).

Вертикальная составляющая R_z, равная весу объема жидкости, определяется из выражения:

R_z = ρgΩ_д, (5.3)

где Ω_д – представляет собой объемную эпюру давления и называется телом давления. Для вычисления величины Ω_д, необходимо выполнить построение тела давления, согласно его определения:

Телом давления называется объем призмы, ограниченный снизу цилиндрической поверхностью, а сверху – проекцией этой поверхности на пьезометрическую плоскость [1].

Вертикальная составляющая R_z проходит через центр тяжести тела давления и, в зависимости от рассматриваемой задачи, может иметь направление вниз или вверх.

Пример построения и нахождения R_x и R_z для цилиндрической поверхности с горизонтальной образующей показан на рис.5.1.

Рис.5.1. Пример построения и нахождения составляющих полной силы давления на цилиндрическую поверхность

 

Примеры решения задач

 

Пример 1. Определить величину гидростатического давления жидкости на внутреннюю поверхность стенки трубы (рис.5.2). Определить R_max - величину предельного напряжения в стенках трубы для её разрыва, если Н – напор, под которым в трубе находится жидкость; d – диаметр; L – длина трубы; δ – толщина стенки; R_х – сила давления жидкости внутри трубы, способная разорвать ее.

 

Рис.5.2

Решение. Величина R_х рассчитывается по формуле:

R_х=rgHLd, (1)

где rgH = P_max – предельная величина гидростатического давления в стенках трубы для её разрыва.

Разрывающей силе давления жидкости противодействует сила сопротивления материала стенки F:

F=2σδL, (2)

где σ – напряжение на разрыв; δ – толщина стенки; L – длина трубы; 2 – коэффициент, поскольку сила сопротивления действует с двух сторон.

При условии, что система находится в равновесии, приравняем силы давления жидкости и сопротивления материала стенки R_х=F. Подставляя из формул (1) и(2) величины, получим:

P_mLd=2δσLd или P_md=2δσ

Откуда

 

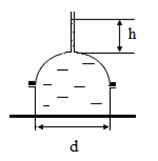
Пример 2. Вертикальный цилиндрический резервуар, диаметром d закрыт сверху полусферической крышкой того же диаметра, весом G и целиком заполнен водой (рис.5.3). Затем в отверстие в верхней части крышки ввернули вертикальную трубку пренебрежительно малого диаметра и залили в неё воду. Определить при какой высоте h вертикальная составляющая силы давления воды на крышку уравновесит ее вес.

 

Дано: d = 2м; G = 19,6 кН; r = 1000 кг/м³.

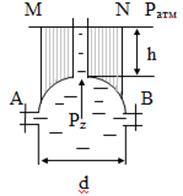
Рис.5.3

Решение. Запишем уравнение, из которого можно определить высоту h:

R_z = G.

Здесь R_z – вертикальная составляющая силы давления воды на полусферическую крышку, а G – вес крышки.

Определяем силу R_z.

Вертикальная составляющая силы давления жидкости на криволинейную поверхность равна весу жидкости в объёме давления:

R_z = r g W _{д .}

В свою очередь, чтобы построить объём давления W _д, необходимо спроецировать полусферическую поверхность крышки на пьезометрическую поверхность жидкости (то есть на ту горизонтальную плоскость, где весовое давление жидкости равно нулю). В задаче это плоскость MN. Объём, заключённый между полусферой АВ, её проекцией на плоскость MN и вертикальными проектирующими поверхностями, и есть объём тела давления (заштрихован на рисунке 5.4).

Рис.5.4

 

Из геометрических построений видно, что этот объём равен разности объёмов цилиндра и полусферы:

Определяем высоту h из уравнения: G = r g W _д, далее подставляем в результат численные значения параметров, заданных по условию и производим вычисления.

G = r g [ ] Þ

h =

 

 

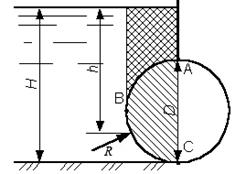
Пример 3. Определить величину, направление и точку приложения полной силы гидростатического давления воды на 1 метр ширины вальцового затвора, диаметром D, если H - уровень воды перед затвором (рис.5.5).

 

Рис.5.5

Решение. Полная сила гидростатического (избыточного) давления воды на цилиндрическую поверхность определяется по формуле 5.1:

,

где R_x – горизонтальная составляющая силы избыточного гидростатического давления, Н;

R _z – вертикальная составляющая полной силы избыточного гидростатического давления, Н. В данной задачи R_y = 0.

Горизонтальная составляющая силы избыточного гидростатического давления равна силе давления на вертикальную проекцию цилиндрической поверхности (формула 5.2):

R_x= ρgh_т·ω_x,

где h_т. – расстояние по вертикали от центра тяжести вертикальной проекции цилиндрической поверхности до уровня воды, м; ω _x – площадь вертикальной проекции цилиндрической поверхности ABC на плоскость, перпендикулярную оси Х, м².

Вертикальная составляющая силы избыточного гидростатического давления определяется по формуле 5.3:

R_z = ρgΩ_д,

где Ω_д – объем тела давления, м³

То есть вертикальная составляющая силы давления равна весу жидкости в объеме тела давления.

Тело давления представляет собой объем, расположенный над цилиндрической поверхностью и заключенный между вертикальными плоскостями, проходящими через крайние образующие цилиндрической поверхности, самой цилиндрической поверхностью и свободной поверхностью воды. Если тело давления находится со стороны, не смачиваемой жидкостью поверхности (в теле давления нет воды), то такое тело давления отрицательно и сила R_z будет направлена вверх.

В данной задаче для нахождения тела давления следует цилиндрическую поверхность ABC разделить на две: AB и BC, причем тело давления для поверхности AB будет положительным, а для BC – отрицательным. Результирующий объем тела давления на всю цилиндрическую поверхность ABC и его знак находятся путем алгебраического суммирования тел давления на криволинейные поверхности AB и BC.

Суммарная сила избыточного гидростатического давления на цилиндрическую поверхность направлена по радиусу к центру цилиндрической поверхности под углом φ к вертикали:

Расстояние h от свободной поверхности воды до точки приложения силы округлить до сантиметра.

Пример 4. Определить силу гидростатического давления на 1м ширины (b) нижней криволинейной части сосуда. Сосуд заполнен водой на глубину H = 1,5 м, r = 0,5 м (рис.5.6). Определить направление действия силы R, точку приложения силы R_x и координату вертикальной составляющей R_z.

Рис.5.6

 

Решение. Горизонтальная составляющая полной силы давления R_х равна давлению в центре тяжести проекции криволинейной поверхности на плоскость, перпендикулярную оси Х:

R_x= ρgh_т·ω_x, = ρg(H – r/2)r·b = 1000·9,81(1,5 – 0,5/2)0,5·1 = 625 кН.

Вертикальная составляющая равна весу воды в объёме тела давления:R_z = ρgΩ_д, для её нахождения необходимо построить и вычислить объём тела давления Ω_д – определяется как объем призмы ограниченной снизу кривой 1-4, а сверху её проекцией на пьезометрическую плоскость 2-3. Фигура 1-2-3-4 представляет собой тело давления на криволинейную поверхность 1-4 (рис.5.7).

Рис.5.7

R_z = ρgΩ_д = ρg (Н·r – πr²/4)b = (1000·9,81(1,5·0,5 – 3,14·0,52/4)·1 = 554 кН.

Полная сила давления на криволинейную поверхность сосуда: , в данном случае R_y = 0, подставляя значения для R_x и R_z, получим R= 835 кН. Точка приложения полный силы давления R – центр давления D, его координата L_д находится как (см.формулу 4.3):

L_д = L_т + ε = L_т + J₀/ L_тω = (Н – r/2) + br³/[12br(H –r/2)] = (1,5 – 0,5/2) + 1·0,5³/[12·1·0,5·(1,5 – 0,5/2)] = 1,267 м.

Вертикальная составляющая R_z проходит через центр тяжести фигуры 1-2-3-4, расстояние l от центра тяжести криволинейной призмы до вертикальной линии 1-2 равно статическому моменту площади фигуры I относительно этой линии, делённому на площадь фигуры, причём расстояние центра тяжести четверти круга 1-4 от вертикали 1-2 равно: х = 0,4244r:

l = I /ω_1-2-3-4 = [H·r x r/2 –(πr²/4) x 0,4244·r]/[H·r – πr²/4] = 0,263 м.

Полная сила давления R проходит через точку пересечения С линий действия горизонтальной и вертикальной составляющих под углом θ к горизонту, величина которого θ = arc tg(R_z/R_x) = arc tg(0,554/0,625) = 41⁰31'. Если криволинейная поверхность представляет собой часть круговой цилиндрической поверхности, то сила R всегда направлена по радиусу и проходит через центр круга.

 

Пример 5. Цилиндрический затвор весом G = 60 кгс, радиусом r = 0,25 м и длиной l = 100 см закрывает отверстие в дне прямоугольного резервуара размерами a x b = 30 х 100 см (рис.5.8). Определить минимальную глубину H погружения в жидкость, при которой цилиндр всплывет. Давление на свободной поверхности p₀ = 0,9 кгс/см², γ = 1 г/см³.

Рис.5.8

Решение. Пример решения приведён в размерности СГС.

В данном случае горизонтальная составляющая равна нулю (слева и справа силы, действующие на цилиндрическую поверхность по горизонтали противоположно направленные, т.е. компенсированы). Вертикальная составляющая R_z равна весу жидкости в объёме тела давления: R_z =ρgΩ_д = ρg[a·b(H – c) – b(ω₁ + 2ω₂)].

 

Рис.5.9

 

Из рисунка 5.9 определим определим угол α: sin(α/2) = a/2r =0,3/(2x0,25) = 0,6 откуда α = 73⁰44'. Угол β = 180⁰ –α = 106⁰16'. Площади сегметов ω₁ и ω₂ определяем по формулам:

ω₁ = (r²/2)(πα/180⁰ –sinα) = 0,0102 м², ω₂ = (r²/2)(πβ/180⁰ –sinβ) = 0,0279 м². С = 2rsin(β/2) = 0,4 м.

Давление над свободной поверностью жидкости отлично от атмосферного (р_атм = 1 кгс/см²), поэтому, выталкивающая сила, действующая на цилиндрический затвор будет равна:

F = (р_атм – р₀)a·b = (1 – 0,8)х30х100 = 600 кгс. Из уравнения равновесия для цилиндра, с учетом его веса: G + R_z = F, выразим R_z = F – G. Отсюда, учитывая зависимость R_z = f(H), запишем R_z =ρgΩ_д = ρg[a·b(H – c) – b(ω₁ + 2ω₂)] = 1·[0,3(H – 0,4) – 1·(0,0102 + 2x0,0279)] = 600 –60. Из полученного соотношения находим H = 242 см.

Ответ: H = 242 см.