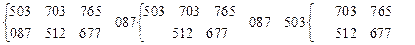Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод Шелла (сортировка с убывающем шагом).Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
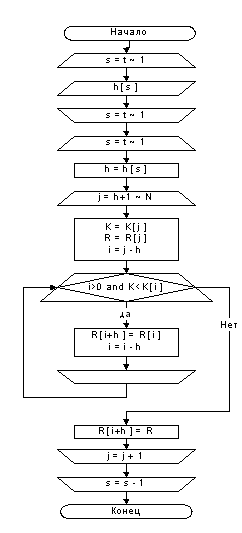
Записи R1,…, RN перемещаются на том же месте. После завершения сортировки их ключи будут упорядочены: К1 £ … £К N. Для управления процессом сортировки используются вспомогательная последовательность шагов h t h t-1,…, h 1, где h 1=1. Правильно выбрав эти приращения, можно значительно сократить время сортировки. При t = 1 алгоритм сводится к алгоритму простой вставки.
(Цикл по j). Установить h:= ht, и выполнить шаги Ш3 – Ш6 при h < j £ N. (для сортировки элементов, отстоящих друг от друга на h позиций, воспользуемся простыми вставками и в результате получим К t £ К t + h при 1£ i £ N – h. (Установить i, К, R). Установить i = j – h, К=К j , R = R j . (Сравнить К, К i ) Если К>=К i , то перейти к шагу Ш6. (Переместить Ri , уменьшить i). Установить R i + h = R i , затем i =i– h. Если i > 0, то возвратиться к шагу Ш4. (R на место Ri+ h ) Установить Ri+ h = R.
На выбор шагов ht, ht-1,…, h1 значительно влияет условие делимости: hs+1 mod hs = 0, при t > s >= 1.
Применяя метод Шелла со всего двумя шагами, можно существенно сократить время по сравнению с простыми вставками с 0(N2) до 0(N1.667). Если использовать больше шагов, то можно добиться лучших результатов.
Быстрая сортировка "Быстрая сортировка" Хоару. В методе пузырька последовательность сравнений предопределена: каждый раз сравниваются одни и те же пары ключей независимо от того, что мы могли узнать о файле из предыдущих сравнений. Обратимся теперь к совсем иной стратегии, при которой используется результат каждого сравнения, чтобы определить, какие ключи сравнивать следующими. В этом алгоритме для сортировки элементов массива А[1],..., А[п] из этих элементов выбирается некоторое значение ключа v в качестве опорного элемента, относительно которого переупорядочиваются элементы массива. Желательно выбрать опорный элемент близким к значению медианы распределения значений ключей так, чтобы опорный элемент разбивал множество значений ключей на две примерно равные части. Далее элементы массива переставляются так, чтобы для некоторого индекса j все переставленные элементы А[1],..., A[j] имели значения ключей, меньшие чем v, а все элементы A[j + 1],..., А[п] — значения ключей, большие или равные v. Затем процедура быстрой сортировки рекурсивно применяется к множествам элементов А[1],..., A[j] и A[j + 1],..., А[п] для упорядочивания этих множеств по отдельности. Поскольку все значения ключей в первом множестве меньше, чем значения ключей во втором множестве, то исходный массив будет отсортирован правильно. Теперь начнем разрабатывать рекурсивную процедуру quicksort(i, j), которая будет работать с элементами массива А, определенным вне этой процедуры. Процедура quicksort(i, j) должна упорядочить элементы A[i],..., А[j]. Предварительный набросок процедуры показан в листинге 8.5. Отметим, что если все элементы A[i],..., A[j] имеют одинаковые ключи, над ними не производятся никакие действия. Напишем функцию findpivot (нахождение опорного элемента) проверяющую, все ли элементы А[i],..., А[j] одинаковы. Если функция findpivot не находит различных ключей, то возвращает значение 0. В противном случае она возвращает индекс наибольшего из первых двух различных ключей. Этот наибольший ключ становится опорным элементом. Код функции findpivot приведен в листинге 8.6.
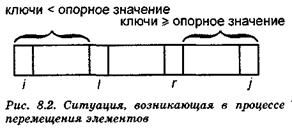
Листинг 8.6. функция findpivot function findpivot (i, j: integer): integer; Var firstkey: keytype; { примет значение первого найденного ключа, т.е. A[i].key } k: integer; { текущий индекс при поиске различных ключей) Begin firstkey:= A[i].key; for k:=i+l to j do { просмотр ключей } if A[k].key > firstkey then { выбор наибольшего ключа} begin result:=k’exit; end else if A[k].key < firstkey then begin result:=i; exit; end result:=0; {различные ключи не найдены } end; { findpivot } Теперь реализуем строку, где необходимо переставить элементы A[i],..., A[j] так, чтобы все элементы с ключами, меньшими опорного значения, располагались слева от остальных элементов. Чтобы выполнить эти перестановки, введем два курсора l и r, указывающие соответственно на левый и правый концы той части массива А, где в настоящий момент мы переставляем (упорядочиваем) элементы. При этом считаем, что уже все элементы А[i],..., А [ l- 1], расположенные слева от l, имеют значения ключей, меньшие опорного значения. Соответственно элементы А[r+ 1],..., А[j], расположенные справа от r, имеют значения ключей, большие или равные опорному значению (рис. 8.2). Нам необходимо рассортировать элементы А[l],..., А[r].
Сначала положим l = i и r = j. Затем будем повторять следующие действия, которые перемещают курсор l вправо, а курсор r влево до тех пор, пока курсоры не пересекутся. 1. Курсор перемещается l вправо, пока не встретится запись с ключом, не меньшим опорного значения. Курсор r перемещается влево, также до тех пор, пока не встретится запись с ключом, меньшим опорного значения. Отметим, что выбор опорного значения функцией findpivot гарантирует, что есть по крайней мере одна запись с ключом, значение которого меньше опорного значения, и есть хотя бы одна запись со значением ключа, не меньшим выбранного опорного значения. Поэтому обязательно существует "промежуток" между элементами A[i] и А[j], по которому могут перемещаться курсоры l и. r. 2. Выполняется проверка: если l > r (на практике возможна только ситуация, когда l = r + 1), то перемещение элементов A[i],..., A[j] заканчивается. 3. В случае l < r (очевидно, что случай l = r невозможен) переставляем местами элементы А[1] и A[r]. После этого запись А[1] будет иметь значение ключа меньшее, чем опорное значение, a A[r] — большее или равное опорному значению. Курсор l перемещается на одну позицию от предыдущего положения вправо, а курсор r — на одну позицию влево. Далее процесс продолжается с пункта l. Описанный циклический процесс несколько неуклюжий, поскольку проверка, приводящая к окончанию процесса, расположена посредине. Если этот процесс оформить в виде цикла repeat, то этап 3 надо переместить в начало. Но в этом случае при l = 1и r = j сразу меняются местами элементы A[i] и A[j], независимо от того, надо это делать или нет. Но с другой стороны, это несущественно, так как мы не предполагаем первоначальное упорядочивание элементов A[i],..., А[j]. Функция partition (разделение), которая выполняет перестановки элементов и возвращает индекс l, указывающий на точку разделения данного фрагмента массива А на основе заданного опорного значения pivot, приведена в листинге 8.7. Листинг 8. Функция partition function partition (i, j: integer; pivot: keytype): integer; Var l, r: integer; { курсоры } Begin (1) L:= i; (2) r:= j; Repeat (3) swap(A[l], A(r]); (4) while A[l]..key < pivot do (5) I:= 1+1; (6) - while A[r].key >= pivot do (7) r:= r - 1 Until (8) 1 > r; result:= l; end; { partition } Код программы quicksort (быстрая сортировка) программы приведен в листинге 8.8. Для сортировки элементов массива А типа аггау [1.. n ] of recordtype надо просто вызвать процедуру quicksort(l, n). Листинг 8.8. Процедура быстрой сортировки И; s procedure quicksort (i, j: integer); { сортирует элементы A[i],..., A[j] внешнего массива А } Var pivot: keytype; { опорное значение } pivotindex: integer; { индекс элемента массива А, чей ключ равен pivot } k: integer; {начальный индекс группы элементов, чьи ключи >= pivot} Begin (1) pivotindex:= findpivot(i, j); (2) if pivotindex <> 0 then Begin { если все ключи равны, то ничего делать не надо } (3) pivot:= A[pivotindex] .key; (4) k:= portitiond, j, pivot); (5) quicksort (i, k-l); (6) quicksort(k, j) End end; { quicksort }
Пирамидальная сортировка
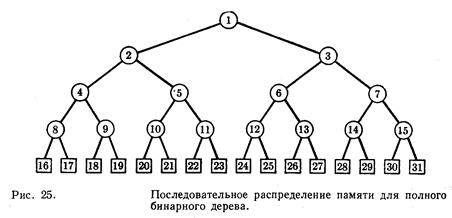
На приведено полное бинарное дерево с 16 концевыми узлами, такие деревья удобно хранить в последовательных ячейках памяти (массиве) на показано на Рис. 2.
Рис. 2 Последовательное распределние памяти для полного бинарного дерева Заметим, что отцом узла с номером k является [k/2], а его потомками является узлы с номерами 2k и 2k+1. Это еще одно преимущество использование нисходящего метода – удобна нумерация ячеек. До сих пор предполагалось что N есть степень 2, в действительности можно работать с произвольным количеством концевых элементов. Пирамидальная сортировка. Будем называть файл ключей К1, К2, …, КN "пирамидой", если К[j/2] ³ Кj при 1 £ [j/2] < j £ N. (1) В этом случае К1 ³ К2, К1 ³ К3, К2 ³ К4. и т.д. именно это условие выполняется на рис. Из этого следует, что К1 = mах(К1, К2, …, КN). (2) Начальная задача состоит в том, чтобы произвольный последовательный файл преобразовать в пирамиду. Эффективный подход предложил Р.У.Флойд. Пусть нам удалось расположить файл таким образом, чтобы К[j/2] ³ Кj при l < [j/2] < j £ N, (3) где l - некоторое число ³ 1. (В исходном файле (не упорядоченном) это условие "автоматически" выполняется только для l = [N / 2], поскольку ни один индекс j не удовлетворяет условию [N/2] £ [j/2] < j £ N.) Далее изменяя лишь поддерево с корнем в узле l, преобразовать файл, чтобы распространить неравенство (3) и на случай [j/2]= l. Следовательно, можно уменьшать l на 1, до тех пор, пока не будет достигнуто условие (1). Эти идеи Уильямса и Флойда приводят к изящному алгоритму. Алгоритм У (пирамидальная сортировка). Записи R1, R2, …, RN переразмещаются на том же самом месте; после завершения сортировки их ключи будут упорядочены: К1£ …£ КN. Сначала файл перестраивается в пирамиду, после чего вершина пирамиды многократно исключается и записывается на свое окончательное место. Предполагается, что N ³ 2. (Начальная установка) l:=[N/2]+1, r:=N. (Уменьшить l или r) Если l > 1, то установить l:=l -1, R:=R l , К:=К j. (Если l >1, это означает, что происходит процесс преобразования исходного файла в пирамиду; если же l= 1, то это значит, что ключи К1, К2, …,Кr уже образуют пирамиду.) В противном случае установить R:=Rr, К:=Кr, Rr:=R1 и r:=r-1; если в результате оказалось, что r=1, то установить R1:=R и завершить работу алгоритма. (Приготовиться к "протаскиванию") Установить j:= l. (К этому моменту К[j/2] ³ Кj при l < [j/2] < j £ r (4), а записи Rk, r < k £ N, занимают свои окончательные места. Шаги У3–У8 называют алгоритмом "протаскивания"; их действие эквивалентно установке R l = R с последующим перемещением записей R l,…,Rr таким образом, чтобы условие (4) выполнилось и при [j/2] = l.) (Продвинуться вниз) Установить i:=j и j:=2j (в последующих шагах i=[j/2].) Если j<r, то перейти к шагу У5; если j=r, то перейти к шагу У6; если же j>r, то перейти к шагу У8. (Найти "большего" сына) Если Кj < Кj+1, то установить j:=j+1. (Больше К?) Если К³Кj, то перейти к шагу У8. (Поднять его вверх). Установить Ri:=Rj и возвратиться к шагу У4. – алгоритм (Занести R) Установить Ri:= R (На этом алгоритм "протаскивания", начатый на шаге У3, заканчивается). Возвратиться к шагу Н2.
Рис. 3 Процесс пирамидальной сортировки.
Листинг 8.10. Процедура pushdown procedure pushdown (first, last: integer); { Элементы A[first],..., A[last] составляют частично упорядоченное дерево за исключением, возможно, элемента A[first] и его сыновей. Процедура pushdown восстанавливает частично упорядоченное дерево } Var r: integer; { указывает текущую позицию А[first] } Begin r: = first; { инициализация } while r <= last div 2 do if last = 2*r then Begin { элемент в позиции r имеет одного сына в позиции 2*r } if A[r].key > A[2*r].key then swap(A(r], A[2*г]); r:= last { досрочный выход из цикла while } End else { элемент в позиции r имеет двух сыновей в позициях 2*r и 2*r+1} if A[r] .key > A [2*r] .key and A[2*r] .key <= A[2*r + 1] .key then begin { перестановка элемента в позиции r с левым сыном } swap(A[r], A [2*r]); r:= 2*r End else if A[r] .key > A [2*r + 1] .key and A[2*r + 1] .key < A[2*r].key then begin { перестановка элемента в позиции г с правым сыном } swap(A[r], A[2*r + 1]); r:= 2*r + 1 End Else {элемент в позиции r не нарушает порядок в частично упорядоченном дереве } r:= last { выход из цикла while } end; { pushdown } Вернемся к листингу 8.9 и займемся строками (4) - (6). Выбор минимального элемента в строке (4) прост — это всегда элемент А[1]. Чтобы исключить оператор печати в строке (5), мы поменяли местами элементы А[1] и A[i] в текущей куче. Удалить минимальный элемент из текущей кучи также легко: надо просто уменьшить на единицу курсор i, указывающий на конец текущей кучи. Затем надо вызвать процедуру pushdown(l, i - 1) для восстановления порядка в частично упорядоченном дереве кучи А[1],..., A[i - 1]. Вместо проверки в строке (3), не является ли множество S пустым, можно проверить значение курсора i, указывающего на конец текущей кучи. Теперь осталось рассмотреть способ выполнения операторов в строках (1), (2). Можно с самого начала поместить элементы списка L в массив А в произвольном порядке. Для создания первоначального частично упорядоченного дерева надо последовательно вызывать процедуру pushdown(j, п) для всех j = n/2, n/2 - 1,..., 1. Легко видеть, что после вызова процедуры pushdown(j, n) порядок в ранее упорядоченной части строящегося дерева не нарушается, так как новый элемент, добавляемый в дерево, не вносит нового нарушения порядка, поскольку он только меняется местами со своим "меньшим" сыном. Полный код процедуры heapsort (пирамидальная сортировка) показан в листинге 8.11. Листинг 8.11. Процедура пирамидальной сортировки % procedure heapsort; { Сортирует элементы массива А[1],..., А[n] в убывающем порядке } Var i: integer; { курсор в массиве А } Begin { создание частично упорядоченного дерева } (1) for i:= n div 2 downto 1 do (2) pushdown (i, n); (3) for i:= n downto 2 do Begin (4) swap(A[l], A[i]); { удаление минимального элемента из кучи } (5) pushdown (1, i - 1) { восстановление частично упорядоченного дерева } End end; { heapsort } Сортировка подсчетом Правомерен вопрос: всегда ли при сортировке n элементов нижняя граница времени выполнения имеет порядок W(n logn)? Ранее были рассмотрены алгоритмы сортировки и их нижние границы времени выполнения, когда о типе данных ключей не предполагается ничего, кроме того, что их можно упорядочить посредством некой функции, показывающей, когда один ключ "меньше чем" другой. Часто можно получить время сортировки меньшее, чем О(n log n), но необходима дополнительная информация о сортируемых ключах. Метод сортировки подсчетом основан на том, что j й ключ в окончательно упорядоченной последовательности превышает ровно (j – 1) из остальных ключей. Иначе говоря, если известно, что некоторый ключ превышает ровно 27 других, то после сортировки соответствующая запись должна занять 28 е место. Т.о. идея состоит в том, чтобы сравнить попарно все ключи и подсчитать, сколько из них меньше каждого отдельного ключа. Очевидный способ выполнить сравнения – ((сравнить Кj с К i)при 1 £ j £ N) при 1£ i £ N, но легко видеть, что более половины этих действий излишни, поскольку не нужно сравнивать ключ сам с собой, и после сравнения Ка с Кс не надо сравнивать Кс с Ка. Поэтому достаточно ((сравнить К j с К i ) при 1£ j £ i) при 1£ i £ N. Итак, приходим к следующему алгоритму.
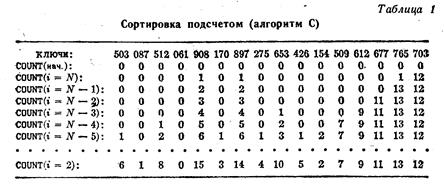
Алгоритм "сравнение и подсчет" Алгоритм С (сравнение и подсчет). Этот алгоритм сортирует записи R1, …, RN по ключам К1, …, К N , используя для подсчета число ключей, меньших данного, вспомогательную таблицу Кол[1],…,Кол[ N ]. После завершения алгоритма величина Кол [ j ]+1 определяет окончательное положение записи R j . (сбросить счетчики) Установить Кол[1],…,Кол[ N ] равными нулю. (Цикл по i) Выполнить шаг 3 при i = N, N–1, …, 2, затем завершить работу; (Цикл по j). Выполнить шаг 4 при j = i –1, …, 1. (Сравнить Кi с Кj .) Если Кi < Кj , то увеличить Кол[ j ] на 1, в противном случае увеличить Кол[ i ] на 1. Работа алгоритма изображена на Рис. 4 Заметим, что в этом алгоритме записи не перемещаются. Он аналогичен сортировке таблицы адресов, поскольку массив Кол определяет конечное расположение записей; но эти методы несколько различаются, потому что Кол[ j ] указывает на то место, куда надо переслать запись Rj , а не ту запись, которую надо переслать на место Rj . Кроме того, в алгоритме не сказано ни слова о случае, если ключи равные. Однако шаг 4 неявно оговаривает и этот случай.
Рис. 4 Сортировка подсчетом. Достоинством этого алгоритма является его простота. Однако он не достаточно эффективен. Алгоритм "разделение и обмен". Существует другая разновидность сортировки посредством подсчета, которая важна с точки зрения эффективности; она применима, если имеется много равных ключей и все они подпадают под диапазон а £ К j £ с, где значение (с–а) не велико. Эти предположения на первый взгляд весьма ограничивают сферу использования этого алгоритма, однако он найдет применение при сортировки старших цифр ключа, после чего последовательность окажется частично отсортирована. Предположим, что все ключи лежат между 1 и 100. При первом просмотре файла можно подсчитать, сколько имеется ключей, равных 1, 2, …, 100, а при втором просмотре можно уже располагать записи в соответствующих местах области вывода.
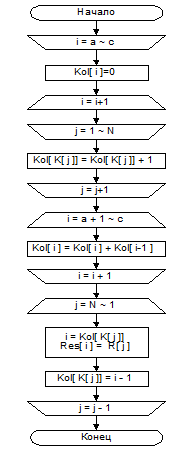
Алгоритм Д (распределяющий подсчет). Этот алгоритм предполагает, что все ключи – целые числа в диапазоне а £ Кj £ с при 1£ i £ N, сортирует записи R1,…,RN, используя вспомогательную таблицу Кол[а]…Кол[с]. Результат располагается в массиве Рез. (Сбросить счетчики) Установить Кол[a]…Кол[с] равным нулю. (Цикл по j) Выполнить шаг Д3 при 1£ j £ N, затем перейти к Д4. (Увеличить т.е. подсчитать количество ключей со значением К j) Увеличить значение Кол[К j ] на 1. (Цикл по i) Выполнить шаг Д5 при а+1 £ i £ с, затем перейти к Д6. (Суммирование для вычисление числа ключей меньших или равных i) Установить Кол[ i ]:= Кол[ i ] + Кол[ i – 1 ] (Цикл по j – перебираем все N записей, начиная с последней) Выполнить шаг Д7 и Д8 при j=N, N –1,…,1 затем перейти к Д9. (Позиционирование R j в массиве Рез) Установить i:= Кол[К j ], Рез i :=Rj (Идем с конца массива Кол таким образом, чтобы очередная (j я) запись по порядку следования в исходном массиве среди всех записей с одинаковыми ключами в результирующем массиве займет последнее место (т.е. i) из тех мест, которые могли бы занять записи с ключем Кj). (Уменьшить Кол[Кj], для того, чтобы это значение указывало на свободный номер в массиве Рез, который находится перед тем номером, куда положили Rj на шаге Д7 ) Кол[К j]:=i – 1. Конец Впервые эта быстрая сортировка была разработана в 1954 году Х.Сьювордом и использовался при поразрядной сортировке).
Сортировка слиянием. Слияние означает объединение двух или более упорядоченных файлов в один упорядоченный файл. Можно, например, слить два подфайла 503 703 765 и 087 512 677, получив 087 503 512 677 703 765. Простой способ сделать это –сравнить два наименьших элемента, вывести наименьший из них и повторить эту процедуру, т.е.
Необходимо предусмотреть тот случай, когда один файл исчерпан.
|
|||||
|
Последнее изменение этой страницы: 2017-01-18; просмотров: 661; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.181.194 (0.009 с.) |

 (Цикл по р) Выполнить шаг Ш2 при р = t, t –1, …, 1, после чего завершить алгоритм.
(Цикл по р) Выполнить шаг Ш2 при р = t, t –1, …, 1, после чего завершить алгоритм.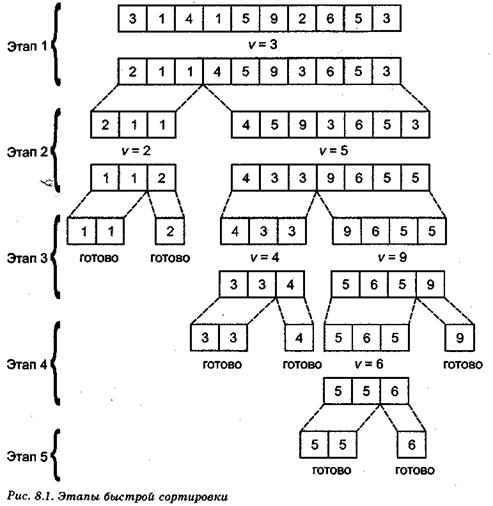
 Пирамидальную сортировку иногда описывают как это обозначение указывает на характер изменения переменных l и r. Верхний треугольник соответствует фазе построения пирамиды, когда r=N, а l убывает до 1. На Рис. 3 показан процесс пирамидальной сортироки для тех же 16 чисел.
Пирамидальную сортировку иногда описывают как это обозначение указывает на характер изменения переменных l и r. Верхний треугольник соответствует фазе построения пирамиды, когда r=N, а l убывает до 1. На Рис. 3 показан процесс пирамидальной сортироки для тех же 16 чисел.