Сортировка простым (фиксированным) двухпутевым слиянием.

В алгоритме Е границы между отрезками полностью определяются "ступеньками вниз". Такой подход обладает тем возможным преимуществом, что исходные файлы с преобладанием возрастающего или убывающего расположения элементов могут обрабатываться очень быстро, но при этом замедляется основной цикл вычислений. Вместо проверок ступенек вниз можно принудительно установить длину отрезков, считая, что все отрезки исходного файла имеют длину 1, после первого просмотра все отрезки (кроме, быть может, последнего) имеют длину 2, …, после k^го просмотра имеют длину 2^k. В отличие от "естественного" слияния в алгоритме Е такой способ называется простым (или фиксированным) двухпутевым слиянием.

 

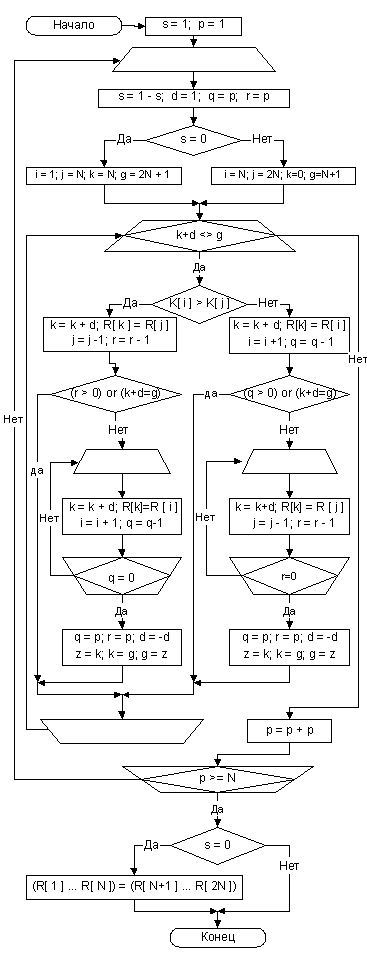
Пример работы алгоритма Ф приведен на Рис. 6. Этот метод справедлив и тогда, когда N не является степенью 2, сливаемые отрезки не все имеют длину 2^k. Проверки ступенек заменены уменьшением длины переменных q и r и проверкой на равенство нулю. Благодаря этому время асимптотически приближается к 11Nlоg₂N, что несколько лучше, чем в предыдущем алгоритме.

На практике имеет смысл комбинировать алгоритм Ф с простыми вставками; вместо первых четырех просмотров алгоритма Ф можно простыми вставками отсортировать группы, скажем из 16 элементов, исключив тем самым довольно расточительные вспомогательные операции, связанные со слиянием коротких файлов.

 

Рис. 6 Сортировак простым двухпутевым слиянием

 

Алгоритм Ф (Сортировка простым двухпутевым слиянием).

При сортировке записей R₁, …, R_N используются две области памяти, каждая из которых может содержать N записей. Для удобства обозначим записи, находящиеся во второй области, через R_N+1, …, R_2N, хотя в действительности области не обязательно идти друг за другом. Начальное содержание второй области не имеет значение. После завершения алгоритма ключи будут упорядочены К₁ £ …£ К_N.

(Начальная установка) Установить s:=0, (при s=0 мы будем пересылать записи из области (R₁,…R_N) в область (R_N+1, …, R_2N); при s=1 наоборот.) p:=1 (p – размер возрастающих отрезков, которые будут сливаться во время текущего просмотра; q и r – количества неслитых элементов в отрезках) (переменные i, j, k, g указывают текущие позиции во входных "файлах", откуда идет чтение, и в "выходных" файлах, куда идет запись)

(Подготовиться к просмотру) Если s=0, то установить i:=1, j:=N, k:=N+1, g:=2N, если s=1, то установить i:=N+1, j:=2N, k:=1, g:=N. Затем установить d:=1, q:=p, r:=p.

(Сравнения К_i с К_j) Если К_i > К_j, то перейти к шагу Ф8.

(Пересылка R_i) Установить k:=k+d, R_k:=R_i.

(Конец отрезка?) Установить i:=i+1, q:=q–1. Если q > 0, то возвратиться к шагу Ф3.

(Пересылка R_j) Установить k:=k+d. Если k=g, то перейти к шагу Ф13; в противном случае установитьR_k:=R_j.

(Конец отрезка?) Установить j:=j–1, r:=r–1. Если r > 0, то возвратиться к шагу Ф6; в противном случае перейти к шагу Ф12.

(Пересылка R_j) Установить k:=k+d, R_k:=R_j.

(Конец отрезка?) Установить j:=j–1, r:=r–1. Если r > 0, то возвратиться к шагу Ф3.

(Пересылка R_i) Установить k:=k+d, Если k=g, то перейти к шагу Ф13; в противном случае установить R_k:=R_i.

(Конец отрезка?) Установить i:=i+1, q:=q–1. Если q > 0, то возвратиться к шагу Ф10

(Переключение направления) Установить q:=p, r:=p, d:= –d и взаимозаменить k:=g. Возвратиться к шагу Ф3.

(Переключение областей) Установить p:=p+p. Если p < N, то установить s:=1 – s и возвратиться к шагу Ф2. В противном случае сортировка завершена; Если s=0, то установить (R₁,…R_N):= (R_N+1, …, R_2N). (Независимо от распределения исходного файла последнее копирование будет выполнено тогда и только тогда, когда значение round(log₂N) нечетно. Так что можно заранее предсказать положение отсортированного файла, и копирование, как правило, не требуется).