
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свободные колебания упругих тел.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим сначала задачу на собственные колебания. Решение уравнений движения будем искать в виде
Здесь В дальнейшем для удобства через
Внешние силы и граничные условия в случае свободных колебаний должны быть нулевыми, при этом множитель Уравнения связи между амплитудами напряжений и деформаций сохраняют форму обычных уравнений закона Гука
Система уравнений (7) при однородных граничных условиях может иметь очевидное тривиальное решение
Однако при некоторых значениях параметра
Соответствующие значения параметра Уравнения, связывающие величины
Очевидно, что вследствие однородности системы уравнений и граничных условий искомые функции, входящие в (8), определены с точностью до произвольного множителя. Уравнения (1) могут рассматриваться как уравнения статической задачи теории упругости с массовыми силами
или
Так как
Это равенство выражает свойство ортогональности собственных формколебаний. Из условия ортогональности следует, в частности, что частоты
Из условия ортогональности следует
Но это равенство возможно лишь тогда, когда Поскольку
Соотношения (9) выражают условия нормирования и одновременно повторяют условия ортогональности собственных форм. Перейдем теперь к исследованию свободных колебаний. Принцип суперпозиции (метод Фурье) позволяет представить общее выражение для перемещений при свободных колебаниях упругого тела следующим образом:
Здесь
Приравнивая при
Умножаем каждое из этих равенств на
Следует заметить, что соотношения (11) не предполагают возможности разложения функций
|
|||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 420; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.159.123 (0.006 с.) |

 .
. — функция только координат, но не времени. Аналогичным образом представляются компоненты деформации и напряжения.
— функция только координат, но не времени. Аналогичным образом представляются компоненты деформации и напряжения. ,
,  будем обозначать амплитуды перемещений и напряжений, т.е. вместо
будем обозначать амплитуды перемещений и напряжений, т.е. вместо  будем в дальнейшем писать
будем в дальнейшем писать  . (7)
. (7) сокращается.
сокращается. .
. .
. возможно и ненулевое решение
возможно и ненулевое решение .
. — собственные частоты упругого тела, а функции
— собственные частоты упругого тела, а функции  определяют собственные формы колебаний. Заметим, что в (7) войдут квадраты собственных частот, которые сохранятся при всех дальнейших выкладках, поэтому корню
определяют собственные формы колебаний. Заметим, что в (7) войдут квадраты собственных частот, которые сохранятся при всех дальнейших выкладках, поэтому корню  . Мы не будем вводить для этих отрицательных корней специальную нумерацию, но следует помнить, что кроме решения
. Мы не будем вводить для этих отрицательных корней специальную нумерацию, но следует помнить, что кроме решения  всегда присутствует и второе решение
всегда присутствует и второе решение  . Это замечание позволяет образовывать из них действительные комбинации, которые одни только и имеют механический смысл.
. Это замечание позволяет образовывать из них действительные комбинации, которые одни только и имеют механический смысл. , вытекают из (7):
, вытекают из (7): . (8)
. (8) . Пусть
. Пусть  представляет собой перемещение, вызванное действием распределенных по объему сил
представляет собой перемещение, вызванное действием распределенных по объему сил  . Аналогичным образом силы
. Аналогичным образом силы  при частоте
при частоте  вызывают перемещение
вызывают перемещение  . Но по теореме Бетти
. Но по теореме Бетти ,
,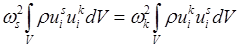 .
. , то последнее равенство возможно, если интеграл равен нулю. Следовательно,
, то последнее равенство возможно, если интеграл равен нулю. Следовательно, .
. . Уравнение для нахождения собственных частот будет обязательно иметь еще один комплексно сопряженный корень
. Уравнение для нахождения собственных частот будет обязательно иметь еще один комплексно сопряженный корень  . Соответствующие собственные формы также будут комплексно сопряженными:
. Соответствующие собственные формы также будут комплексно сопряженными: .
. .
. ,
,  . Таким образом, в линейной теории упругости движений с комплексными частотами быть не может. Очевидно, что этим исключается и случай чисто мнимых частот.
. Таким образом, в линейной теории упругости движений с комплексными частотами быть не может. Очевидно, что этим исключается и случай чисто мнимых частот. . (9)
. (9) . (10)
. (10) ,
,  — неопределенные константы. Дифференцируя (10) по времени, находим
— неопределенные константы. Дифференцируя (10) по времени, находим .
. значения перемещений и скоростей их заданным начальным значениям
значения перемещений и скоростей их заданным начальным значениям 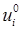 и
и  , получим
, получим .
. и интегрируем по объему. Вследствие (9) в левой части от каждого ряда остается лишь по одному члену
и интегрируем по объему. Вследствие (9) в левой части от каждого ряда остается лишь по одному члену . (11)
. (11)


