
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Постановка динамической задачи теории упругостиСодержание книги
Поиск на нашем сайте
Динамические задачи теории упругости (часть 1)
Многие внешние воздействия на сооружения носят ярко выраженный динамический характер. Хотя при этом перемещения оказываются обычно небольшими, однако скорости и, главное, ускорения могут достигать величин, опасных для конструкции. К таким нагрузкам относятся сейсмические толчки, ветровые порывы, а также различные динамические воздействия технологического происхождения: движение поездов, кранов, неуравновешенных частей машин и механизмов. Как известно из курса теоретической механики, ускоренные или замедленные движения масс вызывают инерционные силы, воздействующие на элементы конструкции так же, как и статические нагрузки. Особенностью динамических нагрузок является то, что в большинстве случаев они вызывают колебания, причем при периодическом повторении малых динамических воздействий в определенных условиях происходит накопление энергии системы. Постепенно увеличивается размах колебаний, а вместе с ним и интенсивности инерционных сил до очень больших значений. Это явление особенно опасно для сооружения, т.к. разрушение может произойти при малых воздействиях и в конструкциях, достаточно прочных по отношению к обычным статическим нагрузкам. Здесь исследуются колебания упругих и неупругих элементов конструкций с бесконечным числом степеней свободы.
Динамические задачи теории упругости (часть 1)
Динамические задачи теории упругости (часть 1)
Многие внешние воздействия на сооружения носят ярко выраженный динамический характер. Хотя при этом перемещения оказываются обычно небольшими, однако скорости и, главное, ускорения могут достигать величин, опасных для конструкции. К таким нагрузкам относятся сейсмические толчки, ветровые порывы, а также различные динамические воздействия технологического происхождения: движение поездов, кранов, неуравновешенных частей машин и механизмов. Как известно из курса теоретической механики, ускоренные или замедленные движения масс вызывают инерционные силы, воздействующие на элементы конструкции так же, как и статические нагрузки. Особенностью динамических нагрузок является то, что в большинстве случаев они вызывают колебания, причем при периодическом повторении малых динамических воздействий в определенных условиях происходит накопление энергии системы. Постепенно увеличивается размах колебаний, а вместе с ним и интенсивности инерционных сил до очень больших значений. Это явление особенно опасно для сооружения, т.к. разрушение может произойти при малых воздействиях и в конструкциях, достаточно прочных по отношению к обычным статическим нагрузкам. Здесь исследуются колебания упругих и неупругих элементов конструкций с бесконечным числом степеней свободы.
Постановка динамической задачи теории упругости Применяя принцип Д'Аламбера, можно получить уравнения движения упругого тела из уравнений равновесия, добавив к действующим массовым силам
Таким образом, уравнения движения будут следующие:
Остальные уравнения (равновесия, совместности деформаций, Коши) и граничные условия сохраняются, но теперь к ним нужно добавить начальные условия
Аналогично (1) из уравнений Ламе получаем уравнения движения в перемещениях однородной изотропной упругой среды
Часто бывает удобно представить поле перемещений в виде
Здесь
Если поле массовых сил также представить в подобном виде
то уравнения движения в перемещениях удовлетворяются, если потенциалы перемещений являются решениями следующих уравнений:
где величины
имеют размерность скорости и соответственно носят название скоростей распространения волн растяжения-сжатия и формоизменения. Таким образом, для однородной изотропной упругой среды замкнутая система уравнений движения в потенциалах перемещений состоит из (4) и (3). Начальные условия (2) для нее должны быть записаны в потенциалах
где
Отметим, что, несмотря на независимость уравнений (4), как правило, в начально-краевых задачах они связаны граничными условиями. Сформулированную динамическую задачу теории упругости называют нестационарной. Ее признак — наличие в постановке задачи инерционных членов в уравнениях движения и начальных условий. Частный случай этой задачи — свободные колебания. В этом случае упругое тело свободно от действия внешних сил, Рассмотрение предельных случаев нестационарной задачи приводит к стационарнымдинамическим задачам. Их признак — отсутствие начальных условий. К ним относятся задачи о собственных и вынужденных гармонических колебаниях, а также задачи о прогрессивных волнах. Собственные колебания. Под ними понимается задача на собственные значения (собственные частоты) для однородных уравнений теории упругости при однородных граничных условиях (отсутствуют внешние силы, перемещения на поверхности Вынужденные гармонические колебания. В этом случае объемные силы
Величины с верхним индексом «*» не зависят от времени, поэтому в качестве типового представителя функции
Действительно, любая периодическая функция может быть представлена рядом Фурье. Построив решение для одного члена этого ряда, мы можем воспользоваться принципом суперпозиции для построения полного решения. Прогрессивные волны. Под ними понимается частные решения уравнений динамической теории упругости, соответствующие волнам, распространяющимся вдоль прямой при отсутствии начальных условий.
|
||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 840; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.192.248 (0.008 с.) |

 силы инерции:
силы инерции: .
. . (1)
. (1)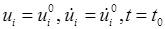 . (2)
. (2)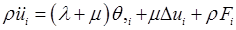 .
. . (2а)
. (2а) и
и  — скалярный и векторный потенциалы перемещений. Для однозначности потенциалов перемещений необходимо дополнительное условие, которое, как правило, принимают
— скалярный и векторный потенциалы перемещений. Для однозначности потенциалов перемещений необходимо дополнительное условие, которое, как правило, принимают . (3)
. (3) ,
, , (4а)
, (4а) , (4б)
, (4б) ,
, ,
,
 ,
,  на
на  . Часть поверхности
. Часть поверхности  может быть неподвижно закреплена, на ней
может быть неподвижно закреплена, на ней  . Заданы начальные условия (2), которые приводят тело в движение сообщением ему начального распределения перемещений и скоростей.
. Заданы начальные условия (2), которые приводят тело в движение сообщением ему начального распределения перемещений и скоростей. , поверхностные силы
, поверхностные силы  и заданные перемещения точек поверхности
и заданные перемещения точек поверхности 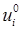 представляют собой периодические функции времени, такие, что
представляют собой периодические функции времени, такие, что .
.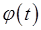 можно принять
можно принять



