
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Неравенство Рэлея и метод Ритца.Содержание книги Поиск на нашем сайте
Умножим обе части уравнения (7)
на
Преобразуя числитель интегрированием по частям при однородных граничных условиях (интеграл по поверхности будет равен нулю), получим
и
Если Покажем, что функционал, фигурирующий в правой части формул (16), (17), позволяет получить оценку, по крайней мере, для наименьшей из собственных частот. Условимся нумеровать собственные частоты в порядке возрастания, так что
Выберем в качестве
А так как вследствие (8)
то, умножив на
Совершенно аналогично вследствие ортогональности главных форм
Теперь соотношение (16) можно переписать следующим образом:
или
Но каждый член ряда в числителе не меньше соответствующего члена ряда в знаменателе, так как
Здесь Неравенство (18) дает верхнюю оценку для низшей частоты колебаний упругого тела. Если функции
Отсюда
или, полагая
Наиболее простой результат получается, когда параметры
Уравнения (19) линейны и однородны; для существования нетривиального решения необходимо, чтобы детерминант системы был равен нулю. Это условие приводит к алгебраическому уравнению
|
||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 567; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.212.119 (0.006 с.) |

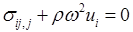
 , проинтегрируем по объему и решим полученное равенство относительно
, проинтегрируем по объему и решим полученное равенство относительно  . Тогда
. Тогда . (16)
. (16)
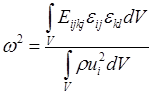 . (17)
. (17) , то уравнение (7) выполняется при
, то уравнение (7) выполняется при  и формула (16) либо (17) даст точное значение квадрата собственной частоты с номером
и формула (16) либо (17) даст точное значение квадрата собственной частоты с номером  . Но если
. Но если  .
. .
. ,
, и проинтегрировав, получим
и проинтегрировав, получим .
.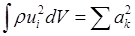 .
.
 .
. , поэтому
, поэтому  и (17) можно заменить неравенством Рэлея
и (17) можно заменить неравенством Рэлея . (18)
. (18) — упругий потенциал, вычисленный для заданной системы перемещений
— упругий потенциал, вычисленный для заданной системы перемещений  — выражение кинетической энергии, в которой скорости заменены перемещениями
— выражение кинетической энергии, в которой скорости заменены перемещениями  , то
, то  и
и  . Наилучшим приближением для
. Наилучшим приближением для  будут значения
будут значения  .
. ,
, ,
, . (19)
. (19) . (20)
. (20) будет стремиться к величине
будет стремиться к величине  , при этом нельзя сказать — сверху или снизу. Доказательство этой теоремы здесь не приводится. Следует заметить, что для ее выполнения необходима полнота системы функций
, при этом нельзя сказать — сверху или снизу. Доказательство этой теоремы здесь не приводится. Следует заметить, что для ее выполнения необходима полнота системы функций  , т.е. возможность представления любой допустимой системы перемещений
, т.е. возможность представления любой допустимой системы перемещений 


