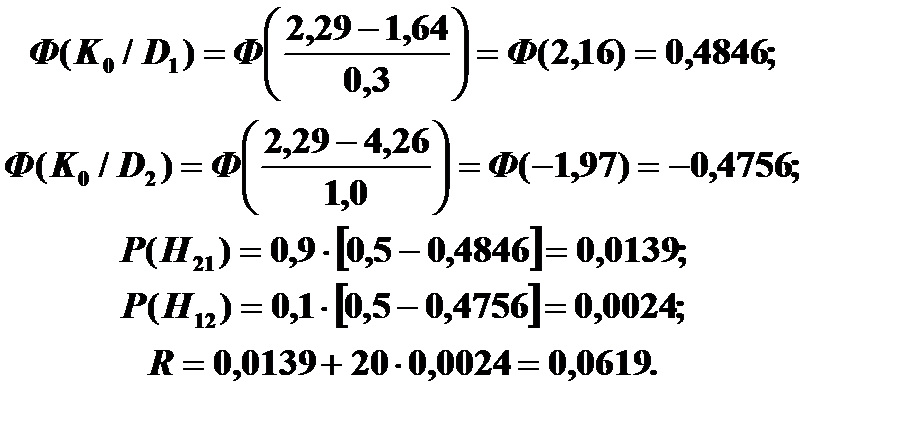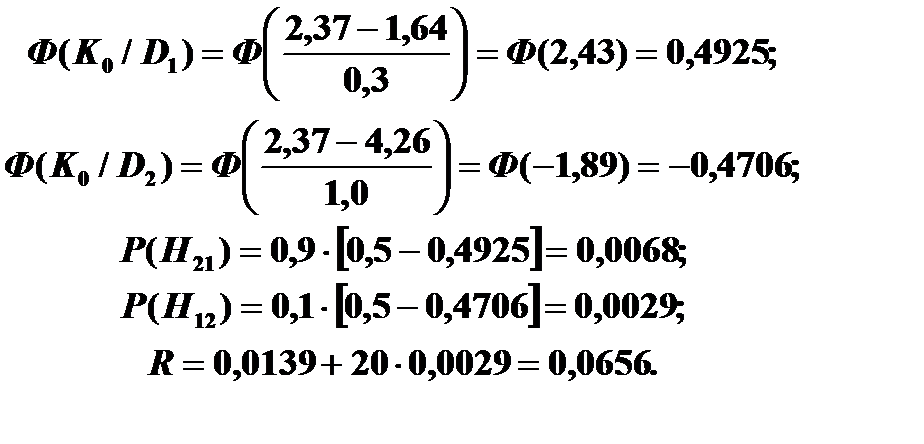Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод минимального числа ошибочных решенийСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
В этом методе стоимости решений принимаются одинаково, и отношение правдоподобия принимает вид
Решение аналогично методу минимального риска. Метод наибольшего правдоподобия Здесь отношение априорных вероятностей исправного (Р 1) и неисправного (Р 2) состояний принимается равным единице, а условие нахождения K0 выглядит так:
Пример Определить предельное значение параметра K 0, выше которого объект подлежит снятию с эксплуатации. Объект - газотурбинный двигатель. Параметр - содержание железа в масле K, (г/т). Параметр имеет нормальное распределение при исправном (D 1) и неисправном (D 2) состояниях. Известно:
Решение Метод минимального риска Согласно выражению (2.4) После подстановки выражения
и логарифмирования получаем
Преобразуя и решая данное квадратное уравнение, получим: K01 =2,24; К02 =0,47. Искомое граничное значение К0 =2,24. Метод минимального числа ошибочных решений Условие получения K 0: Подставляя и раскрывая соответствующие плотности вероятностей, получаем уравнение:
Подходящим корнем этого уравнения является величина 2,57. Итак, K 0 = 2,57. Метод наибольшего правдоподобия Условие получения К0: F(K0/D1) = F(K0/D2). Итоговое квадратное уравнение будет выглядеть так:
Искомое K0 = 2,31. Определим вероятность ложной тревоги P(H 21 ), вероятность пропуска дефекта Р(Н12), а также величину среднего риска R для граничных значений K0, найденных различными методами. Если в исходных условиях K1<K2, то
Если в исходных условиях K1> K2, то
Для метода минимального риска при K0 =2,29 получаем следующее
Для метода минимального числа ошибочных решений при K0 =2,57:
Для метода наибольшего правдоподобия при K 0 =2,37:
Сведем результаты расчетов в итоговую таблицу.
Задания к задаче №2. Вариант задания выбирается по двум последним цифрам номера зачетной книжки. Во всех заданиях требуется определить граничное значение K 0, разделяющее объекты на два класса: исправный и неисправный. Результаты решений наносятся на график (рис. 9.1), который строится на миллиметровке и вклеивается в работу.
Итак, техническое диагностирование объекта осуществляется по параметру K. Для исправного объекта даются среднее значение параметра K 1 и среднеквадратическое отклонение σ 1. Для неисправного соответственно K2 и σ 2. В исходных данных также для каждого варианта приводится соотношение цен C12/C21. Распределение K принимается нормальным. Во всех вариантах P1 =0,9; P2 =0,1. Варианты заданий приведены в табл. 2.1-2.10.
Исходные данные к вариантам 00÷09 (табл. 2.1): Объект - газотурбинный двигатель. Параметр - виброскорость (мм/с). Неисправное состояние - нарушение нормальных условий работы опор ротора двигателя.
Таблица 2.1
Исходные данные к вариантам 10÷19 (табл. 2.2): Объект - газотурбинный двигатель. Параметр - концентрация примесей меди (Cu) в масле (г/т). Неисправное состояние - повышенная концентрация Cu в масле из-за интенсификации процессов изнашивания омедненных шлицевых соединений приводных валов. Таблица 2.2
Исходные данные к вариантам 20÷29 (табл. 2.3): Объект - подкачиваемый топливный насос топливной системы. Параметр - давление топлива на выходе (кг/см2). Неисправное состояние - деформация крыльчатки.
Таблица 2.3
Исходные данные к вариантам 30÷39 (табл. 2.4):
Объект - газотурбинный двигатель. Параметр - уровень виброперегрузок (g). Неисправное состояние - раскатка наружной обоймы подшипников.
Таблица 2.4
Исходные данные к вариантам 40÷49 (табл. 2.5): Объект - межвальный подшипник газотурбинного двигателя. Параметр - показания виброакустического прибора контроля состояния подшипника (µа). Неисправное состояние - появление следов выкрашивания на беговых дорожках подшипника. Таблица 2.5
Исходные данные к вариантам 50÷59 (табл. 2.6) Объект - газотурбинный двигатель. Параметр - содержание железа (Fe) в масле (г/т). Неисправное состояние - повышенная концентрация Fe в масле из-за ускоренного изнашивания зубчатых соединений в коробке приводов. Таблица 2.6
Исходные данные к вариантам 60÷69 (табл. 2.7): Объект - масло для смазки газотурбинного двигателя. Параметр - оптическая плотность масла, %. Неисправное состояние - пониженные эксплуатационные свойства масла, имеющего оптическую плотность. Таблица 2.7
Исходные данные к вариантам 70÷79 (табл. 2.8): Объект - топливные фильтроэлементы. Параметр - концентрация примесей меди (Cu) в масле (г/т). Неисправное состояние - повышенная концентрация Cu в масле из-за интенсификации процессов изнашивания омедненных шлицевых соединений приводных валов. Таблица 2.8
Исходные данные к вариантам 80÷89 (табл. 2.9) Объект - аксиально-поршневой насос. Параметр - величина производительности насоса, выражаемая объемным КПД (в долях от 1,0). Неисправное состояние - низкое значение объемного КПД, связанное с поломкой насоса. Таблица 2.9
Исходные данные к вариантам 90÷99 (табл. 2.10) Объект - система управления самолета, состоящая из жестких тяг. Параметр - суммарный осевой люфт сочленений, мкм. Неисправное состояние - повышенный суммарный осевой люфт из-за износа сопрягаемых пар. Таблица 2.10
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 983; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.42.199 (0.012 с.) |

 (2.5)
(2.5) (2.6)
(2.6)
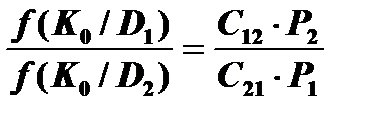
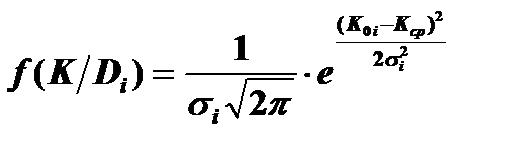
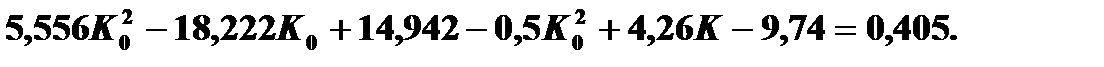

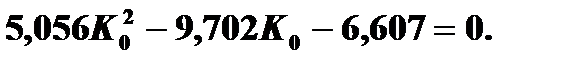
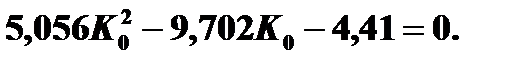
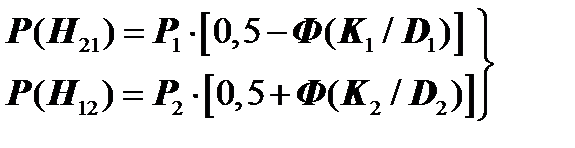 и
и 
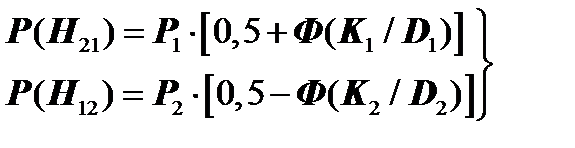 и
и