
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача №3. Решение задач прогнозирования состояния объекта ⇐ ПредыдущаяСтр 5 из 5
Большая группа задач в диагностике авиационных конструкций относится к оценке их перспективных ресурсов (сроков службы) на основании данных о динамике изменения технического состояния. Как известно, решение таких задач связано с использованием моделей изменения технического состояния объекта по наработке, которая представляет собой корреляционную функцию связи между случайными значениями диагностических параметров и наработкой объекта. Случайной (корреляционной) функцией называется функция, значения которой имеют случайное распределение для каждого значения аргумента. Применительно к нашей задаче случайная функция является аппроксимирующей линией, описывающей совокупность диагностических параметров K на интервале наработки Δt. Термин "случайная функция" в такой трактовке является синонимом понятия "математическая модель". Решение прогностических задач может быть реализовано с позиций двух подходов: изучения моделей изменения физических механизмов случайных процессов; изучения моделей изменения признаков, сопровождающих случайные процессы (принцип "черного ящика"). Итак, в каждый момент времени случайная функция представляет собой случайную величину, имеющую непрерывное, как правило, нормальное распределение. В каждом сечении наработки можно построить такое распределение, зная его медиану Моделью процесса изменения состояния объекта по наработке будет линия, аппроксимирующая все точки Наиболее универсальным способом аппроксимаций случайных выборок является метод наименьших квадратов. Рассмотрим метод наименьших квадратов в простейшем виде. Пусть имеется N экспериментальных точек с координатами Kj, ti и требуется подобрать полином п -го порядка
который наилучшим образом описывает экспериментальные данные. По методу наименьших квадратов коэффициент ai выбирают так, чтобы квадратичная погрешность между каждой из точек аппроксимирующей линии была минимальной
Так как погрешность зависит от выбранных значений коэффициентов a0, а1,..., ап, то из условия
относительно неизвестных а0, а1,..., ап.
Рассмотрим простейший случай линейной аппроксимации. В общем виде уравнение прямой линии ‒ у = а0 + а1 • п. Система уравнений для нахождения коэффициентов а0, а1 будет выглядеть так:
Решая эту систему, находим
где Kk,t - второй смешанный центральный момент,
Пример Рассмотрим построение модели изменения состояния опор двигателя по диагностическому признаку "время выбега ротора". На первом этапе необходимо оценить наличие корреляционной связи между временем выбега ротора и наработкой подшипников (рис. 9.2). Для этого по замеренным значениям времени выбега τ построим график.
Испытанию на выбег подвергались подшипники с эксплуатационной наработкой 0, 700, 1067, 2100, 2122, 3826, 4174, 4348, 6000, 6153, 6382, 6400, 6938, 10114 часов. Общая тенденция расположения точек позволяет предположить, что имеет место линейная корреляционная связь между t и τ. В этом случае выяснение степени тесноты связи полученной совокупности производится по коэффициенту корреляции ρ. Как известно,
где Кτ,t - второй смешанный центральный момент; σt - среднеквадратическое отклонение по наработке; στ - среднеквадратическое отклонение по выбегу. Входящие в формулу (3.5) величины подсчитываются по следующим зависимостям:
где τi,
n - число вертикальных сечений по наработке. По результатам расчета После подстановки получаем ρ = ‒ 0,52. Знак минус указывает на наличие отрицательного тренда, а абсолютное значение 0,52 свидетельствует о достаточно тесной корреляционной связи между τ и t. Далее строим корреляционную функцию (медианы), аппроксимирующую изменение τ по t.
Рис. 9.2. К вопросу оценки корреляционной связи между наработкой t и временем выбега ротора τ
Для этого находим сначала центры тяжести (медианы) распределений каждой из частичных выборок в сечениях, соответствующих вышеотмеченным наработкам (рис. 9.3).
Рис. 9.3. Построение корреляционной функции (модели) методом
наименьших квадратов Затем полученную совокупность точек описываем прямой линией (так как вначале мы предположили линейную корреляцию) по методу наименьших квадратов. Согласно этому методу в уравнении прямой линии общего вида τ=a·t + b;
где mτ, mt - математические ожидания соответственно времени выбега и наработки. После соответствующих подстановок получаем уравнение модели τ = 56,7 ‒ 0,0015· t Технология построения доверительных интервалов следующая. 1. Сначала находим ширину разброса для трех произвольно взятых распределений (рис. 9.3) согласно соотношению ± δ = v ·στ, где v - табличный коэффициент, зависящий от принятого уровня вероятности и количества экспериментальных точек (для Р =0,997 v =3,0). 2. Через три точки, соответствующие нижним границам каждого из распределений, проводим среднюю линию верхнего и нижнего доверительного интервала модели. В таком виде модель пригодна для решения задач прогнозирования ресурса двигателя по параметру "выбег ротора". Наименьшая величина выбега (по ТУ) составляет 40 с. Используя нижний доверительный интервал функции τ=f(t), находим предельную наработку tпр =5200 ч. Задания к задаче №3. Вариант задания выбирается по последней цифре шифра студента согласно табл. 3.1. Количественная величина и физическая природа параметров K1 и K2, а также предельное значение параметра K0, берутся из предыдущего задания для метода статистических решений.
Таблица 3.1
Далее строится картина расположения исходных значений диагностических параметров на графике по следующей технологии: интервал изменения диагностического параметра из предыдущей задачи откладывается по оси ординат графика (рис. 9.4); откладываются равномерные отрезки наработки на оси абсцисс в соответствии с заданием табл. 3.1; на каждом из сечений наработки произвольно откладывается ряд точек случайных значений диагностических параметров, имея в виду, что: на 1-м сечении располагается 5 точек (наработка 0); на 2-м сечении располагается 6 точек; на 3-м сечении располагается 7 точек; на 4-и сечении располагается 8 точек; на 5-м сечении располагается 9 точек; на 6-м сечении располагается 10 точек; на 7-м сечении располагается 5 точек; на 8-м сечении располагается 6 точек; на 9-м сечении располагаются 7 точек.
Необходимо учитывать, что часть вариантов имеет отрицательный тренд (например, когда речь идет о КПД и т.п.). К примеру, для 1 варианта исходное распределение случайных диагностических параметров на графике будет выглядеть следующим образом (рис. 9.5). Имеем: диагностический параметр – виброскорость; среднее значение виброскорости при нулевой наработке =35 мм/с; интервал наработки Δt =0÷5000 ч; количество сечений n =6.
Среднее значение виброскорости на 6-м сечении =65 мм/с. Строим исходный график с учетом количества точек на каждом сечении (рис. 9.5). Необходимо построить аппроксимирующую функцию (модель) изменения виброскорости по наработке. Расчеты и графические построения производят в соответствии с технологией примера, приведенного в разделе 9.5.
Рис. 9.5. Пример нанесения исходной выборки и определения предельной наработки
Определение предельной наработки осуществляется следующим образом: Предельное значение K0 откладывается на оси ординат; из этой точки проводится горизонтальная линия, параллельная оси абсцисс; предельную наработку определяет точка пересечения горизонтальной линии с верхним или нижним доверительным интервалом построенной модели, в зависимости от физической сущности описанного процесса. В данном случае предельная наработка будет определяться точкой пересечения с верхним доверительным интервалом. График чертится на миллиметровой бумаге и вклеивается в работу.
Приложение 1 Значения функции Лапласа Ф(z)
СОДЕРЖАНИЕ Введение ………………………………………………………………………..3 1. Учебный план дисциплины «Техническая диагностика» ………. ……....4 2. Основные сведения о дисциплине …………………………………………4 3. Рекомендуемая литература ……………………………………………..…..6 4. Электронный адрес кафедры для консультаций ……………………….…6 5. Структура дисциплины ………………………………………………….….7 6. Учебная программа дисциплины и методические указания к изучению тем программы …………………………………………………..….7 7. Терминология (понятийный аппарат) дисциплины …………………..…..10 8. Лабораторные занятия ………………………………………………….…..10 9. Контрольное домашнее задание ……………………………………….…..10 9.1. Задача №1. Распознавание с помощью метода Байеса …………….…..11 9.2. Задания к задаче №1 ………………………………………………………16 9.3. Задача №2. Диагностирование объектов с использованием методов статистических решений ……………………………………………………...22 9.4. Задания к задача №2 ………………………………………………….......26 9.5. Задача №3.Решение задач прогнозирования состояния объекта ……..30 9.6. Задания к задаче №3 ………………………………………………………35 Приложение 1 ……………………………………………………………….…39
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 810; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.233.72 (0.064 с.) |
 и среднеквадратическое отклонение
и среднеквадратическое отклонение  .
. на заданном интервале наработки Δt.
на заданном интервале наработки Δt.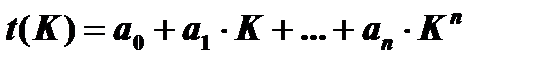 ,
,
 получим систему n +1 линейных алгебраических уравнений
получим систему n +1 линейных алгебраических уравнений (3.1)
(3.1)
 (3.2)
(3.2) (3.3)
(3.3) - средние значения К и t
- средние значения К и t (3.5)
(3.5)
 ,
, - соответственно текущее и среднее значение времени выбега, с;
- соответственно текущее и среднее значение времени выбега, с; ,
,  - соответственно текущее и среднее значение наработки, ч;
- соответственно текущее и среднее значение наработки, ч; =4250, а
=4250, а 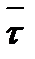 =47, общее число точек N =84 (рис. 9.2).
=47, общее число точек N =84 (рис. 9.2).


 Рис. 9.4. К построению исходного распределения случайного значения диагностического параметра
Рис. 9.4. К построению исходного распределения случайного значения диагностического параметра




