
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предикаты. Операции над предикатами.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Предикатом называется любое выражение содерж переменную при подстановке значений которых оно обращается в высказывание которое принимает значение 0 или 1. Множество различных наборов значений входящих в предикаты называют областью определения предиката. Предикат принимает значение: 1) Тождеств истинно – это предикат который принимает значение 1 при любых наборах значений входящих в него переменных. 2) Тожд ложн – это предикат который принимает значение 0 при любых наборах значений входящих в него переменных. 3) Выполнимый – это предикат который принимает значение 1 хотя бы на одном наборе значений входящих в него переменных.end Множество значений на которых предикат равен 1 назыв областью определения истинности предиката. Предикаты называютcя равносильными если они принимают одинаковое значение при соответствующих значениях переменных. Над предикатами можно выполнять все действия что и над функциями. (отриц, \/.,/\, =>, <=>) Конъюнкция двух предикатов тождественно истинна тогда и только тогда, когда оба данных предиката тождественно истинны.(остальные операции аналогично) Квантор существования можно применять к многомерным предикатам. Однократное применение квантора к одной из n переменных а- мерного предиката порождает (n-1) - мерный предикат. Пусть А(х,у)=(х+у > 1) двухместный предикат определённый на множестве R. Тогда из него связыванием переменных х и у можно получить восемь высказываний: 1 " х " у(х + у > 2) – “Для всяких действительных чисел х и у их сумма больше двух”. 2 " у " х(х + у > 2) – “Для всяких действительных чисел у и х их сумма больше двух”. 3 $ х $ у(х + у > 2) – “Существуют действительные числа х и у, сумма которых больше двух”. 4 $ у $ х(х + у > 2) – “Существуют действительные числа у и х, сумма которых больше двух”. 5 " х $ у(х + у > 2) – “Для всякого действительного числа х существует действительное число у, что их сумма больше двух”. 6 " у $ х(х + у > 2) – “Для всякого действительного числа у существует действительное число х, что их сумма больше двух”. 7 $ х " у (х+у>2) – “Существует действительное число х, что для всякого действительного числа у их сумма больше двух ”. 8 х (х+у>2) – “Существует действительное число у, что для всякого
действительного числа х их сумма больше двух ”. Законы де Моргана для кванторов 1) 2) Законы пронесения кванторов через конъюнкцию 1 ) 2) Законы пронесения кванторов через дизъюнкцию 1 ) 2 ) Законы пронесения кванторов через импликацию 1) 2) 3) 4) Законы коммутативности для кванторов 1) 2) Машина Тьюринга
Машина Тьюринга есть математическая (вообразимая) машина, а не машина физическая. Машина Тьюринга состоит из ленты, управляющего устройства и считывающей головки. Лента разбита на ячейки. Во всякой ячейке в каждый момент времени находится в точности один символ из внешнего алфавита А={а0,а1,…аn-1 }, n Управляющее устройство в каждый момент времени находит в некотором состоянии qi, принадлежащее множеству Q{q0,q1,…,qr-1}, r 1) qi aj →qk ae; 2) qi aj →qk ae R; 3) qi aj →qk ae L. Команда 1 заключается в том, что содержимое aj обозреваемой на ленте ячейки стирается, а на его место дописывается символ ae (который может совпадать с aj), машина переходит в новое состояние qk (оно может совпадать с предыдущим состоянием qi). Команда 2 работает аналогично команде 1, и дополнительно сдвигает считывающую головку в соседнюю справа ячейку.Команда 3 работает аналогично команде 1, и дополнительно сдвигает считывающую головку в соседнюю слева ячейку. Если считывающая головка находится в крайней справа (слева) ячейки ленты и происходит ее сдвиг вправо (влево), то к ленте пристраивается новая ячейка в пустом состоянии. Машинным словом или конфигурацией называется слово вида
Если машина Тьюринга выходит на заключительное состояние, то она называется остановившейся.
Функция называется вычислимой по Тьюрингу, если существует ма-шина Тьюринга, вычисляющая её.
Композиция машины Тьюринга Поскольку машина Тьюринга—алгоритм, то операции композиции применимы и к машинам Тьюринга. Рассмотрим основные из них, а именно: произведение, возве-дение в степень, итерацию.
Тезис Тьюринга. Для нахождения значений функции, заданной в некотором алфавите, тогда и только тогда существует какой нибудь алгоритм, когда функция явл вычислимой по Тьюрингу то есть когда она может вычисляться на подходящей машине Тьюрингаю. Классы рекурсивных функций В дальнейшем под множеством натуральных чисел N будем понимать множество N = {0,1,2,…,k,…} Пусть y = f(x1, x2,…, xn) – функция от n переменных. Обозначим D(y) – область определения функции y = f(x1, x2,…, xn), E(y) – область значений функции y = f(x1, x2,…, xn). Функция y = f(x1, x2,…, xn) называется числовой функцией, если: 1) D(y)=N ×∙ N ∙× …×∙ N = 2) E(y) Функция y = f(x1, x2,…, xn) называется частично числовой функцией, если: 1) D(y) 2) E(y) Следующие числовые функции мы будем называть простейшими: 1) O(x) = 0 – нуль-функция 2) 3) S(x) = x+1 – функция следования. Определим следующие три операции: суперпозиции, примитивной рекурсии и минимизации. Операция суперпозиции Будем говорить, что n – местная функция φ получается из m – местной функции ψ и n – местныхфункций f1,f2,…,fm с помощью операции суперпозиции, если для всех x1,x2,…,xn справедливо равенство: φ (x1,x2,…,xn) = ψ(f1(x1, x2,…, xn),…, fm(x1, x2,…, xn))
|
||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 851; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.218.103 (0.008 с.) |

 ;
; ;
; x(A (x) ·B (x))=(
x(A (x) ·B (x))=( x (A (x)· P)=(
x (A (x)· P)=( =
=  ;
; =
=  ;
; =
=  ;
; =
=  ;
; =
=  ;
; =
=  ;
; =
=  ;
; .
.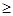 2. Некоторый символ алфавита А называется пустым, любая ячейка, содержащая в данный момент пустой символ, называется пустой ячейкой.
2. Некоторый символ алфавита А называется пустым, любая ячейка, содержащая в данный момент пустой символ, называется пустой ячейкой.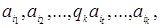 где
где 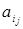
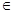 А, qk
А, qk 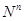 ;
;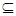 N
N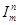 (x1, x2,…, xn) = xm, 1 ≤ m ≤ n – функция повторяющая значение своих аргументов;
(x1, x2,…, xn) = xm, 1 ≤ m ≤ n – функция повторяющая значение своих аргументов;


