
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функции алгебры логики. Булевы функции.Содержание книги
Поиск на нашем сайте Функции алгебры логики. Булевы функции. Функцией алгебры логики Теорема 1 Имеется точно В алгебре логики особое значение имеют следующие булевы функции, которые называют элементарными булевыми функциями: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) Переменная xi в функции называется фиктивной, если = при любых значениях остальных переменных. В этом случае функция, по существу, зависит от (n-1) – переменной, т.е. представляет собой функцию от (n-1) переменной. Говорят, что функция g получается из функции f удалением фиктивной переменной, а функция f получается из g введением фиктивной переменной, причем эти функции являются равными. Равносильные формулы. Формулы алг логики Приведем определение формулы алгебры логики. 1) каждая «элементарная» булева функция – формула; 2) если некоторое выражение N есть формула, то 3) если некоторые выражения M и N есть формулы, то выражения 4) других формул, кроме построенных по п.п.1), 2), 3), нет. Две формулы N и M называются равносильными, если они определяют одну и ту же булеву функцию (запись N = M будет означать, что формулы N и M равносильны) Очевидно, что отношение равносильности формул алгебры логики является: 1) рефлексивным, т.е. N = N для любой формулы N; 2) симметричным, т.е. если N = M, то M = N для любых формул N и M; 3) транзитивным, т.е. если N = M и M = J, то N = J для любых формул N,M,J. Законы алгебры логики 1) 2) Назовем формулу алгебры логики
Множество булевых функций, рассматриваемое вместе с операциями отрицания, конъюнкции и дизъюнкции, называют булевой алгеброй. Теорема 1 Если формулы алгебры логики N и M равносильны, то и двойственные им формулы N* и M* равносильны. НОРМАЛЬНЫЕ ФОРМЫ Пусть G – параметр, равный 0 или 1. Введем обозначение:
Проверкой легко установить, что x G = 1, тогда и только тогда, когда Теорема 1 Всякая булева функция f(x1,x2,…,xn) может быть представлена в следующей форме:
где 1 ≤ k ≤ n, в дизъюнкции берется по всем наборам значений переменных. Разложением функции по всем переменным называется совершенной дизъюнктивной нормальной формой (сокращенная запись СДНФ) функции. Для того что бы построить СДНФ необходимо: Для каждой такой строки образуем конъюнкцию и затем все полученные конъюнкции соединяем знаком дизъюнкции. Формула вида Теорема 3 Для любой формулы алгебры логики существует равносильная ей дизъюнктивная нормальная форма. Форма вида Теорема 4 Для любой формулы алгебры логики существует равносильная ей конъюнктивная нормальная форма. Формула алгебры логики называется тождественно истинной, если она при всех значениях входящих в нее переменных принимает значение истинно. Формула алгебры логики называется выполнимой, если она при некоторых значениях, входящих в нее переменных, принимает значение истинно. Теорема 4 Формула алгебры логики тогда и только тогда является тождественно истинной, когда каждая дизъюнкция в ее конъюнктивной нормальной форме содержит некоторую переменную вместе с ее отрицанием. Теорема 5 Формула алгебры логики тогда и только тогда является тождественно ложной, когда каждая конъюнкция в ее дизъюнктивной форме содержит некоторую переменную вместе с ее отрицанием. Метод Блейка Метод Блейка для построения сокращенной ДНФ из произвольной ДНФ состоит в применении правил обобщенного склеивания и поглощения. Подразумевается, что правила применяются слева направо. На первом этапе производится операция обобщенного склеивания до тех пор, пока это возможно. На втором производится операция поглощения. 1. Метод Блейка состоит в применении двух правил: а) обобщенное склеивание – первое правило. С помощью формулы б) поглощение – второе правило. Оно основано на равенстве
Находим в Д.Н.Ф. конъюнкции с минимальным числом сомножителей и все конъюнкции, их содержащие, вычеркиваем. Пример: Разумно в Д.Н.Ф. сначала применить метод группировки (как более простой), а затем метод Блейка. Построение минимального ДНФ ДНФ назыв минимальной, если она включает минимальное число символов по сравнению со всеми другими эквивалентами ей ДНФ Теорема 3 Минимальная ДНФ булевой функции получается из сокращенной ДНФ данной функции путем удаления некоторых элементарных конъюнкций. Следует отметить, что сокращенная ДНФ в большинстве случаев допускает дальнейшие упрощения за счет того, что некоторые элементарные конъюнкции могут поглощаться дизъюнкциями других элементарных конъюнкций. В сокращенной ДНФ элементарная конъюнкция Называется неприводимым, если после удаления из него любого интервала оно перестает быть покрытием. ДНФ булевой функции Теорема 5 Всякая минимальная ДНФ является тупиковой. 1 Выделяются все максимальные интервалы, и строится сокращенная ДНФ. 2 Строятся все тупиковые ДНФ. 3 Среди всех тупиковых ДНФ выделяются все минимальные ДНФ. Дальнейший алгоритм удобно реализовать методом импликантных матриц. Для булевой функции Для каждой Клетку импликантной матрицы, образованную пересечением i -строки и j -столбца отметим крестиком. Чтобы получить минимальную ДНФ заданной функции, достаточно найти минимальное число
Машина Тьюринга
Машина Тьюринга есть математическая (вообразимая) машина, а не машина физическая. Машина Тьюринга состоит из ленты, управляющего устройства и считывающей головки. Лента разбита на ячейки. Во всякой ячейке в каждый момент времени находится в точности один символ из внешнего алфавита А={а0,а1,…аn-1 }, n Управляющее устройство в каждый момент времени находит в некотором состоянии qi, принадлежащее множеству Q{q0,q1,…,qr-1}, r 1) qi aj →qk ae; 2) qi aj →qk ae R; 3) qi aj →qk ae L. Команда 1 заключается в том, что содержимое aj обозреваемой на ленте ячейки стирается, а на его место дописывается символ ae (который может совпадать с aj), машина переходит в новое состояние qk (оно может совпадать с предыдущим состоянием qi). Команда 2 работает аналогично команде 1, и дополнительно сдвигает считывающую головку в соседнюю справа ячейку.Команда 3 работает аналогично команде 1, и дополнительно сдвигает считывающую головку в соседнюю слева ячейку. Если считывающая головка находится в крайней справа (слева) ячейки ленты и происходит ее сдвиг вправо (влево), то к ленте пристраивается новая ячейка в пустом состоянии. Машинным словом или конфигурацией называется слово вида
Если машина Тьюринга выходит на заключительное состояние, то она называется остановившейся.
Функция называется вычислимой по Тьюрингу, если существует ма-шина Тьюринга, вычисляющая её.
Композиция машины Тьюринга Поскольку машина Тьюринга—алгоритм, то операции композиции применимы и к машинам Тьюринга. Рассмотрим основные из них, а именно: произведение, возве-дение в степень, итерацию. Тезис Тьюринга. Для нахождения значений функции, заданной в некотором алфавите, тогда и только тогда существует какой нибудь алгоритм, когда функция явл вычислимой по Тьюрингу то есть когда она может вычисляться на подходящей машине Тьюрингаю. Классы рекурсивных функций В дальнейшем под множеством натуральных чисел N будем понимать множество N = {0,1,2,…,k,…} Пусть y = f(x1, x2,…, xn) – функция от n переменных. Обозначим D(y) – область определения функции y = f(x1, x2,…, xn), E(y) – область значений функции y = f(x1, x2,…, xn). Функция y = f(x1, x2,…, xn) называется числовой функцией, если: 1) D(y)=N ×∙ N ∙× …×∙ N = 2) E(y) Функция y = f(x1, x2,…, xn) называется частично числовой функцией, если: 1) D(y) 2) E(y) Следующие числовые функции мы будем называть простейшими: 1) O(x) = 0 – нуль-функция 2) 3) S(x) = x+1 – функция следования. Определим следующие три операции: суперпозиции, примитивной рекурсии и минимизации. Операция суперпозиции Будем говорить, что n – местная функция φ получается из m – местной функции ψ и n – местныхфункций f1,f2,…,fm с помощью операции суперпозиции, если для всех x1,x2,…,xn справедливо равенство: φ (x1,x2,…,xn) = ψ(f1(x1, x2,…, xn),…, fm(x1, x2,…, xn)) Функции алгебры логики. Булевы функции. Функцией алгебры логики Теорема 1 Имеется точно В алгебре логики особое значение имеют следующие булевы функции, которые называют элементарными булевыми функциями: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) Переменная xi в функции называется фиктивной, если = при любых значениях остальных переменных. В этом случае функция, по существу, зависит от (n-1) – переменной, т.е. представляет собой функцию от (n-1) переменной. Говорят, что функция g получается из функции f удалением фиктивной переменной, а функция f получается из g введением фиктивной переменной, причем эти функции являются равными.
|
||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 313; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

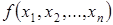 от переменных
от переменных 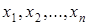 называется функция, принимающая значения 1, 0 и аргументы которой также принимают значения 1, 0.
называется функция, принимающая значения 1, 0 и аргументы которой также принимают значения 1, 0.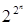 булевых функций от
булевых функций от 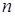 переменных.
переменных.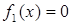 – константа 0;
– константа 0;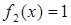 – константа 1;
– константа 1;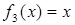 – тождественная функция;
– тождественная функция;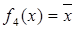 – отрицание х;
– отрицание х;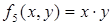 – конъюнкция x и y;
– конъюнкция x и y;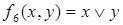 – дизъюнкция х и у;
– дизъюнкция х и у; – импликация х и у;
– импликация х и у;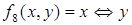 – эквивалентность х и у;
– эквивалентность х и у;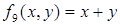 – сложение х и у по mod2;
– сложение х и у по mod2;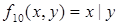 – функция Шеффера;
– функция Шеффера;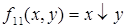 – стрелка Пирса.
– стрелка Пирса. тоже формула;
тоже формула; ,
, 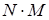 ,
, 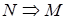 ,
, 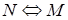 тоже формулы;
тоже формулы;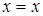 – закон тождества;
– закон тождества;  – закон противоречия;
– закон противоречия;  – закон исключительного третьего;
– закон исключительного третьего; 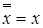 – закон двойного отрицания;
– закон двойного отрицания; 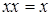 ,
, 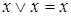 – законы идемпотентности;
– законы идемпотентности; 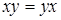 ,
, 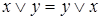 – законы коммутативности;
– законы коммутативности; 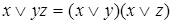 ,
, 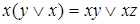 – законы дистрибутивности;
– законы дистрибутивности; 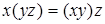 ,
, 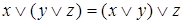 – законы ассоциативности;
– законы ассоциативности;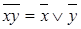 ,
,  – законы де Моргана;
– законы де Моргана;  ,
, 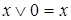 ,
, 
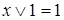 ,
, 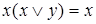 ,
, 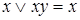 – законы поглощения;
– законы поглощения; 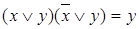 ,
, 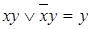 – законы склеивания.
– законы склеивания.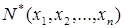 двойственной к формуле
двойственной к формуле  , если
, если 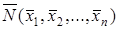 .
.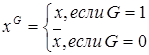
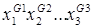 равна 1 (здесь G равен 0 или 1) тогда и только тогда, когда
равна 1 (здесь G равен 0 или 1) тогда и только тогда, когда 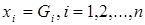 . Например, конъюнкция
. Например, конъюнкция 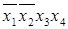 (в которой G2 = G1 = 0, G3 = G4 = 1) равна 1 только в случае, когда x 1 = x 2 = 0, x 3 = x 4 = 1.
(в которой G2 = G1 = 0, G3 = G4 = 1) равна 1 только в случае, когда x 1 = x 2 = 0, x 3 = x 4 = 1.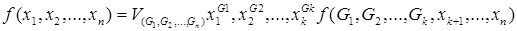 , (3.1)
, (3.1)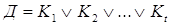 (краткая запись
(краткая запись 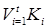 ), где
), где 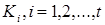 – конъюнкции
– конъюнкции 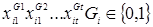 называется дизъюнктивной нормальной формой (ДНФ).
называется дизъюнктивной нормальной формой (ДНФ). (краткая запись
(краткая запись 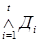 ), где
), где 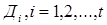 - дизъюнкции
- дизъюнкции 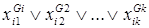 называется конъюнктивной нормальной формой (КНФ).
называется конъюнктивной нормальной формой (КНФ).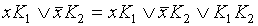 производим операцию обобщенного склеивания в Д.Н.Ф. пока это возможно. Для этого в Д.Н.Ф. отыскиваем подформулы вида
производим операцию обобщенного склеивания в Д.Н.Ф. пока это возможно. Для этого в Д.Н.Ф. отыскиваем подформулы вида 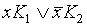 и добавляем к ним
и добавляем к ним 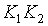 . На этом этапе формула усложняется.
. На этом этапе формула усложняется.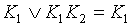 .
. .
.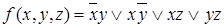
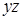 поглощается дизъюнкцией остальных элементарных конъюнкций, т.е.
поглощается дизъюнкцией остальных элементарных конъюнкций, т.е. 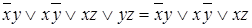 .
. , соответствующая неприводимому покрытию, называется тупиковой.
, соответствующая неприводимому покрытию, называется тупиковой. находим сокращенную ДНФ
находим сокращенную ДНФ 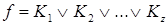 . Построим для этой функции импликантную матрицу, представляющую собой таблицу, в вертикальные входы которой записываются
. Построим для этой функции импликантную матрицу, представляющую собой таблицу, в вертикальные входы которой записываются 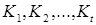 , а в горизонтальные
, а в горизонтальные  .
. находим набор
находим набор 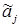 такой, что
такой, что  .
.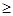 2. Некоторый символ алфавита А называется пустым, любая ячейка, содержащая в данный момент пустой символ, называется пустой ячейкой.
2. Некоторый символ алфавита А называется пустым, любая ячейка, содержащая в данный момент пустой символ, называется пустой ячейкой.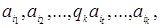 где
где 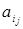
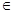 А, qk
А, qk 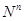 ;
;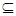 N
N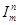 (x1, x2,…, xn) = xm, 1 ≤ m ≤ n – функция повторяющая значение своих аргументов;
(x1, x2,…, xn) = xm, 1 ≤ m ≤ n – функция повторяющая значение своих аргументов;


