
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрическая интерпретация. Минимизация Б Ф
Число различных ДНФ, составленных из переменных Конъюнкция Рангом элементарной конъюнкции назыв число переменных входящих в нее. Рассмотрим геометрическую интерпретацию задачи минимизации булевых функций. Обозначим через Свойства: 1) булевой функции 2) булевой функции 3) булевой функции Пусть Б Ф задана ДНФ К1 \/ К2\/ … \/Кi Кi – элементарные кон-ии. Множество Ni называется интервалами этого ранга если оно соответствует некоторой элементарной конъюнкции этого ранга, тогда Nf есть объединения всех интервалов которые соответствуют конъюнкциям входящим в ДНФ. Множество всех таких интервалов называется покрытием функции, т е для функции f = K1\/K2\/…\/Ki покрытие будет состоять из интервалов N1, N2,…,Ni. Таким образом если каждый интервал имеет свой ранг, то задача минимизации бул ф в интерпретации сводится к построению покрытия интервалами сумм рангов которых наименьшая. Интервалами Nk назыв макс если он не содержится ни в каком др интервале. Таким образом выбрав все макс интервалы из множества Nf и объединив их получим покрытие которое будет соответствовать сокр ДНФ Теорема 1 Если в произвольной ДНФ булевой функции f произвести все возможные обобщения склеивания и устранить затем все элементарные поглощения, то в результате получится сокращенная ДНФ функции f. Теорема 2 Если в произвольной КНФ булевой функции раскрыть все скобки в соответствии с дистрибутивным законом и устранить все элементарные поглощения, то в результате получится сокращенная ДНФ этой функции. Теорема 3 Минимальная ДНФ булевой функции получается из сокращенной ДНФ данной функции путем удаления некоторых элементарных конъюнкций. Теорема 4 Сокращенная ДНФ монотонной булевой функции не содержит отрицаний переменных и является минимальной ДНФ этой функции. Покрытие области истинности булевой функции максимальными интервалами называется неприводимым, если после удаления из него любого интервала оно перестает быть покрытием. ДНФ булевой функции
Теорема 5 Всякая минимальная ДНФ является тупиковой. 1 Выделяются все максимальные интервалы, и строится сокращенная ДНФ. 2 Строятся все тупиковые ДНФ. 3 Среди всех тупиковых ДНФ выделяются все минимальные ДНФ.
Метод Блейка Метод Блейка для построения сокращенной ДНФ из произвольной ДНФ состоит в применении правил обобщенного склеивания и поглощения. Подразумевается, что правила применяются слева направо. На первом этапе производится операция обобщенного склеивания до тех пор, пока это возможно. На втором производится операция поглощения. 1. Метод Блейка состоит в применении двух правил: а) обобщенное склеивание – первое правило. С помощью формулы б) поглощение – второе правило. Оно основано на равенстве
Находим в Д.Н.Ф. конъюнкции с минимальным числом сомножителей и все конъюнкции, их содержащие, вычеркиваем. Пример: Разумно в Д.Н.Ф. сначала применить метод группировки (как более простой), а затем метод Блейка. Построение минимального ДНФ ДНФ назыв минимальной, если она включает минимальное число символов по сравнению со всеми другими эквивалентами ей ДНФ Теорема 3 Минимальная ДНФ булевой функции получается из сокращенной ДНФ данной функции путем удаления некоторых элементарных конъюнкций. Следует отметить, что сокращенная ДНФ в большинстве случаев допускает дальнейшие упрощения за счет того, что некоторые элементарные конъюнкции могут поглощаться дизъюнкциями других элементарных конъюнкций. В сокращенной ДНФ элементарная конъюнкция Называется неприводимым, если после удаления из него любого интервала оно перестает быть покрытием. ДНФ булевой функции Теорема 5 Всякая минимальная ДНФ является тупиковой. 1 Выделяются все максимальные интервалы, и строится сокращенная ДНФ. 2 Строятся все тупиковые ДНФ.
3 Среди всех тупиковых ДНФ выделяются все минимальные ДНФ. Дальнейший алгоритм удобно реализовать методом импликантных матриц. Для булевой функции Для каждой Клетку импликантной матрицы, образованную пересечением i -строки и j -столбца отметим крестиком. Чтобы получить минимальную ДНФ заданной функции, достаточно найти минимальное число
|
||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 279; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.212.99 (0.007 с.) |
 , равно
, равно  .
. называется элементарной, если
называется элементарной, если  при
при  .
. множество всех вершин единичного n-мерного куба.
множество всех вершин единичного n-мерного куба. соответствует подмножество
соответствует подмножество  ;
; соответствует подмножество
соответствует подмножество  ;
; соответствует подмножество
соответствует подмножество  .
.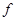 , соответствующая неприводимому покрытию, называется тупиковой.
, соответствующая неприводимому покрытию, называется тупиковой.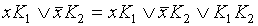 производим операцию обобщенного склеивания в Д.Н.Ф. пока это возможно. Для этого в Д.Н.Ф. отыскиваем подформулы вида
производим операцию обобщенного склеивания в Д.Н.Ф. пока это возможно. Для этого в Д.Н.Ф. отыскиваем подформулы вида 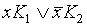 и добавляем к ним
и добавляем к ним 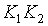 . На этом этапе формула усложняется.
. На этом этапе формула усложняется.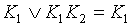 .
. .
.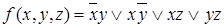
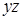 поглощается дизъюнкцией остальных элементарных конъюнкций, т.е.
поглощается дизъюнкцией остальных элементарных конъюнкций, т.е. 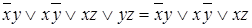 .
.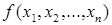 находим сокращенную ДНФ
находим сокращенную ДНФ 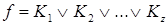 . Построим для этой функции импликантную матрицу, представляющую собой таблицу, в вертикальные входы которой записываются
. Построим для этой функции импликантную матрицу, представляющую собой таблицу, в вертикальные входы которой записываются 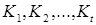 , а в горизонтальные
, а в горизонтальные  .
. находим набор
находим набор 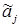 такой, что
такой, что  .
.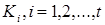 , которое совместно накрывают крестиками все столбцы импликантной матрицы.
, которое совместно накрывают крестиками все столбцы импликантной матрицы.


