
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Скорости и ускорения точек тела при свободном движенииСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте 4.11. Теорема. Вектор скорости произвольной точки
Доказательство. Движение произвольной точки
Окончательно:
Что и требовалось доказать. Теорема Ривальса для свободного движения тела. Вектор полного ускорения любой точки твердого тела при его свободном движении равен геометрической сумме вектора ускорения полюса, вектора осестремительного и вектора вращательного ускорений.
где Доказательство. Продифференцируем (4.19) по времени. С учетом формулы (4.3) получим:
Или с учетом (4.18)
Вопросы для самоконтроля к главе 4 1.Какое движение твердого тела называется сферическим? 2. Запишите уравнения сферического движения тела. 3. Опишите механизм сферического движения твердого тела. 4. Что называется мгновенной осью вращения и мгновенной угловой скоростью вращения тела при сферическом движении? 5. Запишите формулу для вектора линейной скорости точки тела, совершающего сферическое движение. 6. Как направлен вектор линейной скорости точки при сферическом движении тела? 7. Запишите формулу для вектора линейного ускорения точки тела, совершающего сферическое движение. 8. Как направлены векторы вращательного и осестремительного ускорений точки при сферическом движении? 9. Какое движение твердого тела называется свободным? 10. Запишите уравнения свободного движения тела. 11. Проанализируйте уравнения свободного движения тела и опишите механизм свободного движения твердого тела. 13. Что называется вектором мгновенной угловой скорости и мгновенного углового ускорения тела при его свободном движении? 13. Запишите формулу для вектора скорости произвольной точки тела, совершающего свободное движение. 14. Сформулируйте теорему Ривальса об ускорении точки при свободном движении тела.
|
||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 467; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

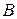 тела равен геометрической сумме вектора скорости полюса и вектора скорости точки в сферическом движении тела вокруг полюса.
тела равен геометрической сумме вектора скорости полюса и вектора скорости точки в сферическом движении тела вокруг полюса. или
или  (4.18)
(4.18) (рис.4.6). Тогда
(рис.4.6). Тогда  . Продифференцируем последнее равенство по времени.
. Продифференцируем последнее равенство по времени.  или
или 
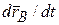 - вектор скорости точки
- вектор скорости точки  ,
, 
 - вектор скорости полюса
- вектор скорости полюса 
 - вектор скорости точки
- вектор скорости точки 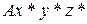 , то есть вектор скорости точки в её сферическом движении относительно полюса
, то есть вектор скорости точки в её сферическом движении относительно полюса  , так как тело абсолютно твердое. Но
, так как тело абсолютно твердое. Но  - радиус - вектор с началом в полюсе
- радиус - вектор с началом в полюсе  известны, то c учетом формулы Эйлера (4.4) имеем:
известны, то c учетом формулы Эйлера (4.4) имеем: . (4.18)
. (4.18) или
или 
 , (4.20)
, (4.20) ,
,  (4.21)
(4.21)



