
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функционально полные системы логических функций
Любую логическую функцию f двоичных переменных х1, х2,..., хп можно вычислить путем использования логических операций И, ИЛИ и НЕ. С помощью электронных элементов И, ИЛИ и НЕ можно построить функциональную схему, реализующую любую логическую функцию. Очевидно, что набор функций (И, ИЛИ, НЕ) является функционально полным. Набор физических (электронных) элементов, реализующих эти три операции, образует функционально полную систему логических элементов. Свойствами функциональной полноты обладают также наборы (И, НЕ) и (ИЛИ, НЕ). Действительно, в наборе (И, НЕ) функцию ИЛИ можно выполнить через операции И, НЕ путем эквивалентного преобразования f = х1 + х2 = В наборе (ИЛИ, НЕ) функцию И можно выполнить через операции ИЛИ и НЕ следующим образом: f = х1 + х2 = Таким образом, набор функций (И, ИЛИ, НЕ) обладает избыточностью. Функционально полными являются функции И—НЕ, ИЛИ—НЕ. Имея необходимое количество логических элементов И—НЕ либо ИЛИ—НЕ с требуемым числом входов, можно реализовать (т. е. построить функциональную схему) любую логическую функцию. Для вычисления переключательной функции путем выполнения операции И—НЕ ее необходимо вначале представить в ДНФ. Выполнив далее двойное отрицание и применив закон отрицания, мы приведем ЛФ к требуемому виду. Например, ЛФ f = f = По этому выражению логическая функция реализуется на элементах И—НЕ в соответствии с рис. 3.8.
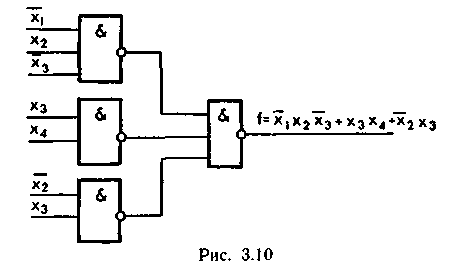
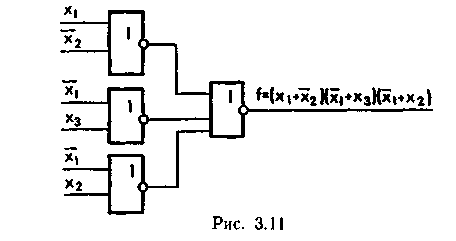
Рисунок 3.8 Для реализации ЛФ в базисе ИЛИ—НЕ необходимо записать её сначало в КНФ. Выполнив далее двойное отрицание и применив закон отрицания, получим искомую форму. Например, ЛФ f = (х1+ f = По этому выражению логическая функция реализуется на элементах ИЛИ—НЕ в соответствии с рис. 3.9.
Рисунок 3.9
3.3.1 Метод непосредственных преобразований Метод Карно-Вейча Логическую схему, которая реализует заданный алгоритм преобразования сигналов, можно синтезировать непосредственно по выражению, представленному в виде СДНФ или СКНФ. Тем не менее, полученная при этом схема, как правило, не оптимальна с точки зрения ее практической реализации. Поэтому исходную логическую функцию обычно минимизируют.
Минимизация логических функций есть нахождение их выражений с минимальным числом букв. Целью минимизации логической функции является построение экономичных схем компьютеров и уменьшение стоимости её технической реализации. Критерий, соответственно которому выполняется минимизация, далеко не однозначный и зависит как от типа задачи, так и уровня развития технологии. Основные требования к задаче синтеза: минимальное число элементарных конъюнкций или дизъюнкций в логической формуле и однородность используемых операций. Кроме требований минимизации ставится ряд ограничений и условий на выбор элементной базы для синтезированного устройства. Для минимизации логических функций используют два основных метода: метод Квайка –метод непосредственного преобразования и метод карт Карно (диаграмм Вейча). 3.3.1 Метод непосредственных преобразований Одним из простейших методов минимизации является метод непосредственных преобразований, который применяется с использованием основных теорем алгебры логики.
Непосредственное упрощение исходной логической функции, заданной в виде СДНФ, выполняется в следующем порядке: 1. Для каждой из возможных пар соседних конституант СДНФ применяется операция полного склеивания. При этом из них исключается по одной переменной. Потом выполняется приведение подобных членов. Этот процесс повторяется до тех пор, пока в полученном выражении не останется конъюнкций, которые отличаются друг от друга значениями одной переменной. Полученная таким способом форма называется сокращенной нормальной формой. Конъюнкции, которые входят в сокращенную нормальную форму, называются простыми импликантами. Каждой логической функции отвечает лишь одна сокращенная форма. 2. Применяя к сокращенной нормальной форме операцию обобщенного склеивания, исключают из нее лишние конъюнкции (импликанты). Полученная в результате последовательного ряда таких преобразований форма, не допускающая дальнейших склеиваний, называется тупиковой формой логической функции. Тупиковых форм для одной функции может быть несколько. 3. Полученная тупиковая форма может случайно оказаться минимальной. Минимальной формой является тупиковая форма минимальной длины. В общем случае для поиска минимальной формы необходим перебор тупиковых форм, который позволяет найти одну или несколько минимальных форм логической функции. Метод Квайна применяется к функциям, заданным в СДНФ (возможно задание и в СКНФ), и проводится, как правило, в два этапа. На первом этапе выполняется переход от СДНФ к сокращенной ДНФ путем проведения всех возможных склеиваний друг с другом сначала конъюнкций ранга п, затем ранга п — 1, далее п — 2 и т. д. Каждый раз в группе конъюнкций отыскиваются пары конъюнкций вида Ах и А Например, конъюнкции
При этом получается конъюнкция А ранга п -1, а конъюнкции Ах и А Результатом выполнения последовательности попарного сравнения и склеивания конъюнкций ранга п является группа конъюнкций ранга п —1 и непомеченные конъюнкции ранга г. Непомеченные конъюнкции ранга п не участвовали в склеивании, следовательно, являются простыми импликантами и включаются в сокращенную ДНФ. Конъюнкции ранга п —1 вновь подвергаются попарному сравнению и склеиванию, как это было описано выше для конъюнкций ранга п; в результате имеем группу конъюнкций ранга п — 2 и непомеченные конъюнкции ранга п —1, которые являются простыми импликантами, включаемыми далее в сокращенную ДНФ. Первый этап заканчивается тогда, когда вновь полученная группа конъюнкций не содержит склеивающихся членов, т. е. содержит только простые импликанты. После этого записывается сокращенная ДНФ, в которую включаются все полученные простые импликанты. Рассмотрим реализацию первого этапа на примере функцииЛФ f 1 2 3 4 5 f = где для удобства последующего изложения над конъюнкциями записаны присвоенные им номера. Анализируя в выражении всевозможные пары конъюнкций 1-2, 1-3, 1-4, 1-5, 2-3, 2-4, 2-5, 3-4, 3-5, 4-5, находим, что операция склеивания выполняется между парами 1-3 по х1, 2-5 по х1, 3-4 по х3, 4-5 по х2. Таким образом, все конъюнкции исходной СДНФ участвуют в склеивании и помечаются подчеркиванием. 1 2 3 4 Теперь исходная СДНФ (3.5) записывается в виде f = Продолжая для выражения (3.6) процедуру склеивания, сравниваем попарно конъюнкции 1-2, 1-3, 1-4, 2-3, 2-4 и 3-4. Эти пары конъюнкций между собой не склеиваются. Поэтому полученная запись ЛФ (3.6) представляет собой сокращенную ДНФ исходной ЛФ (3.5), содержащей только простые импликанты. Второй этап заключается в переходе от сокращенной ДНФ к тупиковым ДНФ и выборе среди них МДНФ. Тупиковой называется такая ДНФ, среди простых импликант которой нет ни одной лишней. При этом под лишней понимается такая простая импликанта, удаление которой не влияет на значение истинности этой функции. Возможны случаи, когда в сокращенной форме нет лишних простых импликант. Тогда сокращенная ДНФ является тупиковой.
Для выявления лишних простых импликант строится импликантная матрица, которая называется также матрицей (таблицей) покрытий. Каждая строка импликантной матрицы соответствует одной простой импликанте, а столбцы — конституантам единицы, которыми они и помечаются. Для рассматриваемого примера импликантная матрица приведена в табл. 3.14.
Нахождение тупиковых ДНФ по импликантой матрице начинается с разметки матрицы. При этом каждая импликанта сравнивается со всеми конституантами единицы. Если импликанта является собственной частью некоторой конституанты, то на пересечении строки и столбца ставится условный знак, например – плюс (+). Конституенты единицы, помеченные в строке с простой импликантой, поглощаются (покрываются) этой простой импликантой. Это значит, что на соответствующих наборах данная импликанта обеспечивает единичные значения ЛФ. Например, простая импликанта Выявление лишних простых импликант выполняется следующим образом: -В импликантной таблице условно вычеркивается строка с проверяемой простой импликантой вместе с соответствующими пометками в строке. -Если при этом окажется, что в каждом столбце импликантной таблицы остается, хотя бы по одной пометке, проверяемая импликанта является лишней и ее следует удалить. -Оставшиеся простые импликанты покрывают все единичные значения ЛФ. -Испытание каждой последующей простой импликанты возможно лишь после удаления уже выявленных лишних простых импликант. -Изменение последовательности испытаний и удаления лишних членов сокращенной ДНФ может привести к различным тупиковым формам ЛФ, из которых выбирается МДНФ. Из табл. 3.13 видно, что только простая импликанта 1 обеспечивает единичное значение ЛФ на наборе 000, а импликанта 2 — на наборе 011 (соответствующие этим наборам столбцы обозначены конституантами единицы Простую импликанту 3 можно считать лишней. Однако, если ее сохранить, лишней можно считать простую импликанту 4. Таким образом, для ЛФ возможны две тупиковые формы: f1т = в которую не включена лишняя импликанта х1 и f2т = в которую не вошла лишняя импликанта x1x3. Тупиковые формы (3.7) и (3.8) имеют одинаковое суммарное количество переменных, поэтому любую из них можно выбрать в качестве минимальной (МДНФ).
Например, можно считать fmin = f1т = Эта ЛФ реализуется схемой с ценой С = 9 (3 х 2 + 3 = 9). Пример 4. Логическую функцию F в виде СДНФ F = 1. Добавим к данной функции слагаемое х1х2 F = 2. Применим метод склеивания (правило 11) к одинаково подчеркнутым элементарным конъюнкциям (x ∙ y + Для х1 Для Для х1х2 Результат склеивания: F = х2 3. Применим тот же метод склеивания для двух последних элементарных конъюнкций: Для х1 Окончательный результат: Fmin =FT = х2 Полученная в результате минимизации логическая функция называется тупиковой. Логическая функция может иметь несколько тупиковых форм. Пример5. Найти минимальную форму функции, заданной СДНФ F(a, b,c) =а Применяя операцию полного склеивания к сочетаниям каждой конституанты со всеми соседними и приводя подобные члены, получаем сокращенную нормальную форму: F(a,b,c) =
Очевидно, что анализируемой функции отвечают две минимальных нормальных формы F2 (a,b,c) и F3 {a,b,c). Для исходной функции, заданной в виде СКНФ, минимизация методом непосредственного упрощения выполняется таким образом. 1. Сначала к членам СКНФ применяют операцию полного склеивания. 2. Пользуясь законом дистрибутивности, раскрывают скобки в полученном выражении. 3. Приводят подобные члены и применяют операцию поглощения. 4. Полученную таким способом ДНФ минимизируют в указанном выше порядке.
Метод Карно-Вейча Метод диаграмм Вейча (карт Карно) удобен для минимизации ЛФ, содержащих обычно не более пяти переменных. Метод диаграмм Вейча, усовершенствованный Карно, применяется в том случае, если число аргументов не более 5. Представляют собой определенную таблицу истинности и отличаются друг от друга способом обозначения строк и столбцов таблицы истинности. Число клеток карты Карно определяется величиной 2n, где п равняется числу входных переменных, с разметкой строк и столбцов переменными. Например, если переменных 3 (n = 3), то (23 = 8) клеток -8. Каждой комбинации переменных можно поставить в соответствие клетку карты Карно. В клетку записывается значение функции (0 или 1) для данной комбинации входных переменных. Входные переменные располагаются по внешним сторонам карты напротив ее строк и столбцов. При этом значение каждой из входных переменных относится ко всей строке или столбцу и равняется 1, если напротив строки (столбца) стоит под скобкой обозначение этой переменной; для других строк (столбцов) значение этой переменной равняется 0.
Диаграмма Вейча для двух переменных х1 и х2. Переменных -2. Число клеток: 22 = 4
Диаграмма Вейча для трех переменных х1, х2 и х3 Переменных -3. Число клеток: 23 = 8
Диаграмма Вейча для четырех переменных х1, х2, х3 и х4 Переменных -4. Число клеток: 24 = 16
Каждая из входных переменных делит по-своему любую карту Карно на две равных части, в одной из которых значение этой переменной равняется 1, а в другой 0. Для минимизации логическая функция (ЛФ) приводится к совершенной дизъюнктивной нормальной форме (СДНФ), после чего заполняется диаграмма для п переменных. При этом в соответствующую клетку диаграммы вписывается 1, если ЛФ = 1 в данном наборе. В остальные клетки вписываются 0 либо эти клетки вообще не заполняются. В заполненной диаграмме обводят прямоугольными контурами клетки с 1, после чего записывают минимизированную дизъюнктивную нормальную форму (МДНФ) логической функции в виде дизъюнкции простых импликант, описывающих эти контуры. При проведении контуров придерживаются следующих правил: -количество клеток с 1 должно выражаться величиной 2i, где i = 0, 1, 2, … (т.е. 1, 2, 4, 8 и т.д.); - 1 в крайних клетках одного столбца или одной строки могут включаться в один контур; -каждый контур должен включать как можно большее число клеток с 1, а общее число контуров должно быть как можно меньшим. В простую импликанту, описывающую контур, включаются те переменные, которые во всех клетках контура имеют либо только прямое, либо только инверсное значение. Пример 1. Минимизировать ЛФ F =
1. Заполняем диаграмму Вейча для двух переменных.
1. Проводим два контура, охватывающие клетки с единицами.
2. Находим простые импликанты описывающие контур, для чего выясняем от каких переменных не зависит данный контур. а) вертикальный контур охватывает строки с х1 и б) горизонтальный контур охватывает строки с х2 и 4. Следовательно, ЛФ будет иметь МДНФ: F = Пример 2. Минимизировать ЛФ F =х1х2+х1 1. Приводим логическую функцию к СДНФ: F = х1х2 (х3+
2. Заполняем диаграмму Вейча для трех переменных.
3. Проводим три контура, охватывающие клетки с 1. 1 контур (зеленый) –охватывает клетки х1х2х3 и х1 2 контур (красный) –охватывает клетки х1х2 3 контур (красный) –охватывает клетки х1 4. Находим простые импликанты описывающие контур, для чего выясняем от каких переменных не зависит данный контур.
5. Следовательно, ЛФ будет иметь МДНФ: F = х1х3 + х2 В этом примере вместо 1 контура можно было провести контур охватывающий конъюнкции х1х2х3 и х1х2 Карты Карно Для минимизации функции с числом переменных n ≤ 6 используют карты Карно. Число клеток карты Карно определяется величиной 2n, где п равняется числу входных переменных, с разметкой строк и столбцов переменными. Например, если переменных 3 (n = 3), то (23 = 8) значит клеток -8. Карты Карно для функции трех переменных F(х1 х2, х3) показаны на рис. 3.10. · Строки карты отмечены значениями переменной х1 , а столбцы -значениями переменных х2, х3. · Каждая клетка карты Карно однозначно соответствует одному набору таблицы истинности для функции трех переменных (рис. 3.10, а) или минтермам этой функции (рис. 3.10, б). · Клетки карты Карно часто нумеруют десятичными цифрами - номерами наборов (рис. 3.10, в). · Рисунок 3.10 – Карты Карно для функций трех переменных Например, заполнение карты Карно для функции, заданной табл. 3.12, показано на рис. 3.6, г.
Минтермы в соседних клетках карты Карно в строке (включая верхние и нижние) или в столбце (включая крайние) отличаются значением одной переменной, что позволяет выполнить операцию склеивания по этой переменной. Например, на рис. 3.6, г минтермы Аналогично для минтермов Х1 В результате минимизации функции Р(Х1 Х2, Х3) получают ее минимальное выражение Р = Перечислим общие правила минимизации.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 1668; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.12.172 (0.112 с.) |
 =
= 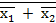

 3 + х3
3 + х3 
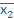
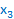 в соответствии с описанными действиями приводится к виду
в соответствии с описанными действиями приводится к виду =
= 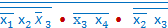
 2)(
2)( 1 + х3)(
1 + х3)(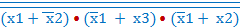 =
= 

 = 1
= 1
 = 0
= 0
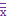 = x
= x
 =s w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:b/><w:i/><w:color w:val="7030A0"/><w:lang w:val="EN-US"/></w:rPr><m:t>x</m:t></m:r></m:e></m:bar></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
=s w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:b/><w:i/><w:color w:val="7030A0"/><w:lang w:val="EN-US"/></w:rPr><m:t>x</m:t></m:r></m:e></m:bar></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 
 ∙ y) = y
∙ y) = y
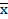 , где А — общая часть этих конъюнкций. Эти конъюнкции склеиваются между собой по переменной х
, где А — общая часть этих конъюнкций. Эти конъюнкции склеиваются между собой по переменной х +
+ 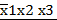 +
+ 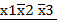 +
+ 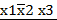 +
+ 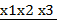 (3.5)
(3.5)


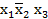

 3
3
 2
2  3 входящая в сокращенную ДНФ (3.6) рассматриваемого примера, является собственной частью конституант единиц
3 входящая в сокращенную ДНФ (3.6) рассматриваемого примера, является собственной частью конституант единиц  и
и 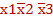 , и поэтому в строке с данной простой импликантой (табл. 3.13) поставлены две пометки X в соответствующих колонках. Аналогично размечены другие строки табл. 3.13.
, и поэтому в строке с данной простой импликантой (табл. 3.13) поставлены две пометки X в соответствующих колонках. Аналогично размечены другие строки табл. 3.13.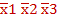 и
и 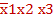 ), поэтому эти простые импликанты обязательно войдут во все тупиковые ДНФ.
), поэтому эти простые импликанты обязательно войдут во все тупиковые ДНФ. х2
х2  +х1
+х1 
 , которое уже есть в данной функции, используя правило 3 (x ∙ x = x).
, которое уже есть в данной функции, используя правило 3 (x ∙ x = x). х2
х2 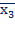 + х1
+ х1 
 ∙ y = y):
∙ y = y):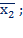
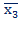 и х1х2
и х1х2 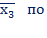 х1 -получим х2
х1 -получим х2  c +
c + 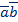 c +
c +  +
+ 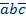 + ab
+ ab  = abc.
= abc.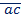 .
.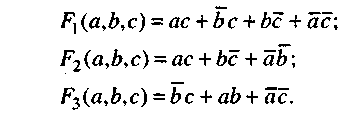 Применение операции обобщенного склеивания к импликантам можно осуществить в нескольких вариантах. Каждому из них отвечает одна из следующих тупиковых форм:
Применение операции обобщенного склеивания к импликантам можно осуществить в нескольких вариантах. Каждому из них отвечает одна из следующих тупиковых форм: х2 + х1
х2 + х1  +
+  с помощью диаграмм Вейча.
с помощью диаграмм Вейча. 1, следовательно в простую импликанту, описывающую горизонтальный контур х1 входить не будет.
1, следовательно в простую импликанту, описывающую горизонтальный контур х1 входить не будет. х3+
х3+  с помощью диаграмм Вейча.
с помощью диаграмм Вейча.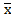 1
1
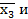

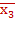
 х3
х3
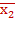 х3
х3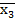 , тогда МДНФ имела бы вид: F = х1х2 + х2
, тогда МДНФ имела бы вид: F = х1х2 + х2 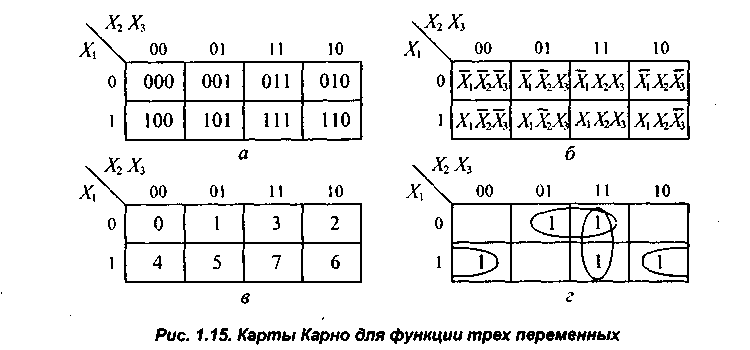 При минимизации для каждого минтерма, входящего в СДНФ функции, ставится единица, а другие клетки не заполняются.
При минимизации для каждого минтерма, входящего в СДНФ функции, ставится единица, а другие клетки не заполняются.
 X3 и
X3 и  Х2 Х3 (клетки с номерами 1 и 3) отличаются значением переменной Х2, поэтому они склеиваются по ней и представляются конъюнкцией двух переменных
Х2 Х3 (клетки с номерами 1 и 3) отличаются значением переменной Х2, поэтому они склеиваются по ней и представляются конъюнкцией двух переменных 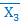 и Х1 Х2
и Х1 Х2 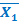 Х3 v Х2 Х3 v Х1
Х3 v Х2 Х3 v Х1  .
.


