
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дизъюнктивные формы представления ЛФСодержание книги
Поиск на нашем сайте Конъюнкция любого числа двоичных переменных х1, х2,..., хп называется элементарной, если сомножителями в ней являются либо одиночные аргументы, либо отрицания одиночных аргументов. Например, конъюнкции а конъюнкции х1 Очевидно, что символ любой переменной в элементарной конъюнкции может встречаться только один раз, так как произведение переменной на себя равно этой же переменной (по правилу повторения), а произведение переменной на свое отрицание равно нулю. Дизъюнктивной нормальной формой (ДНФ) переключательной функции называется дизъюнкция (логическая сумма) любого числа элементарных конъюнкций, в каждое из которых аргумент или его отрицание (инверсия) входит один раз. Например, ЛФ F = Число переменных, входящих в элементарную конъюнкцию, определяет ранг этой конъюнкции. Например, - - ДНФ может быть получена из таблицы истинности следующим образом: для каждого набора аргументов, на котором функция равна «1», записывают элементарные произведения переменных, причем переменные, значения которых равно нулю, записывают с инверсией. Полученные произведения, которые носят названия конституанты единиц, или минтермов, суммируют. Пример 3.4 Найти ДНФ для логической функции 3-х переменных, которая равна единице в случае, если хотя бы две из входных переменных равны 1.
· Запишем эту функцию в виде таблицы истинности: · В последнем столбце отмечаем «1» те строки, которые удовлетворяют условию задания. · Для написания ДНФ ЛЭ используем строки, логическая функция которых равна «1». · Это строки: 3, 5, 6, и 7 таблицы. · ДНФ для данной логической функции имеет вид: F (х2, х1, х0) = ДНФ, полученная суммированием конституанта единицы, называют совершенной СДНФ. Совершенной ДНФ (СДНФ) логической функцией, имеющей п аргументов, называется такая форма, в которой все конъюнкции имеют ранг п. Или совершенной (СДНФ) логической функции имеющей n аргументов (х1, х2,..., хп) называется такая форма в которой все конъюнкции содержат n аргументов. Например, ЛФ f1 = а ЛФ - f2 =
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 266; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 х2
х2  и х1
и х1 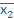 х3 являются элементарными,
х3 являются элементарными, и
и  х3 ими не являются.
х3 ими не являются.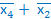 +
+  х4 записана в ДНФ, так как она представляет собой логическую сумму элементарных конъюнкций.
х4 записана в ДНФ, так как она представляет собой логическую сумму элементарных конъюнкций. х2
х2  — конъюнкции 1-го ранга;
— конъюнкции 1-го ранга; 2х1х0 + х2
2х1х0 + х2 
 +
+  х2
х2 





