
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементарные логические функции и принцип двойственности
Произвольная переключательная функция (ПФ) может быть выражена в форме функции от двоичных переменных с помощью ограниченного числа элементарных логических функций. Булевы функции одного и двух аргументов называют элементарными. Схему, которая осуществляет элементарную логическую операцию, называют логическим элементом (вентилем). Совокупность взаимозависимых логических элементов с формальными методами описания называется логической схемой. Соответственно перечню логических операций различают три основных логических элемента (ЛЭ): И, ИЛИ, НЕ. Названия и условные графические обозначения основных логических элементов, применяемых в компьютерной схемотехнике, представлены в табл. 3.8. Значения переменных (операндов) отображаются электрическими сигналами с двумя четко выраженными уровнями значений. Число входов элементов И, ИЛИ может быть произвольным, а элемент НЕ имеет всегда только один вход.
При сравнении операций И, ИЛИ можно заметить, что, если в условиях, которые определяют операцию И, значения всех переменных и самой функции заменить их инверсией, а знак логического умножения – знаком логического сложения, получим постулаты, которые определяют операцию ИЛИ: если a∙ b = c, то если a + b = c, то Это свойство взаимного преобразования постулатов операций логического сложения и умножения носит название принципа двойственности. Две функции алгебры логики называются двойственными, если одна получается из другой заменой каждой операции конъюнкции на операцию дизъюнкции и наоборот.
Нетрудно заметить, что почти все вышеприведенные законы алгебры логики (кроме 5) обладают свойством двойственности, т.е. представлены парой соотношений, каждое из которых получается заменой операции И на ИЛИ, операции ИЛИ на И, логической 1 на логический 0 и логического 0 на логическую 1.
Например, для функции 11 F (a, b) = ab + двойственной является функция F’(a, b) = (a + b)( Принцип двойственности формулируется так: если функция F1 и F2 равносильны, то и двойственные им функции F’1 и F’2 также равносильны. Необходимо отличать двойственные формы функции от инверсных функций, которые вытекают из исходных инвертированием последних. При этом не только все операции заменяются на двойственные, но и все переменные заменяются их инверсиями. Например, для функции F (a, b) = ab + инверсной будет функция F (a, b) = ab + Важным практическим следствием принципа двойственности есть тот факт, что при записи логических выражений и, значит, построении логических схем, можно обойтись только двумя типами операций: И и НЕ или ИЛИ и НЕ. Совокупность логических элементов (ЛЭ) которая позволяет реализовать логическую схему любой сложности, называется функционально полной системой. Функционально полными системами являются системы: - И и НЕ, - ИЛИ и НЕ, - И, ИЛИ, НЕ На практике широкое применение нашли ЛЭ, которые совмещают функции элементов указанных выше функционально полных систем. Это элементы И-НЕ и ИЛИ-НЕ (рис. 3.1).
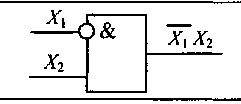
Рисунок 3.1 – Условные графические обозначения двухвходовых ЛЭ И-НЕ и ИЛИ - НЕ Если рассмотреть выполнение операций И, ИЛИ и НЕ на элементах ИЛИ-НЕ то в соответствии с принципом двойственности, если a ∙ b = c, то На рис. 3.2 приведены примеры реализации основных логических операций с использованием только элементов ИЛИ-НЕ.
Рисунок 3.3 – Реализация логических операций И, ИЛИ, НЕ на базе элементов И-НЕ
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 270; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.171.180 (0.006 с.) |








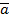 +
+ 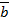 =
= 

 = 1
= 1
 = 0
= 0
 = x
= x
 =
= 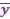
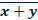 =
= 
 ∙ y = y
∙ y = y
 b
b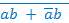 = (
= (  )(а +
)(а + 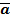 +
+  =
=  . Инвертируя правую и левую часть первого выражения, получим
. Инвертируя правую и левую часть первого выражения, получим  , т.е. логическая операция И может быть заменена операциями ИЛИ и НЕ.
, т.е. логическая операция И может быть заменена операциями ИЛИ и НЕ. На рис. 3.3 приведены примеры реализации основных логических операций с использованием только элементов И-НЕ.
На рис. 3.3 приведены примеры реализации основных логических операций с использованием только элементов И-НЕ. Рисунок 3.2 – Реализация логических операций И, ИЛИ, НЕ на базе элементов ИЛИ-НЕ
Рисунок 3.2 – Реализация логических операций И, ИЛИ, НЕ на базе элементов ИЛИ-НЕ


