
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лінійні операції над векторами: означення і властивості.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Лінійними операціями над векторами називаються операції додавання та множення вектора на число (скаляр).
Проекція вектора на вісь. Властивості проекції.
Векторною проекцією вектора Позначають: Проекцією або скалярною проекцією вектора
Властивості проекції вектора на вісь:
Напрямні косинуси вектора. Теорема про геометричний зміст координат вектора. Теорема про геометричний зміст декартових прямокутних координат. Координати вектора в ДПКС дорівнюють проекціям цього вектора на відповідні координатні осі.
6. Скалярним добутком двох векторів
враховуючи, що
то маємо геометричний зміст скалярного добутку:
Властивості скалярного добутку 2-х векторів.
Означення векторного добутку 2-х векторів. Вираз векторного добутку через координати.
Властивості векторного добутку двох векторів.
10.
11. Властивості мішаного добутку.
12.
Означення визначника n-го порядку. Формули обчислення визначників 2-го та 3-го порядку.
Властивості визначників.
Означення матриці. Нульова, одинична, діагональна матриці. Операція додавання матриць, множення матриці на число. Властивості цих операцій.
16.
Означення оберненої матриці. Критерій існування оберненої матриці. Теорема про визначник оберненої матриці. Знаходження оберненої матриці за допомогою алгебраїчних доповнень. Теорема. Якщо визначник (det A) не дорівнює нулю, то матриця А має обернену:
|
|||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 409; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.151.70 (0.01 с.) |


 - задано вектор
- задано вектор U – вісь
U – вісь
 Знайдемо проекції точок А і В на вісь U, для цього через ці точки проведемо площини α та β перпендикулярні до осі U. Таким чином проекціями точок А і В будуть точки А1 та В1.
Знайдемо проекції точок А і В на вісь U, для цього через ці точки проведемо площини α та β перпендикулярні до осі U. Таким чином проекціями точок А і В будуть точки А1 та В1.

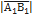 взятий зі знаком +, якщо вектор
взятий зі знаком +, якщо вектор 





 Нехай α, β та γ – це кути, які утворює вектор ā з координатними осями Ox, Oy та Oz відповідно. Тоді cosα, cosβ, cosγ називаються направними косинусами вектора ā. Згідно з попередньою теоремою:
Нехай α, β та γ – це кути, які утворює вектор ā з координатними осями Ox, Oy та Oz відповідно. Тоді cosα, cosβ, cosγ називаються направними косинусами вектора ā. Згідно з попередньою теоремою:
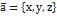






 Означення скалярного добутку 2-х векторів. Вираз скалярного добутку через координати.
Означення скалярного добутку 2-х векторів. Вираз скалярного добутку через координати. і
і  називається число
називається число  , що дорівнює добутку довжин цих векторів на косинус кута між ними. Позначають: (
, що дорівнює добутку довжин цих векторів на косинус кута між ними. Позначають: (








 Означення мішаного добутку 3-х векторів. Вираз мішаного добутку через координати.
Означення мішаного добутку 3-х векторів. Вираз мішаного добутку через координати.


 Означення перестановки, інверсії. Означення визначника n-го порядку.
Означення перестановки, інверсії. Означення визначника n-го порядку.













 Операція транспонування матриці. Операція множення матриць. Властивості цих операцій.
Операція транспонування матриці. Операція множення матриць. Властивості цих операцій. , де |А|- визначник матриці А; J- матриця яка складається з алгебраїчних доповнень Аij до елементів аij матриці А, а саме:
, де |А|- визначник матриці А; J- матриця яка складається з алгебраїчних доповнень Аij до елементів аij матриці А, а саме:




