
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Означення рангу матриці. Теорема про базисний мінор. Методи знаходження рангу. ⇐ ПредыдущаяСтр 3 из 3
Рангом матриці А- називається найвищій з порядок її мінорів відміних від 0. 19. Означення векторного простору. Множина ( L) будь-яких елементів наз. Дійсним векторним (лінійним) простором, якщо виконуються такі умови: 20. Означення лінійно – залежної, лінійно – незалежної системи векторів. Приклади Означення: лінійною комбінацією елементів а11,ах…аn векторного простору L наз сума добутків цих елементів на довільні дійсні числа, тобто L1а1 +L2a2+…+Lnan lt Li належить R.
Альфа-L=1,2,3,4,5,…. Елементи a1,a2,….,an наз. Лінійно залежними якщо існують числа L1,L2,…Ln з яких хочаб одне не дорівнює 0 і виконується рівність L1a1+L2a2+….Lnan=0
Елемети a1,a2,….,an наз. Лінійно незалежними якщо рівність виконується тільки зі такої умови L1a1+L2a2+…+Lnan=0
21. Означення базису векторного простору. Координаті вектору в заданому базисі.
Упорядкована множина елементів l 1, l 2, l n називається базисний вектор простору L, якщо виконується наступні умови:
1) L i є L, будь-яке і = 1, 2, 3,... n 2) l 1, l 2,... l n лінійно незалежні 3) для будь якого х є L знайдеться лямба 1, лямба 2,... n такі що х= лямба 1 l 1 + лямба 2 l 2 +...+ лямба n l n (розклад вектора х по базису l 1, l 2,... l n, а коефіцієнти лямба 1 лямба 2 лямба n називаються координати вектору х у базисі l 1, l 2, l 3 Покажемо що координати вектору у заданому базисі визначені однозначно 1) одним з базисів векторного простору /R є система яка складається з { l 1 =1} 2) базис векторного простору /R^n є { l 1 = (1,0), l 2 = (0,1)} 3) /R^n є l 1=(1,0,0,0...0) l 2=(0,1,0,0...0) l n=(0,0,0,0...1) 4) Rn [x]: l 1= 1 l 2= x l 3= x^2 l n= x^(n-1) l (n+1)= x^n
22. Приклади базисів. Вимірність векторного простору. Теорема про вимірність.
1. Одним з базисів векторного простору /R є система яка складается 2.Базисом векторного простору /R^2 буде упорядкована система
3./R^n 4. Базису простору M2(/R) 5.Базис простору
23. Матриця переходу від одного базису векторного простору до іншого. Властивості матриці переходу.
Матрицею переходу в оскільки
Матриця переходу це
Властивості матриці переходу. 1) Матриця переходу завжди не вироджена 2)Будь-яка не вироджена матриця є матрицею переходу від одного базису до деякого іншого.
24. Формули перетворення координат вектора при змінні базису(доведення).
Нехай
матриця переходу від першого базису до другого.
|
|||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 270; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.36.192 (0.007 с.) |
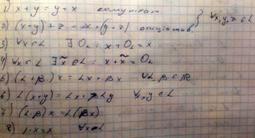





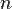 -мірному просторі від базису
-мірному просторі від базису  до базису
до базису  є квадратна матриця, стовпці якої — координати розкладу векторів
є квадратна матриця, стовпці якої — координати розкладу векторів 


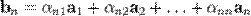

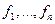 координати ветора у першому базисі.
координати ветора у першому базисі.  координати ветора у другому базисі
координати ветора у другому базисі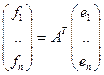 де
де



