
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Означення колінеарності 2-х векторів. Теорема про два колінеарні вектори.Стр 1 из 3Следующая ⇒
Означення колінеарності 2-х векторів. Теорема про два колінеарні вектори.
Два вектори називаються колінеа́рними, якщо вони лежать на паралельних прямих або на одній прямій. Колінеарні вектори можуть бути співнаправленими чи протилежно направленими («антиколінеарними»). Вектори є колінеарними тоді і тільки тоді, коли їхній векторний добуток дорівнює нулю. Два вектори колінеарні, якщо відношення їх координат рівні.
2. Означення компланарності 3-х векторів. Умова компланарності трьох векторів.
Три вектори називаються компланарними, якщо вони лежать на паралельних площинах чи в одній площині. Мішаний добуток компланарних векторів.
Лінійні операції над векторами: означення і властивості.
Лінійними операціями над векторами називаються операції додавання та множення вектора на число (скаляр).
Проекція вектора на вісь. Властивості проекції.
Векторною проекцією вектора Позначають: Проекцією або скалярною проекцією вектора
Властивості проекції вектора на вісь:
Напрямні косинуси вектора. Теорема про геометричний зміст координат вектора. Теорема про геометричний зміст декартових прямокутних координат. Координати вектора в ДПКС дорівнюють проекціям цього вектора на відповідні координатні осі.
6. Скалярним добутком двох векторів
враховуючи, що
то маємо геометричний зміст скалярного добутку:
Властивості скалярного добутку 2-х векторів.
Означення векторного добутку 2-х векторів. Вираз векторного добутку через координати.
Властивості векторного добутку двох векторів.
10.
11. Властивості мішаного добутку.
12.
Означення визначника n-го порядку. Формули обчислення визначників 2-го та 3-го порядку.
Властивості визначників.
Означення колінеарності 2-х векторів. Теорема про два колінеарні вектори.
Два вектори називаються колінеа́рними, якщо вони лежать на паралельних прямих або на одній прямій. Колінеарні вектори можуть бути співнаправленими чи протилежно направленими («антиколінеарними»). Вектори є колінеарними тоді і тільки тоді, коли їхній векторний добуток дорівнює нулю. Два вектори колінеарні, якщо відношення їх координат рівні.
2. Означення компланарності 3-х векторів. Умова компланарності трьох векторів.
Три вектори називаються компланарними, якщо вони лежать на паралельних площинах чи в одній площині. Мішаний добуток компланарних векторів.
|
|||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 643; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.185.147 (0.015 с.) |

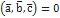


 - задано вектор
- задано вектор U – вісь
U – вісь
 Знайдемо проекції точок А і В на вісь U, для цього через ці точки проведемо площини α та β перпендикулярні до осі U. Таким чином проекціями точок А і В будуть точки А1 та В1.
Знайдемо проекції точок А і В на вісь U, для цього через ці точки проведемо площини α та β перпендикулярні до осі U. Таким чином проекціями точок А і В будуть точки А1 та В1.

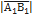 взятий зі знаком +, якщо вектор
взятий зі знаком +, якщо вектор 





 Нехай α, β та γ – це кути, які утворює вектор ā з координатними осями Ox, Oy та Oz відповідно. Тоді cosα, cosβ, cosγ називаються направними косинусами вектора ā. Згідно з попередньою теоремою:
Нехай α, β та γ – це кути, які утворює вектор ā з координатними осями Ox, Oy та Oz відповідно. Тоді cosα, cosβ, cosγ називаються направними косинусами вектора ā. Згідно з попередньою теоремою:
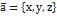






 Означення скалярного добутку 2-х векторів. Вираз скалярного добутку через координати.
Означення скалярного добутку 2-х векторів. Вираз скалярного добутку через координати. і
і  називається число
називається число  , що дорівнює добутку довжин цих векторів на косинус кута між ними. Позначають: (
, що дорівнює добутку довжин цих векторів на косинус кута між ними. Позначають: (








 Означення мішаного добутку 3-х векторів. Вираз мішаного добутку через координати.
Означення мішаного добутку 3-х векторів. Вираз мішаного добутку через координати.


 Означення перестановки, інверсії. Означення визначника n-го порядку.
Означення перестановки, інверсії. Означення визначника n-го порядку.








