
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Управление заемным капиталом предприятияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Задание 5. Рассчитайте ежеквартальную выплату. Предприятие получило кредит в банке на сумму 18000 тыс. руб. под 16% годовых сроком на 3 года. Предполагается выплата кредита аннуитетом с ежеквартальными платежами (1 квартал = 3 месяца).
Формула аннуитетного платежа A = K*S где А - ежемесячный аннуитетный платёж; К - коэффициент аннуитета; S - сумма кредита. Коэффициент аннуитета рассчитывается по следующей формуле:
где i - месячная процентная ставка по кредиту (= годовая ставка / 12); n - количество периодов, в течение которых выплачивается кредит.
Ответ:
Задание 6. Составьте план погашения кредита. Коммерческий банк предоставляет предприятию кредит размером 550 тыс. руб. на 12 месяцев под 15,5% годовых. Долг погашается ежемесячно равными частями, проценты начисляются на остаток долга и выплачиваются ежемесячно.
Ежемесячная сумма погашения основного долга по формуле:
D / (n*m)
где D - величина кредита, m - число погасительных платежей в году, n - срок кредитования в годах.
Общая формула для расчёта процентного платежа применительно к любому месяцу имеет вид:
где Ik - начисленные проценты в k-ом месяце, где k = 1,…,24; i - ставка процентов за кредит, выраженная коэффициентом.
Таблица 16 - План погашения кредита в табличной форме:
Задание 7. Определить подлежащую возврату сумму. Банк выдал кредит 15 января в размере 100 тыс. руб. Срок возврата кредита 15 апреля. Процентная ставка установлена 15% годовых. Год не високосный. Долг гасится единовременным платежом.
Решение: При определении точного количества дней, на которые выдана ссуда, вычитаем 1 день, так как день выдачи и день погашения принимается за один. Можно воспользоваться специальными таблицами порядковых номеров дней в году.
Наращенную сумму долга рассчитаем по формуле:
FV – наращенная сумма денег через определённый период; PV – исходная стоимость денег; t – срок операции; Y – продолжительность года; i – ставка процентов за период.
Ответ:
Движение денежных средств
Задание 8. Составьте план движения денежных средств на планируемый год. Предприятие планирует достичь годового объема реализации продукции в сумме 2 664 тыс. руб. без НДС. Себестоимость реализованной продукции предусматривается в размере 75% от объема реализации. Расходы на сырье и материалы – 50 % от суммы себестоимости реализованной продукции. Оборачиваемость производственных запасов – 8 дн. Денежные средства необходимы предприятию в размере двухнедельной потребности на сырье и материалы. Годовые амортизационные отчисления рассчитаны в сумме 300 тыс. руб. Кредиторская задолженность по товарным операциям составляет величину месячной закупки материальных ресурсов. Прочая кредиторская задолженность – 3 % от объема реализации продукции. В течение года планируется погасить 75 тыс. руб. ранее полученных заемных средств. Инвестиции в основные фонды планируются в размере 520 тыс. руб. Банковский кредит должен составить 50 тыс. руб. Налог на прибыль – 20%. Прибыль к распределению – 256 тыс. руб.
Решение:
План движения денежных средств составляется в виде таблицы установленной формы.
Таблица 17 – План движения денежных средств
Задание 9. Составить план движения денежных средств на год Планом предприятия предусмотрена реализация продукции на 33 120 тыс. руб. Себестоимость реализованной продукции составляет 26 720 тыс. руб., в том числе амортизационные отчисления – 4 010 тыс. руб. В планируемом году предусмотрено приобретение оборудования на сумму 6 820 тыс. руб., планируется привлечь кредит на один год на сумму 850 тыс. руб. под 16% годовых. Налог на прибыль – 20%. Отчисления в резерв – 10% от суммы чистой прибыли. Требуется: 1) составить план движения денежных средств на год; 2) определить остаток денежных средств на конец года, если на начало года он составил 369 тыс. руб.
Задание 10. Определите величину денежных поступлений в июне. Выручка от реализации продукции в январе планируется в размере 600 тыс. руб. В последующие месяцы ожидается ее прирост на 1% ежемесячно. Оплата продукции производится: 20% объема оплачивается наличными; 40% реализуется в кредит с отсрочкой платежа на один месяц; 40% оплачивается через два месяца после отгрузки.
Задание 11. Составьте план движения денежных средств на год и определите их остаток на конец года. Плановый объем выручки от реализации без НДС – 7120 тыс. руб., сумма НДС – 1 424 тыс. руб. Себестоимость реализованной продукции 6 385 тыс. руб., в том числе амортизационные отчисления – 485 тыс. руб. Налоги из прибыли – 580 тыс. руб. Приобретение активов планируется на 860 тыс. руб., а продажа – на 130 тыс. руб. Кредит – 760 тыс. руб. Погашение заемных средств – 120 тыс. руб. Выплата дивидендов – 370 тыс. руб. Остаток денежных средств на начало года не превысит 70 тыс. руб.
Факторный анализ
Задание 12. Изучите методику проведения факторного анализа
Детерминированный факторный анализ имеет достаточно жесткую последовательность выполняемых процедур: - построение экономически обоснованной детерминированной факторной модели; - выбор приема факторного анализа и подготовка условий для его выполнения; - реализация счетных процедур анализа модели; - формулирование выводов и рекомендаций по результатам анализа. Первый этап особенно важен, так как неправильно построенная модель может привести к логически неоправданным результатам. Смысл этого этапа состоит в следующем: любое расширение жестко детерминированной факторной модели не должно противоречить логике связи «причина – следствие». В качестве примера рассмотрим модель, связывающую выручку (В), количество продукции (КП) и цену (Ц). Теоретически можно исследовать три модели: В=КП*Ц; Ц=В/КП; КП=В/Ц Все три формулы верны с позиции арифметики, однако с позиции факторного анализа только первая имеет смысл, поскольку в ней показатели, стоящие в правой части формулы, являются факторами, т. е. причиной, порождающей и определяющей значение показателя, стоящего в левой части (следствие). На втором этапе выбирается один из приемов факторного анализа: интегральный, цепных подстановок, логарифмический и друб. Каждый из этих приемов имеет свои достоинства и недостатки. Краткую сравнительную характеристику этих способов мы рассмотрим ниже.
Существуют следующие модели детерминированного анализа: 1) аддитивная модель, т. е. модель, в которую факторы входят в виде алгебраической суммы, в качестве примера можно привести модель товарного баланса:
где Р - реализация;
П - поступление товаров;
В - прочее выбытие товаров
2) мультипликативная модель, т. е. модель, в которую факторы входят в виде произведения; примером может служить простейшая двухфакторная модель: В=КП*Ц, где В - выручка; КП - количество продукции; Ц – цена. 3) кратная модель, т. е. модель, представляющая собой отношение факторов:
где ОС - стоимость основных средств; Ч – численность 4) смешанная модель, т. е. модель, в которую факторы входят в различных комбинациях, например:
где Р - реализация;
ОС - стоимость основных средств; Об - стоимость оборотных средств. Жестко детерминированная модель, имеющая более двух факторов, называется многофакторной. В детерминированном факторном анализе можно выделить четыре типовые задачи: - оценка влияния относительного изменения факторов на относительное изменение результативного показателя. - оценка влияния абсолютного изменения i-го фактора на абсолютное изменение результативного показателя. - определение отношения величины изменения результативного показателя, вызванного изменением i-го фактора, к базовой величине результативного показателя. - определение доли абсолютного изменения результативного показателя, вызванного изменением i-го фактора, в общем изменении результативного показателя. Охарактеризуем эти задачи и рассмотрим решение каждой из них.
Задание 13. Проведите факторный анализ на основе исходных данных
Объем Выручки (В) зависит от двух основных факторов: количества продукции (КП) и Цены (Ц). Имеем двухфакторную мультипликативную модель: В=КП*Ц. Рассмотрим ситуацию, когда и количество продукции, и цена в отчетном периоде отклонились от запланированных значений.
Таблица 18 - Исходные данные для факторного анализа
Задача имеет смысл для мультипликативных и кратных моделей. Рассмотрим простейшую двухфакторную модель
Очевидно, что при анализе динамики этих показателей будет выполняться следующее соотношение между индексами:
где значение индекса находится отношением значения показателя в отчетном периоде к базисному. Рассчитайте индексы выручки, количества продукции и цены для данного примера:
Согласно вышеприведенному правилу, индекс валовой продукции равен произведению индексов численности работников и среднегодовой выработки, т. е.
Очевидно, что если мы рассчитаем непосредственно индекс валовой продукции, то получим то же самое значение:
Выводы:
Данная задача решается при ответе на вопросы типа: «Что будет, если i-й показатель изменится на n %, а j-й показатель изменится на k %?».
Задание 14. Изучите особенности детерминированного факторного анализа
Общая постановка основной задачей детерминированного факторного анализа имеет следующий вид: Пусть y = f (x1, x2, …, xn) жестко детерминированная модель, характеризующая изменение результативного показателя y от n факторов; все показатели получили приращение
Требуется определить, какой частью приращение результативного показателя y обязано приращению i-го фактора, т. е. расписать следующую зависимость:
где
Основные методы детерминированного факторного анализа
Способ цепной подстановки является весьма простым и наглядным методом, наиболее универсальным из всех. Он используется для расчета влияния факторов во всех типах детерминированных факторных моделей: аддитивных, мультипликативных, кратных и смешанных. Этот способ позволяет определить влияние отдельных факторов на изменение величины результативного показателя путем постепенной замены базисной величины каждого факторного показателя в объеме результативного показателя на фактическую в отчетном периоде. С этой целью определяют ряд условных величин результативного показателя, которые учитывают изменение одного, затем двух, затем трех и т. д. факторов, допуская, что остальные не меняются. Сравнение величины результативного показателя до и после изменения уровня того или иного фактора позволяет определить воздействие конкретного фактора на прирост результативного показателя, исключив влияние остальных факторов. При использовании этого метода достигается полное разложение. При использовании этого способа большое значение имеет очередность изменения значений факторов, так как от этого зависит количественная оценка влияния каждого фактора. Прежде всего, нужно отметить, что не существует и не может существовать единой методики определения этого порядка - существуют модели, в которых он может быть определен произвольно. Лишь для небольшого числа моделей можно использовать формализованные подходы. На практике эта проблема не имеет большого значения, поскольку в ретроспективном анализе важны тенденции и относительная значимость того или иного фактора, а не точные оценки их влияния. Тем не менее, для соблюдения более или менее единого подхода к определению порядка замены факторов в модели можно сформулировать общие принципы. Введем некоторые определения. Признак, непосредственно относящийся к изучаемому явлению и характеризующий его количественную сторону, называется первичным или количественным. Эти признаки: а) абсолютные (объемные); б) их можно суммировать в пространстве и времени. В качестве примера можно привести объем реализации, численность, стоимость оборотных средств и т. д. Признаки, относящиеся к изучаемому явлению не непосредственно, а через один или несколько других признаков и характеризующие качественную сторону изучаемого явления, называются вторичными или качественными. Эти признаки: а) относительные; б) их нельзя суммировать в пространстве и времени. Примерами могут служить фондовооруженность, рентабельность и др. В анализе выделяют вторичные факторы 1-го, 2-го и т. д. порядков, получаемые путем последовательной детализации. Жестко детерминированная факторная модель называется полной, если результативный показатель количественный, и неполной, если результативный показатель качественный. В полной двухфакторной модели один фактор всегда количественный, второй - качественный. В этом случае замену факторов рекомендуют начинать с количественного показателя. Если же имеется несколько количественных и несколько качественных показателей, то сначала следует изменить величину факторов первого уровня подчинения, а потом более низкого. Таким образом, применение способа цепной подстановки требует знания взаимосвязи факторов, их соподчиненности, умения правильно их классифицировать и систематизировать.
Теперь рассмотрим на нашем примере порядок применения способа цепных подстановок. Алгоритм расчета способом цепной подстановки для данной модели выглядит следующим образом:
Выводы:
Таким образом, перевыполнение плана по объему выручки явилось результатом влияния следующих факторов:
Алгебраическая сумма факторов при использовании данного метода обязательно должна быть равна общему приросту результативного показателя:
Отсутствие такого равенства свидетельствует о допущенных ошибках в расчетах. Другие методы анализа, такие как интегральный и логарифмический, позволяют достичь более высокой точности расчетов, однако эти методы имеют более ограниченную сферу применения и требуют проведения большого объема вычислений, что неудобно для проведения оперативного анализа. Задание 15. Данное задание является в определенном смысле следствием второй типовой задачи, поскольку базируется на полученном факторном разложении. Необходимость решения этой задачи обусловлена тем обстоятельством, что элементы факторного разложения составляют абсолютные величины, которые трудно использовать для пространственно-временных сопоставлений. При решении задачи 3 факторное разложение дополняется относительными показателями:
Экономическая интерпретация: коэффициент Рассчитаем коэффициенты α для нашего примера, используя факторное разложение, полученное ранее методом цепных подстановок:
Выводы:
Задание 16. Данное задание также решается на основе базовой задачи 2 и сводится к расчету показателей:
Экономическая интерпретация: коэффициент показывает долю прироста результативного показателя, обусловленную изменением i-го фактора. Здесь не возникает вопроса, если все факторные признаки изменяются однонаправленно (либо возрастают, либо убывают). Если это условие не выполняется, решение задачи может быть осложнено. В частности, в наиболее простой двухфакторной модели в подобном случае расчет по приведенной формуле не выполняется и считается, что 100% прироста результативного показателя обусловлены изменением доминирующего факторного признака, т. е. признака, изменяющегося однонаправленно с результативным показателем. Рассчитаем коэффициенты γ для нашего примера, используя факторное разложение, полученное методом цепных подстановок:
Выводы:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 520; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.255.103 (0.011 с.) |


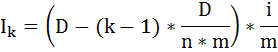

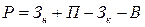 ,
,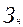 - запасы на начало периода;
- запасы на начало периода; - запасы на конец периода;
- запасы на конец периода; ,
, - фондовооруженность;
- фондовооруженность; ,
, - рентабельность;
- рентабельность;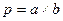 .
. ,
,

 =
=
 (например, в динамике, по сравнению с планом, по сравнению с эталоном):
(например, в динамике, по сравнению с планом, по сравнению с эталоном):


 ,
, - общее изменение результативного показателя, складывающееся под одновременным влиянием всех факторных признаков;
- общее изменение результативного показателя, складывающееся под одновременным влиянием всех факторных признаков; - изменение результативного показателя под влиянием только фактора
- изменение результативного показателя под влиянием только фактора  .
.



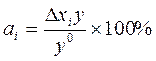
 показывает, на сколько процентов к базисному уровню изменился результативный показатель под влиянием i-го фактора.
показывает, на сколько процентов к базисному уровню изменился результативный показатель под влиянием i-го фактора.
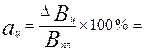
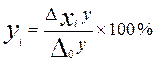
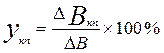 =
=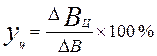 =
=


