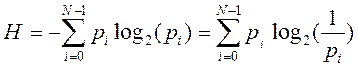Содержательный подход к измерению информации

Теория

Согласно Шеннону, информативность сообщения характеризуется содержащейся в нем полезной информацией — той частью сообщения, которая снимает полностью или уменьшает неопределенность какой-либо ситуации.

Неопределенность некоторого события — это количество возможных исходов данного события.

Пусть в некотором сообщении содержатся сведения о том, что произошло одно из N равновероятных (равновозможных) событий. Тогда количество информации i, заключенное в этом сообщении, и число событий N связаны формулой: 2ⁱ = N (или i=log₂N). Эта формула носит название формулы Хартли.

В общем случае, если N – количество возможных событий, p_i – вероятности отдельных событий, применяется формула Шеннона:

 

 

Энтропия (H) – мера неопределенности, выраженная в битах.

Количество информации I и энтропия H характеризуют одну и ту же ситуацию, но с качественно противоположенных сторон.

I – это количество информации, которое требуется для снятия неопределенности H.

Когда неопределенность снята полностью, количество полученной информации I равно изначально существовавшей неопределенности H.

 

Примеры

1. Сколько бит информации несет сообщение о том, что из 256 одинаковых по размеру, но разноцветных шаров наугад выбрали красный шар?

Решение: Выбор шара любого цвета, в том числе и красного – события равновероятностные, следовательно, i = log₂256 = 8(бит).

Ответ: сообщение о том, что из 256 одинаковых по размеру, но разноцветных шаров наугад выбрали красный шар, несет 8бит.

2. В гимназический класс школы были отобраны ученики из 128 претендентов. Какое количество учеников было отобрано, если сообщение о том, кто был отобран, содержит 140 битов информации?

Решение: Определим, сколько бит содержит сообщение об одном ученике. 2ⁱ = N, 2ⁱ = 128, i = 7(бит). Т.о. было отобрано 140 / 7 = 20 человек.

Ответ: 20 человек было отобрано в гимназический класс.

3. В озере живут караси и окуни. Вероятность попадания на удочку карася – 0,75; окуня – 0,25. Сколько информации содержится в сообщении, что рыбак поймал рыбу?

Решение: По формуле Шеннона

 

 

Ответ: в сообщении, что рыбак поймал рыбу содержится 0,8 бит информации.

Задачи для самостоятельного решения

1. В барабане для розыгрыша лотереи находится 32 шара. Сколько информации содержится в сообщении о первом выпавшем номере (например, выпал номер 15)?

2. При угадывании целого числа в диапазоне от 1 до N было получено 6 бит информации. Чему равно N?

3. Сообщение о том, что из корзины с разноцветными шарами (все шары разного цвета) достали зеленый шар, содержит 4 бита информации. Сколько шаров было в корзине?

4. Из папки NEW одновременно удалили 10 файлов. Сообщение о названиях удаленных файлов содержит 80 бит информации. Сколько файлов было всего в папке?

5. В доме 4 подъезда, в каждом из которых 16 этажей. Какое количество информации содержится в сообщении о том, что Иван живет на пятом этаже в третьем подъезде?

6. Система может находиться в трех различных состояниях с вероятностями: в первом (худшем) состоянии с вероятностью 0,1; во втором – 0,4; в третьем (лучшем) – 0,5. Чему равно количество информации о произвольном состоянии системы?