Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дробно-линейное программирование. Математическая модель задачи. Использование дробно-линейного программирования в управлении.Содержание книги
Поиск на нашем сайте
Дробно-линейное программирование относится к нелинейному программированию, так как имеет целевую функцию, заданную в нелинейном виде. Задача дробно-линейного программирования в общем виде записывается следующим образом:
При ограничениях:
где сj, dj, bi, aij - постоянные коэффициенты и Рассмотрим задачу дробно-линейного программирования в виде:
При ограничениях:
Будем считать, что Для решения этой задачи найдем область допустимых решений, определяемую ограничениями (8-9). Пусть эта область не является пустым множеством. Из выражения (7) найдем x2:
где Прямая x2 = kx1 проходит через начало координат. При некотором фиксированном значении L угловой коэффициент k прямой тоже фиксирован и прямая займет определенное положение. При изменении значений L прямая x2 = kx1 будет поворачиваться вокруг начала координат (рис. 28.6).
Установим, как будет вести себя угловой коэффициент k при монотонном возрастании L. Найдем производную от k по L:
Знаменатель производной всегда положителен, а числитель от L не зависит. Следовательно, производная имеет постоянный знак и при увеличении L угловой коэффициент будет только возрастать или только убывать, а прямая будет поворачиваться в одну сторону. Если угловой коэффициент прямой имеет положительное значение, то прямая вращается против часовой стрелки, при о трицательном значении k - по часовой стрелке. Установив направление вращения, находим вершину или вершины многогранника, в которых функция принимает max(min) значение, либо устанавливаем неограниченность задачи. При этом возможны следующие случаи: 1. ОДР ограничена, максимум и минимум достигаются в ее угловых точках (рис. 28.7). 2. ОДР неограничена, однако существуют угловые точки, в которых целевая функция принимает максимальное и минимальное значения (рис. 28.8). 3. ОДР неограничена, имеется один из экстремумов. Например, минимум достигается в одной из вершин области и имеет так называемый асимптотический максимум (рис. 28.9). 4. ОДР неограничена. Максимум и минимум являются асимптотическими (рис. 28.10).
Таким образом, алгоритм решения задач дробно-линейного программирования следующий: 1. Находим область допустимых решений (ОДР). 2. Определяем угловой коэффициент k и устанавливаем направление поворота целевой функции. 3. Находим точку max(min) целевой функции или устанавливаем неразрешимость задачи. Экономическая интерпретация задач дробно-линейного программирования Математическая модель задачи дробно-линейного программирования может быть использована, например, для определения рентабельности затрат на производство изделий, рентабельности продаж, затрат в расчете на гривну выпускаемой продукции, себестоимости изделий. Обозначим: Rj - прибыль предприятия от реализации единицы изделия j-гo вида; Xj - количество выпущенной продукции j-гo вида; Sj - цена единицы продукции j-гo вида; Cj - себестоимость производства единицы изделия j-гo вида; Dj - затраты на производство одного изделия j-гo вида. Задача рентабельности (РЗ) затрат на производство изделий имеет вид:
Задача рентабельности (Рп) продаж имеет вид:
Задача определения затрат (Згрн) в расчете на гривну товарной продукции записывается в виде:
Задача нахождения себестоимости изделия записывается как:
Указанные математические модели имеют системы ограничений в зависимости от условий задачи. Применение дробно-линейного программирования для определения себестоимости изделий Задача №3. Для производства двух видов изделий А и В предприятие использует три типа технологического оборудования. Каждое из изделий должно пройти обработку на каждом из типов оборудования. Время обработки каждого из изделий, затраты, связанные с производством одного изделия, даны в таблице:
Оборудование I и III типов предприятие может использовать не более 26 и 39 часов соответственно, оборудование II типа целесообразно использовать не менее 4 часов. Определить, сколько изделий каждого вида следует изготовить предприятию, чтобы средняя себестоимость одного изделия была минимальной. Решение. Составим математическую модель задачи. Пусть X1 - количество изделий вида А, которое следует изготовить предприятию, X2 — количество изделий вида В. Общие затраты на их производство составят (2Х1 + 3X2) тыс. грн., а средняя себестоимость одного изделия будет равна:
Математическая модель задачи примет вид:
при ограничениях:
ΔАВС — область допустимых решений (рис. 28.11).
Найдем X2:
Угловой коэффициент прямой равен k = (L - 2)/(3- L), тогда:
Так как Найдем координаты точки С. Решая систему:
X1=3, X2=1, получим С (3, 1), Х* = (3, 1), L = 9/4. Следовательно, предприятию следует выпускать 3 изделия вида А и 1 изделие вида В. При этом средняя себестоимость одного изделия будет минимальной и равной 2,25 тыс. грн.
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 597; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.92.96 (0.006 с.) |

 (4)
(4)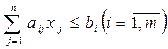 (5)
(5) (6)
(6)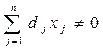 .
. (7)
(7) (8)
(8)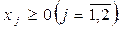 (9)
(9) .
.


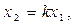
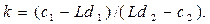



 (10)
(10) (11)
(11) (12)
(12) (13)
(13) .
.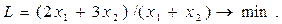

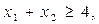

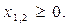






 , то функция k =(L-2)/(3-L) возрастает. Это соответствует вращению прямой против часовой стрелки. Следовательно, в точке С (рис. 28.11) целевая функция будет иметь наименьшее значение (глобальный минимум).
, то функция k =(L-2)/(3-L) возрастает. Это соответствует вращению прямой против часовой стрелки. Следовательно, в точке С (рис. 28.11) целевая функция будет иметь наименьшее значение (глобальный минимум).