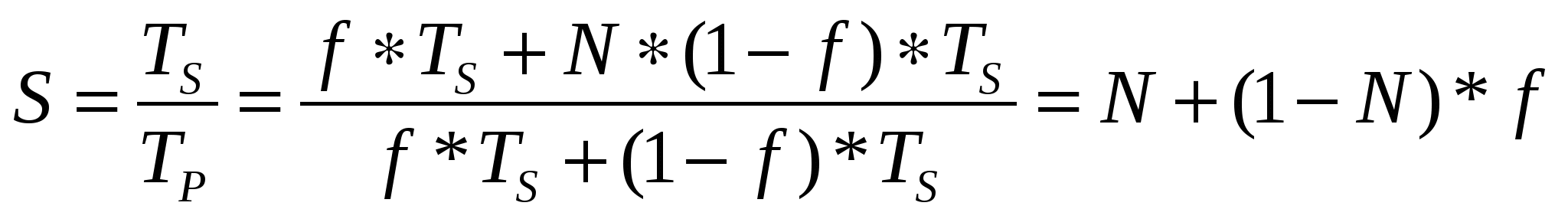Закон Густафсона для масштабируемых задач

Одним из недостатков закона Амдала в плане его применимости состоит в том, что он не дает ответа в случае, когда при увеличении размера вычислительной системы и связанного с этим ростом вычислительной мощности, увеличивают и размер решаемой задачи. Наличие широкого круга приложений, критичных к времени вычислений, стало одним из побудительных мотивов для совершенствования концепции ускорения при фиксированной нагрузке и согласованного с ней закона Амдала. По мере того, как мы увеличиваем размер вычислительной системы, чтобы повысить ее мощность, возникает желание увеличить размер решаемой задачи, с тем, чтобы увеличить рабочую нагрузку, сохраняя неизменным время вычислений.

Известную долю оптимизма в оценку, даваемую законом Амдала, вносят исследования Джона Густафсона из NASA Ames research. Решая на вычислительной системе из 1024 процессоров три больших задачи, для которых доля последовательного кода f лежала в пределах 0.4-0.8 % он получил ускорения по сравнению с однопроцессорным вариантом, равные соответственно 1021, 1020 и 1016. Согласно закону Амдала для данного числа процессоров и диапазона f, ускорение не должно было превысить величину порядка 201. Пытаясь объяснить это явление, Густафсон пришел к выводу, что причина кроется в исходной предпосылке, лежащей в основе закона Амдала: увеличение числа процессоров не сопровождается увеличением объема решаемой задачи. Реальное же поведение пользователей существенно отличается от такого представления. Обычно получая в свое распоряжение более мощную систему, пользователь не стремится сократить объем вычислений, а сохраняя его практически неизменным, старается пропорционально приросту вычислительной мощности ВС увеличить объем решаемой задачи. И тут оказывается, что наращивание общего объема программы касается главным образом распараллеливаемой части программы. Это ведет к сокращению значения f. Примером может служить решение дифференциального уравнения в частных производных. Если доля последовательного кода составляет 10% для 1000 узловых точек, то для 100000 точек доля последовательного кода снизится до 0.1%. Сказанное иллюстрирует рис. 10.4, который отражает тот факт, что оставаясь практически неизменной, последовательная часть кода в общем объеме увеличенной программы имеет уже меньший удельный вес.

Было отмечено, что в первом приближении объем работы, которая может быть произведена параллельно, возрастает линейно с ростом числа процессоров в системе. Для того чтобы оценить возможность ускорения вычислений, когда объем последних увеличивается с ростом количества процессоров в системе (при постоянстве общего времени вычислений), Густафсон рекомендует использовать выражение, предложенное Е. Барсисом (E. Barsis):

Из выражения следует, что если объем задачи возрастает одновременно с мощностью системы, последовательная часть перестает быть узким местом.

Данное выражение известно как закон масштабируемого ускорения или закон Густафсона-Барсиса. Отметим, что этот закон не противоречит закону Амдала. Различие состоит лишь в форме утилизации дополнительной вычислительной мощности, возникающей при увеличении числа процессоров.