
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон Амдала и его следствияСодержание книги Поиск на нашем сайте Приобретая для решения своей задачи параллельную вычислительную систему, пользователь рассчитывает на значительное повышение скорости вычислений за счет распределения вычислительной нагрузки по множеству параллельно работающих процессоров. В идеальном случае система из N процессоров могла бы ускорить вычисления в N раз. В реальности достичь такого показателя по ряду причин не удается. Главная из этих причин заключается в невозможности полного распараллеливания ни одной из задач. Как правило, в каждой программе имеется фрагмент кода, который принципиально должен выполняться последовательно и только одним из процессоров. Это может быть часть программы, отвечающая за запуск задачи и распределение распараллеленного кода по процессорам, либо фрагмент программы, обеспечивающий операции ввода/вывода. Можно привести и другие примеры, но главное состоит в том, что о полном распараллеливании задачи говорить не приходится. Известные проблемы возникают и с той частью задачи, которая поддается распараллеливанию. Здесь идеальным был бы вариант, когда параллельные ветви программы постоянно загружали бы все процессоры системы, причем так, чтобы нагрузка на каждый процессор была одинакова. К сожалению, оба этих условия на практике трудно реализуемы. Таким образом, ориентируясь на параллельную ВС, необходимо четко сознавать, что добиться прямо пропорционального числу процессоров увеличения производительности не удастся, и, естественно, встает вопрос о том, на какое реальное ускорение можно рассчитывать. Ответ на этот вопрос в какой-то мере дает закон Амдала. Джин Амдал (Gene Amdahl) — один из разработчиков всемирно известной системы IBM 360, в своей работе [48], опубликованной в 1967 году, предложил формулу, отражающую зависимость ускорения вычислений, достигаемого на многопроцессорной ВС, от числа процессоров и соотношения между последовательной и параллельной частями программы. Показателем сокращения времени вычислений служит такая метрика, как «ускорение». Напомним, что ускорение S — это отношение времени
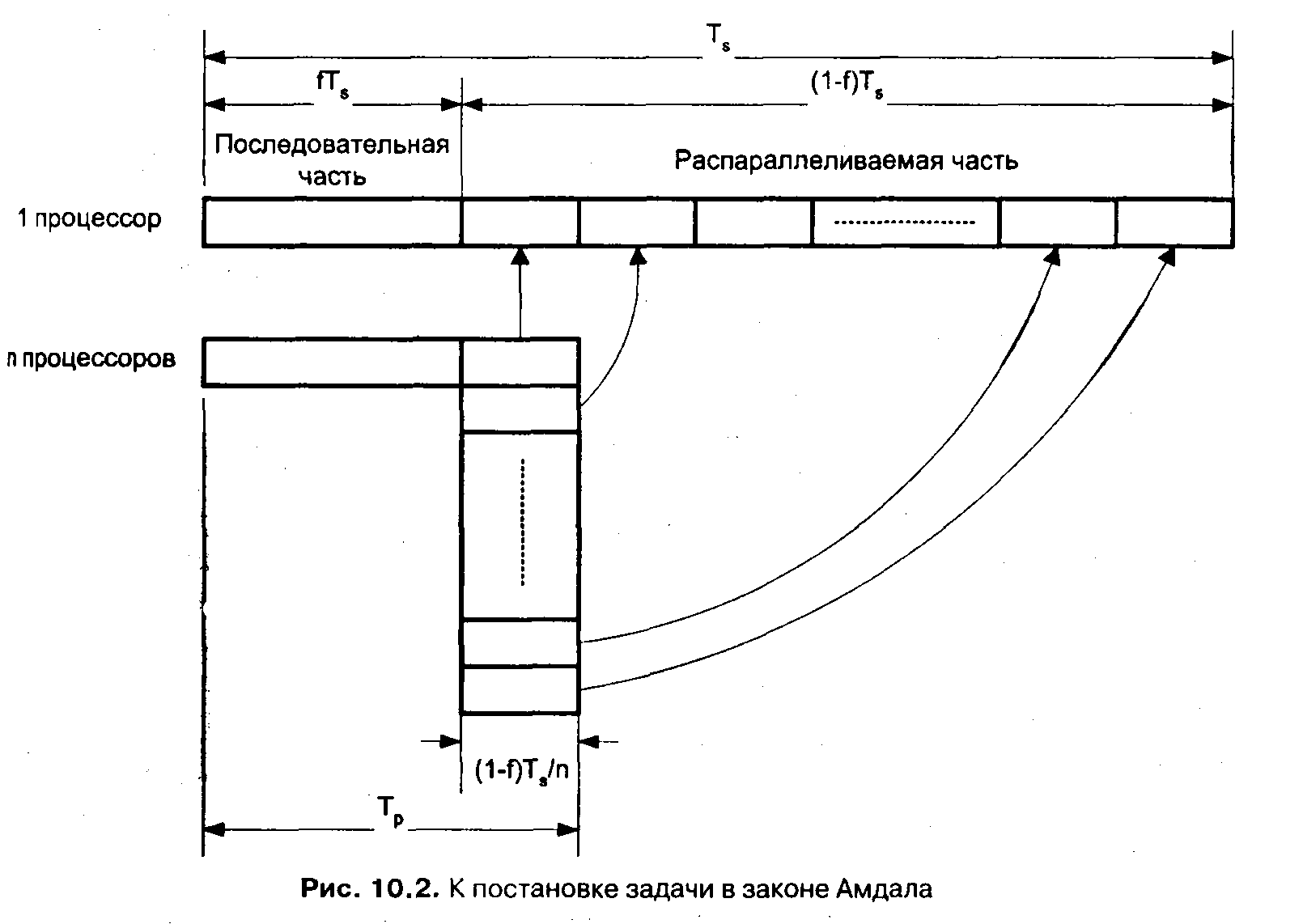
Оговорки относительно алгоритмов решения задачи сделаны, чтобы подчеркнуть тот факт, что для последовательного и параллельного решения лучшими могут оказаться разные реализации, а при оценке ускорения необходимо исходить именно из наилучших алгоритмов. Проблема рассматривалась Амдалом в следующей постановке (рис. 10.2).
Прежде всего, объем решаемой задачи с изменением числа процессоров, участвующих в ее решении, остается неизменным. Программный код решаемой задачи состоит из двух частей: последовательной и распараллеливаемой. Обозначим долю операций, которые должны выполняться последовательно одним из процессоров, через f, где 0 ≤ f ≤ 1 (здесь доля понимается не по числу строк кода, а по числу реально выполняемых операций). Отсюда доля, приходящаяся на распараллеливаемую часть программы, составит (1–f). Крайние случаи в значениях f соответствуют полностью параллельным (f=0) и полностью последовательным (f= 1) программам. Распараллеливаемая часть программы равномерно распределяется по всем процессорам. С учетом приведенной формулировки имеем:
В результате получаем формулу Амдала, выражающую ускорение, которое может быть достигнуто на системе из N процессоров:
Закон Амдала констатирует, что максимальное ускорение для алгоритма ограничено относительным числом операций, которые должны быть выполнены последовательно, то есть последовательной частью алгоритма. Отметим, что при
Рис. 6. Зависимость ускорения от величины a для двух систем: с 10 процессорами и с 1024 процессорами
Рис. 7. Зависимость ускорения от числа процессоров для различных значений a Следствия из закона Амдала:
Отсюда первый вывод - прежде, чем основательно переделывать код для перехода на параллельный компьютер (а любой суперкомпьютер, в частности, является таковым) надо основательно подумать. Если, оценив заложенный в программе алгоритм, вы поняли, что доля последовательных операций велика, то на значительное ускорение рассчитывать явно не приходится и нужно думать о замене отдельных компонентов алгоритма. В ряде случаев последовательный характер алгоритма изменить не так сложно. Допустим, что в программе есть следующий фрагмент для вычисления суммы n чисел: s:= 0 Do i = 1, n s = s + a(i) EndDo По своей природе он строго последователен, так как на i-й итерации цикла требуется результат с (i-1)-й и все итерации выполняются одна за одной. Имеем 100% последовательных операций, а значит и никакого эффекта от использования параллельных компьютеров. Вместе с тем, выход очевиден. Поскольку в большинстве реальных программ1 нет существенной разницы, в каком порядке складывать числа, выберем иную схему сложения. Сначала найдем сумму пар соседних элементов: a(1)+a(2), a(3)+a(4), a(5)+a(6) и т.д. Заметим, что при такой схеме все пары можно складывать одновременно! На следующих шагах будем действовать абсолютно аналогично, получив вариант параллельного алгоритма. Казалось бы в данном случае все проблемы удалось разрешить. Но представьте, что доступные вам процессоры разнородны по своей производительности. Значит, будет такой момент, когда кто-то из них еще трудится, а кто-то уже все сделал и бесполезно простаивает в ожидании. Если разброс в производительности компьютеров большой, то и эффективность всей системы при равномерной загрузке процессоров будет крайне низкой. Но пойдем дальше и предположим, что все процессоры одинаковы. Проблемы кончились? Опять нет! Процессоры выполнили свою работу, но результат-то надо передать другому для продолжения процесса суммирования... а на передачу уходит время... и в это время процессоры опять простаивают... Словом, заставить параллельную вычислительную систему или супер-ЭВМ работать с максимальной эффективность на конкретной программе это, прямо скажем, задача не из простых, поскольку необходимо тщательное согласование структуры программ и алгоритмов с особенностями архитектуры параллельных вычислительных систем.
|
||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 822; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

 , затрачиваемого на проведение вычислений на однопроцессорной ВС (в варианте наилучшего последовательного алгоритма), ко времени
, затрачиваемого на проведение вычислений на однопроцессорной ВС (в варианте наилучшего последовательного алгоритма), ко времени  решения той же задачи на параллельной системе (при использовании наилучшего параллельного алгоритма):
решения той же задачи на параллельной системе (при использовании наилучшего параллельного алгоритма):
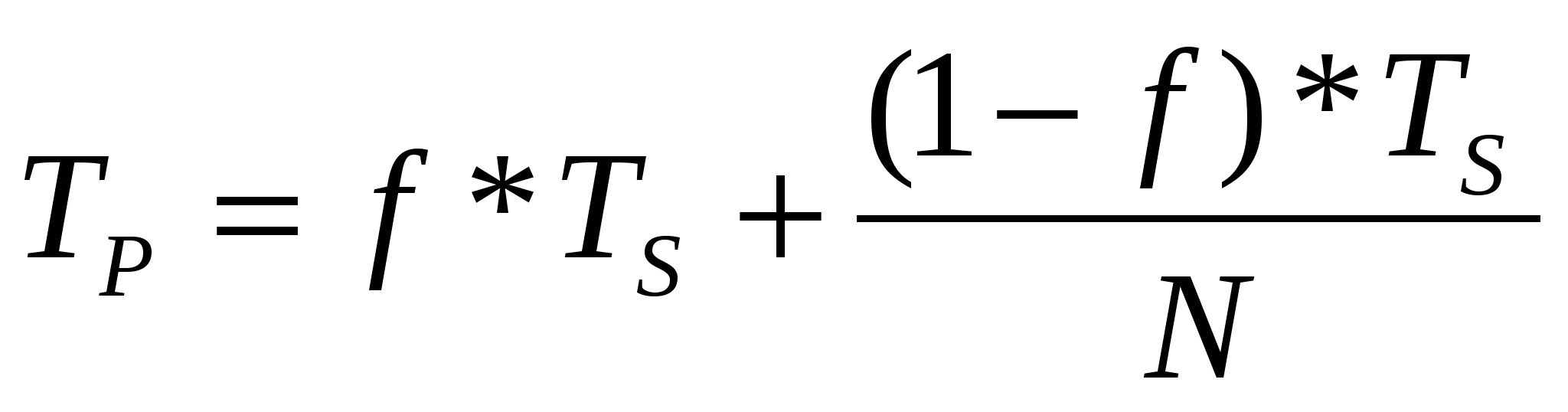

 величина ускорения
величина ускорения  , то есть ускорение всегда ограничено величиной
, то есть ускорение всегда ограничено величиной  , независимо от числа используемых процессоров. Проявление закона Амдала при N = 10 и N = 1024 показано на рис. 6. Если параллельная программа содержит 1% последовательного кода, то максимальное ускорение на 10 процессорах будет равно 9, а на 1024 процессорах — только 91. На рис. 7 приведена зависимость ускорения от числа процессоров для различных значений f.
, независимо от числа используемых процессоров. Проявление закона Амдала при N = 10 и N = 1024 показано на рис. 6. Если параллельная программа содержит 1% последовательного кода, то максимальное ускорение на 10 процессорах будет равно 9, а на 1024 процессорах — только 91. На рис. 7 приведена зависимость ускорения от числа процессоров для различных значений f.




