Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модель ускорения при фиксированном размере памятиСодержание книги Поиск на нашем сайте
Пусть M — это требования к емкости памяти, необходимой для решения определенной проблемы, а W — вычислительная нагрузка. Эти два фактора влияют друг на друга по-разному, в зависимости от адресного пространства и архитектурных ограничений. Запишем это в виде W = g(M) или M = g-1(W). В многопроцессорной системе емкость памяти растет линейно с увеличением числа узлов. Запишем рабочую нагрузку последовательного выполнения вычислений на одном узле, как Ускорение при фиксированной памяти определяется аналогично тому, как это рассматривалось раньше:
Ранее уже отмечалось, что с увеличением числа узлов системы пропорционально увеличивается и емкость памяти. Для гомогенной системы из n узлов полагаем, что g*(nM) = G(n)g(M) = G(n). Здесь коэффициент G(n) отражает рост рабочей нагрузки с увеличением памяти в n раз. В предположении о том, что Wi = 0, если i ¹ 1 или i ¹ n и Q(n) = 0, последнее выражение для ускорения можно записать в виде:
Модель фиксированной памяти также предполагает масштабируемую рабочую нагрузку и допускает небольшое увеличение времени вычислений. Увеличение рабочей нагрузки (размера задачи) ограничено размером памяти. Рост размера системы при большом числе процессоров ограничен увеличением времени на обмен информацией между процессорами. Проиллюстрируем эту концепцию для алгоритма перемножения матриц. Полагаем, что алгоритм содержит фиксированную последовательную часть и полностью распараллеливаемую остальную часть. Положим также, что для одного процессора размерность матрицы равна m. Время последовательного исполнения равно T(1) = W1 + Wn = W1 + m3 T*(1)=W1+n3/2m3 Но с n процессорами мы получаем T*(1)=W1+n1/2m3 Таким образом, ускорение равно
Для матричного умножения время вычисления возрастает быстрее, чем требования к памяти. Следовательно, чем мощнее ВС, тем большая проблема может быть решена, но время выполнения растет, даже если система становится все быстрее и быстрее. В терминах ускорения это дает даже более оптимистичную картину по сравнению с ускорением при фиксированном времени.
|
||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 345; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

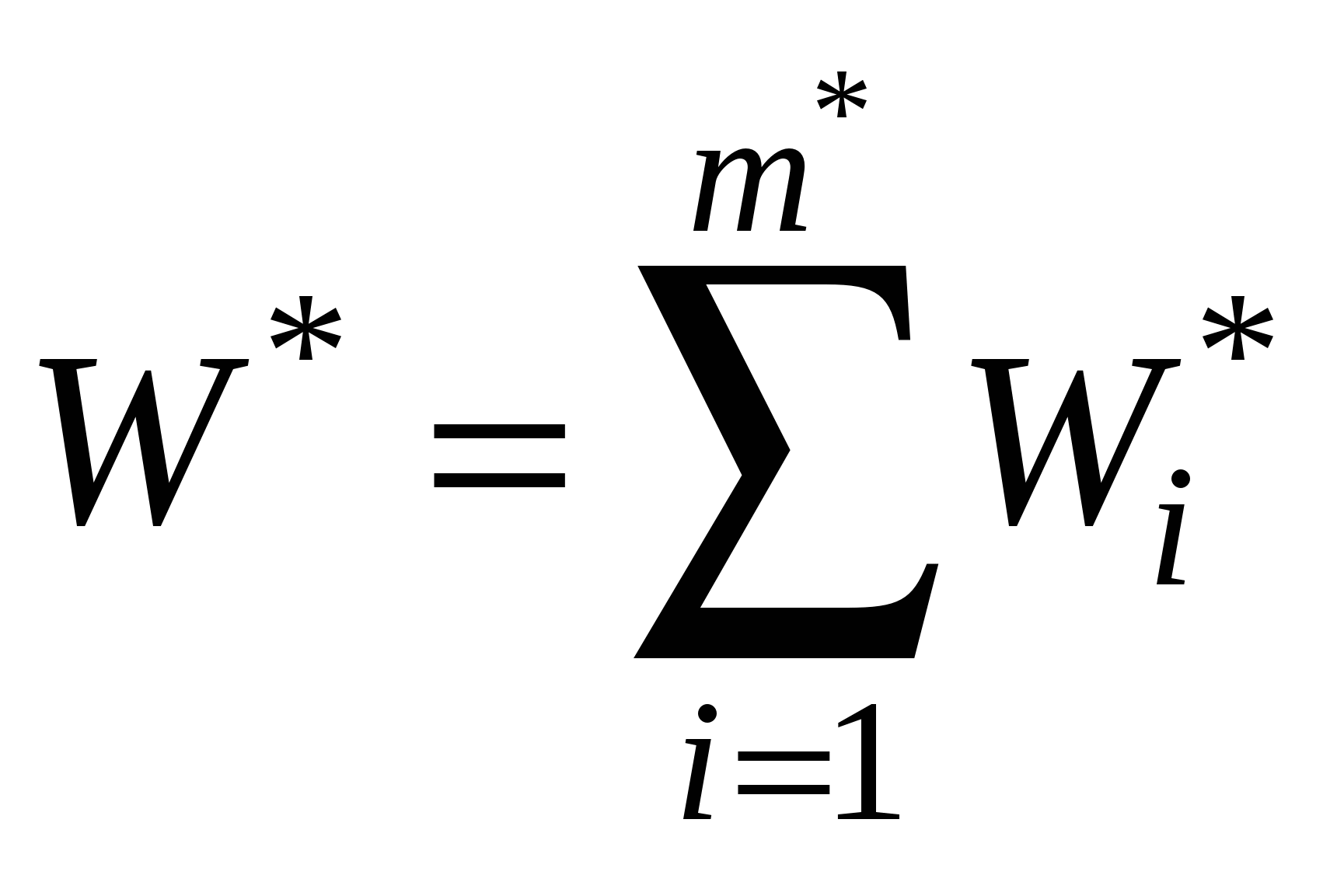 , а масштабированную рабочую нагрузку для выполнения на n узлах —
, а масштабированную рабочую нагрузку для выполнения на n узлах — 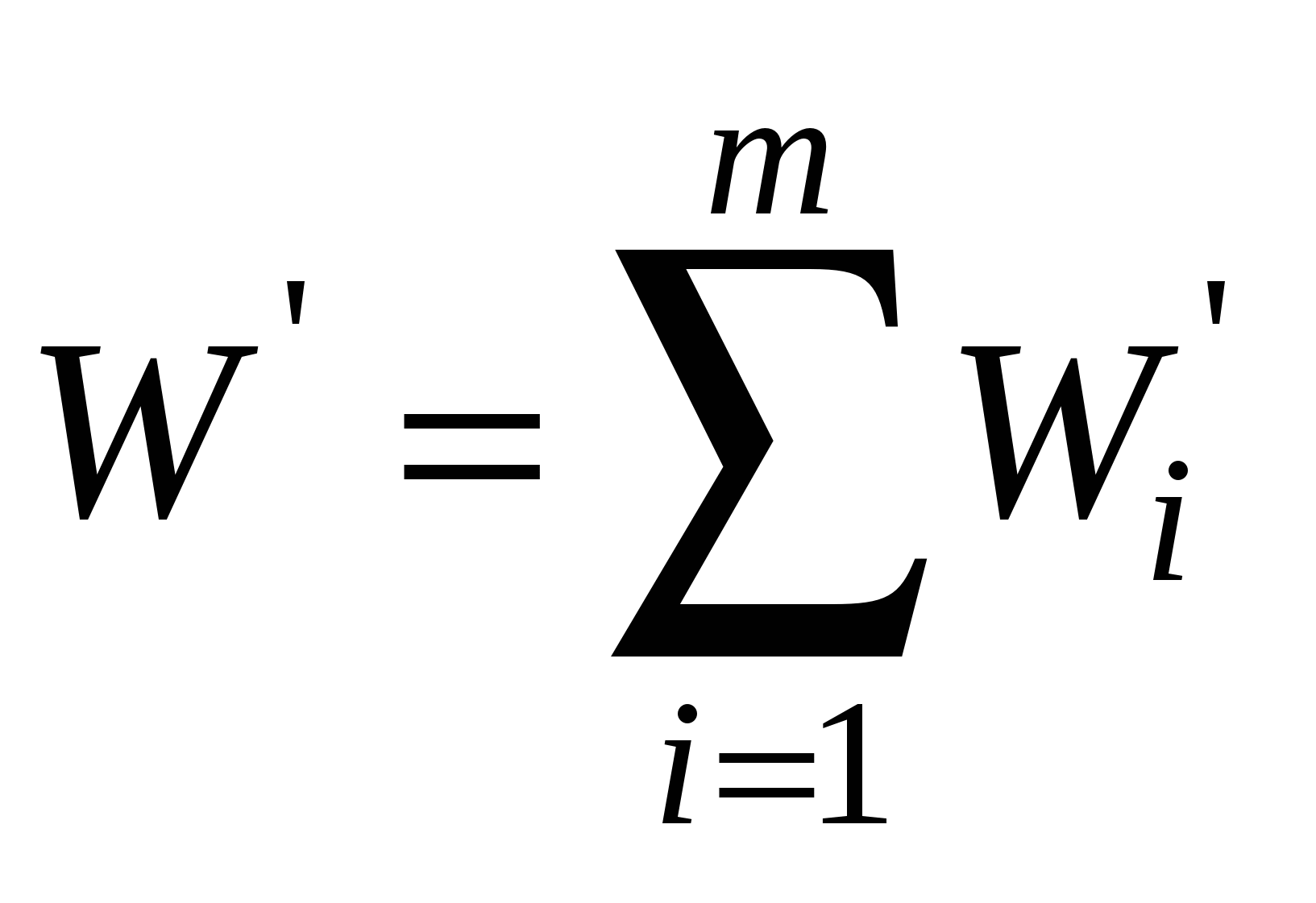 , где m* — максимальная степень параллелизма в масштабированной (увеличенной) задаче. Тогда требования к емкости памяти для активного узла можно записать в виде
, где m* — максимальная степень параллелизма в масштабированной (увеличенной) задаче. Тогда требования к емкости памяти для активного узла можно записать в виде  .
.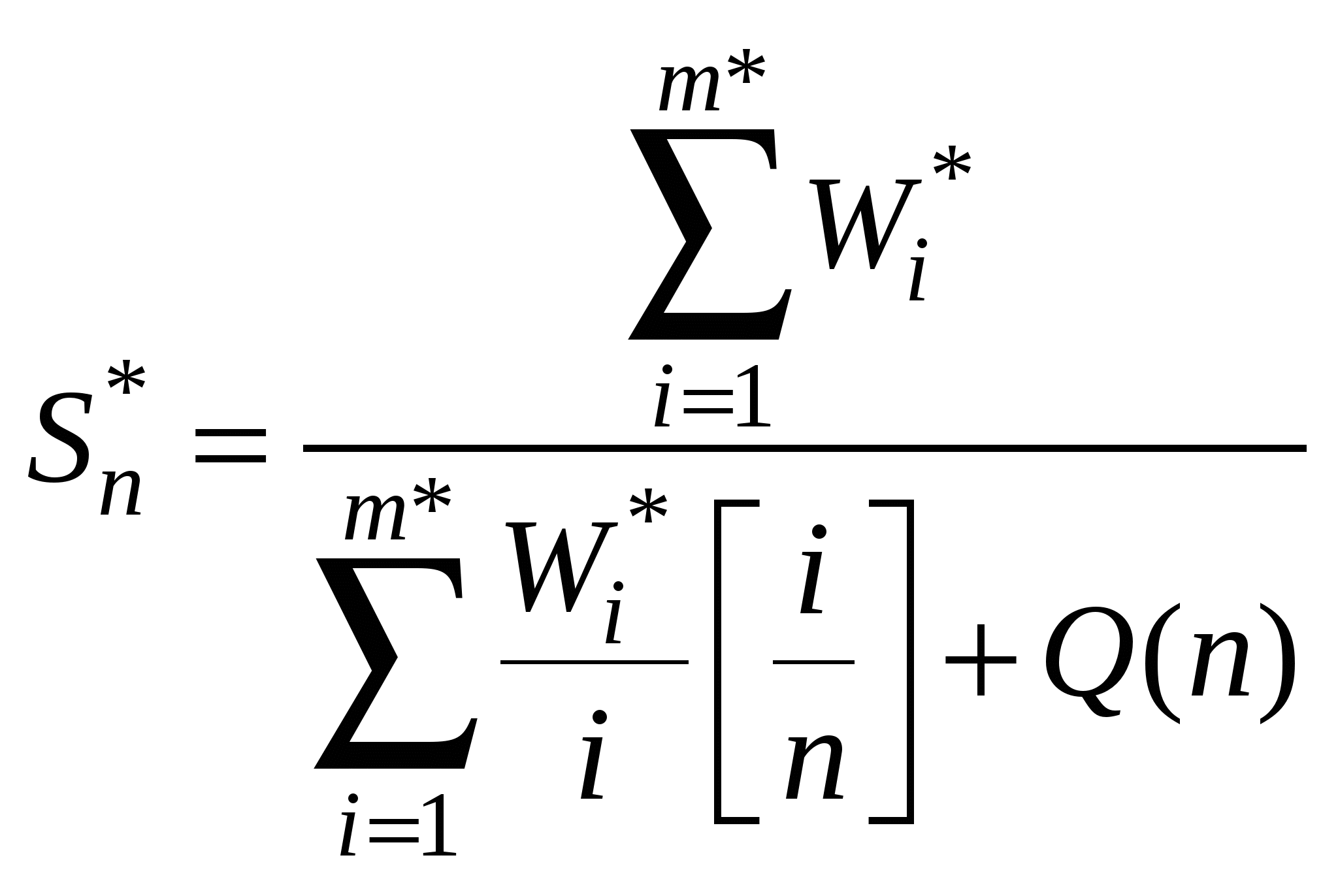
 .
. поэтому гипотетическое время последовательного исполнения будет
поэтому гипотетическое время последовательного исполнения будет