
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Невозможен процесс, единственным результатом которого является передача энергии в форме теплоты от холодного тела к горячему.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
А также: В изолированной системе самопроизвольные процессы происходят в направлении увеличения энтропии: DS ³ 0. Энтропия (S) – это функция состояния, являющаяся количественной мерой неупорядоченности в системе. В наиболее неупорядоченном состоянии энтропия будет максимальной. Единицы измерения энтропии: Дж/моль×К. Больцманом было предложено уравнение, в котором энтропия выражена через термодинамическую вероятность (W): S = k×lnW, где k – константа Больцмана, равная 1.38×10 –23 Дж/К. III закон термодинамики Энтропия идеального ионного кристалла при температуре абсолютного нуля (0 К) равна нулю. Таким образом, устойчивость любой системы определяется соотношением энтальпийного и энтропийного параметров, поэтому целесообразно было ввести такую функцию состояния, которая бы учитывала совместное влияние обоих факторов. Эта функция состояния называется энергией Гиббса: DG = DH – TDS. По знаку функции энергии Гиббса судят о возможности самопроизвольного протекания процесса: Ø если DG < 0, то процесс термодинамически разрешен, Ø если DG > 0, то самопроизвольный процесс невозможен (запрещен по термодинамике), Ø если DG = 0, то система находится в состоянии равновесия. Изменение энергии Гиббса для реакции также можно рассчитать, если известны стандартные энергии Гиббса образования веществ: D r G0 = Si×D f G0продуктов – Si×D f G0реагентов. Обучающие задачи Задача 1. Почему термодинамические параметры называют параметрами состояния? Можно ли с этой точки зрения объяснить, почему на основании закона Гесса можно рассчитывать изменения не только энтальпии, но также и энтропии, энергии Гиббса? Ответ. Изменение величин термодинамических параметров, характеризующих систему, не зависит от путей перехода системы из одного состояния в другое, поэтому термодинамические параметры называют параметрами состояния. К ним относятся Н, S, G, F и др. Так как закон Гесса справедлив для параметров состояния, то следствия закона Гесса используют для расчета DН, DS, DG и других функций состояния. Задача 2. Используя формулировку I закона термодинамики, объясните, существует ли вечный двигатель I рода, который мог бы производить больше энергии, чем потреблять в процессе своей работы?
Ответ. Согласно I закону термодинамики энергия изолированной системы не может возрастать в результате протекающих в ней процессов. Следовательно, нельзя сконструировать устройство для получения энергии из ничего, т. е. вечный двигатель невозможен. Российская Академия наук в XVIII веке прекратила рассматривать все заявки, претендующие на изобретение вечного двигателя. Задача 3. Согласно II закону термодинамики в изолированных системах все самопроизвольно протекающие процессы идут с увеличением энтропии. Протекание же самого масштабного на нашей планете процесса фотосинтеза согласно уравнению реакции 6CO2 + 6H2O ® Ответ. Нет, не противоречит, так как планета Земля является открытой, а не изолированной системой и еженедельно получает от Солнца энергию, более чем в два раза превышающую все известные запасы энергии на Земле. Величина энтропии Солнца в результате происходящих на ней процессов (например, взрывов) существенно возрастает, в результате чего энтропия изолированной системы «Солнце – Земля – окружающая среда» увеличивается, что полностью согласуется со II законом термодинамики. Задача 4. Вычислите D r H0, D r S0 и D r G0 при стандартных условиях для реакции Fе2О3(тв) + 1.5 С(тв) → 2 Fе(тв) + 1.5 СО2(г). Решение. Для вычисления D r H0 и D r S0 воспользуемся первым следствием закона Гесса и значениями D f H0 и D f S0 для компонентов из приложения 1: D r H0 = (2×0 + 1.5×(–395.4)) – (–822 + 1.5×0) = –593.1 + 822 = D r S0 = (2×27.2 + 1.5×213.8) – (87.4 + 1.5×5.9) = 278.85 Дж/(моль×К). Рассчитаем D r G0 по уравнению D r G0 = D r H0 – TD r S0 при 298 К: D r G0 = 228 900 – 298×278.85 = 228 900 – 83 097,3 = 145.80 кДж/моль. Будет ли реакция протекать самопроизвольно при стандартных условиях? Поскольку при 298 К величина D r G0 имеет положительное значение, то реакция не должна протекать самопроизвольно при этой температуре.
При какой температуре становится возможным самопроизвольное протекание этой реакции, если предположить, что D r H0, D r S0 не зависят от температуры? Реакция может протекать самопроизвольно при условии, что D r G0 < 0, т.е. D r H0 – T D r S0 < 0. Последнее неравенство можно преобразовать к виду:
В рассматриваемом случае температура, начиная с которой становится возможным самопроизвольное протекание реакции, определяется неравенством
т.е. при T > 820,87 К. Таким образом, реакция будет протекать самопроизвольно при температурах выше 820,87 К. Задача 5. Не производя вычислений, установите знак DS0 следующих процессов: а) 2NH3(г) = N2(г) + 3H2(г) б) CO2(к) = CO2(г) в) 2NO(г) + O2(г) = 2NO2(г) г) 2H2S(г) + 3O2(г) = 2H2O(ж) + 2SO2(г) д) 2CH3OH(г) + 3O2(г) = 4H2O(г) + 2CO2(г) Решение. В реакции (а) 2 моля вещества в газообразном состоянии образуют 4 моля газов, следовательно, DS0 > 0. В реакции (б) 1 моль вещества в кристаллическом состоянии образует 1 моль газообразного вещества, следовательно, также DS0 > 0. В реакции (в) уменьшается как общее число молей, так и число молей газообразных веществ, так что DS0 < 0. В реакции (г) из 5 моль газообразных веществ образуются Задача 6. Не прибегая к расчетам, определите знаки D r H0, D r S0 и D r G0 для реакции: BaO(к) + CO2(г) = BaCO3(к), протекающей при температуре 298 К в прямом направлении. Как будет изменяться значение D r G0 с ростом температуры? Решение. Самопроизвольное протекание реакции указывает на то, что для нее D r G0 < 0. В результате реакции общее число частиц в системе уменьшается, причем расходуется газ CO2, а образуется кристаллическое вещество BaCO3; это означает, что система переходит в состояние с более высокой упорядоченностью, т. е. для рассматриваемой реакции D r S0 < 0. Таким образом, в уравнении D r G0 = D r H0 – T D r S0 величина D r G0 – отрицательная, а (– T D r S0) – положительная. Это возможно только в том случае, если D r H0 < 0. С ростом температуры положительное значение (– T D r S0) в уравнении возрастает, так что величина D r G0 будет становиться менее отрицательной. Вопросы для самоконтроля Основные понятия и законы термодинамики: 1) основные понятия термодинамики: окружающая среда, открытая, закрытая, изолированная системы, фаза, гетерогенная и гомогенная системы, термодинамический процесс, типы термодинамических процессов, энтальпия, энтропия, энергия Гиббса; 2) основные законы термодинамики: закон Гесса и следствия из него; I, II и III законы термодинамики. 2.4. Домашнее задание № 2 Задание 1. Вычислите D r H0, D r S0 и D r G0 при 150º С (для четных вариантов) и при стандартных условиях (для нечетных вариантов) для реакции (см. ваш вариант в табл. 2), если в реакции участвует 7,5 г вещества А. Задание 2. Является ли эта реакция экзо- или эндотермической? Протекает ли реакция самопроизвольно? Дайте пояснение. Задание 3. Определите температуру, при которой реакция находится в равновесии (Т р). Рассчитайте D r G0 при Т = Т р – 100, Т = Т р + 100 и постройте график зависимости D r G0 от температуры. Определите область температур самопроизвольного протекания реакции. Таблица 2
Окончание табл. 2
Лабораторная работа № 2 ИЗМЕРЕНИЕ ТЕПЛОВЫХ ЭФФЕКТОВ ХИМИЧЕСКИХ Цель работы. выполнение калориметрических измерений и термодинамических расчетов, связанных с энергетикой химических реакций. Опыт 1. Определение тепловых эффектов процесса растворения соли и гидроксида в воде Выполнение опыта. В стакан объемом 100 мл налейте 25 мл воды с помощью мерного цилиндра. На дно стакана поместите магнит и установите стакан на магнитную мешалку. Опустите термометр, погрузив его шарик в воду. Включите мешалку и настройте ее вращение на равномерное перемешивание раствора. Замерьте температуру Т 1 и внесите показания в отчет (табл. 3). Затем при работающей магнитной мешалке внесите в стакан 2 г мелких кристаллов аммония роданида (NH4SCN) или натрия нитрата (NaNO3), предварительно взвесив их на лабораторных весах, зафиксируйте температуру раствора Т 2. Аналогичный опыт проделайте, внося в стакан с 25 мл воды по 1 – 2 гранулы гидроксидов щелочных металлов (NaOH или KOH), при этом отметьте показания термометра. Результаты опыта внесите в табл. 3. Таблица 3
Задание. Запишите уравнение реакции процесса растворения соли (с образованием гидратов), заполните таблицу. Сделайте вывод на основании экспериментальных данных таблицы (отметьте тепловой эффект химических реакций). Опыт 2. Определение теплоты нейтрализации сильной кислоты сильным основанием и расчет энергии Гиббса реакции H+(ж) + OH– (ж) ® H2O(ж) ; D r H0(298 К) = –57 кДж/моль
Выполнение опыта. Соберите калориметрическую установку, которая состоит из наружного стакана, в который вставляется калориметрический стакан меньшей вместимости. Во избежание потерь теплоты между стаканами располагают пробковые прокладки. Стакан закрывают крышкой с отверстиями для термометра и воронки. На дно внутреннего стакана помещается магнит. Калориметрическую установку помещают на магнитную мешалку. В отверстия, имеющиеся в крышке, устанавливают термометр и воронку. В опыте используются растворы NaOH и HCl с концентрацией 1 моль/л. Для нейтрализации берут равные объемы (80, 90, 100 мл) растворов щелочи и кислоты. С помощью мерного цилиндра отмерьте заданный вам преподавателем объем раствора щелочи. Через воронку налейте этот объем в калориметрический стакан. Включите магнитную мешалку, настроив ее на равномерное перемешивание раствора, отметьте показания термометра и запишите температуру раствора щелочи Т 1 в отчет (табл. 4). Далее отмерьте цилиндром такой же объем раствора кислоты и при работающей мешалке через воронку быстро влейте кислоту в калориметрический стакан, зафиксируйте самую высокую температуру Т 2, которую покажет термометр после сливания растворов. Данные опыта сведите в таблицу. Таблица 4
Задание. Запишите уравнение реакции взаимодействия натрия гидроксида и соляной кислоты, термохимическое уравнение реакции нейтрализации; зарисуйте калориметрическую установку, заполните таблицу. На основании полученных экспериментальных данных проведите расчеты по следующей схеме. 1. Определите разность температур, D Т = Т 2 – Т 1. 2. Рассчитайте массу жидкости (m 2) в калориметрическом стакане (при расчете считать rраствора = 1 г/мл). 3. Вычислите суммарную теплоемкость системы: C = C1 m 1 + C2 m 2, где m 1 и m 2 – массы калориметрического стакана (указана на стакане) и раствора в стакане соответственно при условии, что удельная теплоемкость стекла C1 = 0,75·103 Дж/(кг·К), а удельную теплоемкость раствора C2 = 4,18·103 Дж/(кг·К). 4. Рассчитайте количество теплоты (Q), выделившейся в ходе реакции по уравнению Q = C ×D Т. 5. Определите количество молей нейтрализованной кислоты (щелочи) n или количество молей полученной воды ( 6. Вычислите энтальпию реакции нейтрализации по уравнению
7. Рассчитайте изменение энтропии (D r S0, Дж/моль·К) для реакции нейтрализации по первому следствию закона Гесса, при расчете пользуйтесь данными приложения 3. 8. Вычислите энергию Гиббса реакции нейтрализации по уравнению D r G0 = D r H0 – T D r S0 (кДж/моль). 9. Рассчитайте погрешность определения энтальпии реакции нейтрализации:
Сделайте вывод. Укажите, экзо- или эндотермическим является процесс нейтрализации сильной кислоты сильным основанием. Объясните уменьшение, а не увеличение энтропии в ходе реакции. Отметьте соответствие найденной вами величины D r G0 самопроизвольному течению реакции нейтрализации.
3. ХИМИЧЕСКАЯ КИНЕТИКА Теоретическая часть Раздел физической химии, изучающий механизмы химических реакций и скорости их протекания, называют химической кинетикой. Механизмом химических реакций называется совокупность всех элементарных стадий реакции при переходе вещества из начального в конечное состояние. Например, для реакции аА + вВ Þ аА’ + вВ’=> cAB Þ pP, где А и В – реагенты; А’ и В’ – промежуточные соединения или интермедиаты; Р – продукт реакции; а, в, с, р – стехиометрические коэффициенты; установление механизма будет заключаться в определении всех возможных промежуточных соединений и элементарных стадий реакции при получении конечного продукта. Молекулярность реакции равна общему числу частиц (молекул, радикалов, атомов), принимающих участие в элементарной реакции или элементарном акте реакции. Молекулярность всегда целочисленна, положительна и меньше либо равна 3. Различают моно -, би- и три молекулярные реакции. а) мономолекулярные реакции наблюдаются при распаде молекул, при цис-, транс-изомеризации, например:
б) бимолекулярные реакции осуществляются путем столкновения двух молекул в газовой фазе: K· + HBr => KBr + H· или Cl.·+ Cl.·=> Cl2 или в растворах: CH3I+C2H5ONa=> CH3 – O – C2H5+NaI, а также при димеризации алкинов, диенов, например: 2HCºCH=> HCºC – CH=CH2 в) тримолекулярные реакции наблюдаются при одновременном соударении трех молекул: 2NO+O2=> 2NO2 2NO+Cl2=> 2NOCl Тримолекулярные реакции встречаются редко, так как вероятность одновременного столкновения трех частиц достаточно мала. Скорость химической реакции определяется как количество вещества (n,моль), превращенного (образовавшегося или распавшегося) в единицу времени (t, с), в единице реакционного пространства (V, л).
Поскольку количество вещества в единице объема есть выражение молярной концентрации, то можно сказать, что скорость гомогенной реакции определяется изменением концентрации реагентов или продуктов реакции за единицу времени.
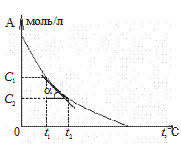
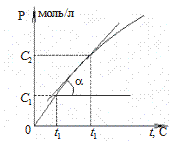
Примеры гомогенных реакций: 2SO2(газ) + O2(газ) ® 2SO3(газ) AgNO3(раствор) + NaCl(раствор) ® AgCl¯ + NaNO3(раствор) Изменение концентраций исходных веществ или концентрации продукта реакции в зависимости от времени можно представить графически: а) по изменению концентрации реагентов, б) по изменению концентрации продуктов реакции аА + вВ Þ аА’ + вВ’=> cAB Þ рP
а б D t = t 2 – t 1 > 0 D t = t 2 – t 1 > 0 D C = C 2 – C 1 < 0 D C = C 2 – C 1 > 0
Таким образом, в общем случае:
истинная скорость (или скорость в точке) определяется как производная по концентрации от времени:
Для гетерогенных реакций, протекающих на границе раздела фаз, важной величиной является площадь поверхности раздела фаз (S). Поэтому под скоростью гетерогенной реакции понимают изменение концентрации реагирующих веществ за определенный промежуток времени на единице поверхности раздела фаз:
Примеры гетерогенных реакций: Na(тв) + H2O(ж) ® NaOH(раствор) + 1/2H2(газ) Cu(тв) + 4HNO3(конц. раствор) ® Cu(NO3)2 (раствор) + 2NO2 (газ) + 2 H2O(ж) Скорость химической реакции определяется многими факторами: · природой вещества, дисперсностью, наличием дефектов в кристаллических структурах; · концентрациями реагирующих веществ; · температурой; · наличием катализатора; · давлением (для реакций, протекающих в газовой фазе). Изучением влияния концентрации на скорость химических реакций в растворах занимался Н.Н. Бекетов, в газовых фазах К. Гульдберг и Вааге (1862 – 1867гг.). Ими и был сформулирован основной постулат химической кинетики – закон действующих масс (ЗДМ).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 530; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.163.233 (0.013 с.) |

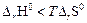 , или
, или 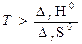 .
.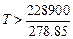 ,
,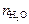 ), учитывая заданную молярную концентрацию основания и кислоты (1 моль/л) и объемы растворов.
), учитывая заданную молярную концентрацию основания и кислоты (1 моль/л) и объемы растворов.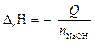 , кДж/моль.
, кДж/моль.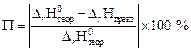 .
.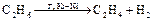
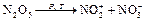
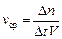

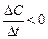
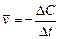
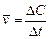
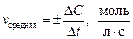 .
.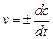 .
.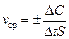 .
.


