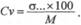Значение среднего квадратического отклонения

1. Среднее квадратическое отклонение характеризует разброс вариант
относительно средней величины, т. е. характеризует колеблемость вариацион­
ного ряда.

Чем больше среднее квадратическое отклонение, тем степень разнообра­зия данного ряда выше.

2. Среднее квадратическое отклонение используется для сравнительной
оценки степени соответствия средней арифметической величины тому вариа­
ционному ряду, для которого она вычислена.

Вариации массовых явлений подчиняются закону нормального распреде­ления. Кривая, отображающая это распределение, имеет вид плавной колоколо-образной симметричной кривой (кривая Гаусса). Согласно теории вероятности в явлениях, подчиняющихся закону нормального распределения, между значе­ниями средйей арифметической и среднего квадратического отклонения суще­ствует строгая математическая зависимость. Теоретическое распределение ва­риант в однородном вариационном ряду подчиняется правилу трех сигм.

Рис. 1. Теоретическая кривая нормального распределения

Установлено, что при нормальном распределении признака:

Если в системе прямоугольных координат на оси абсцисс отложить зна­чения количественного признака (варианты), а на оси ординат — частоты встречаемости вариант в вариационном ряду, то по сторонам от средней ариф­метической равномерно располагаются варианты с большими и меньшими зна­чениями (рис. 1).

Установлено, что при нормальном распределении признака:

- 68,3% значений вариант находится в пределах М± 1σ;

- 95,5% значений вариант находится в пределах М± 2σ;

- 99,7% значений вариант находится в пределах А/± Зσ.

Если к средней арифметической величине прибавить или отнять одну сигму (M± 1σ), то при нормальном распределении признака в статистической совокупности в этих границах будет находиться не менее 68,3% всех вариант. В пределах М± 2σ будет заключено 95,5% всех наблюдений. Если к средней при­бавить или отнять три сигмы (М± Зσ), то в этих границах будут расположены 99,7% всех вариант изучаемой совокупности.

В нашем примере (табл.7) М = 20 дней, σ = 1,6 дня. В пределах М±1σ находится 65 вариант, что составляет 68,4% всех наблюдений

Такое распределение вариант позволяет считать, что данный вариационный ряд является однородным, а средняя арифметическая величина — типичной.

3. Среднее квадратическое отклонение позволяет установить значения нормы для клинико-биологических показателей. В медицине интервал М ± 1σ обычно принимается за пределы нормы для изучаемого явления. Отклонение оцениваемой величины от средней арифметической больше, чем на 1с указыва­ет на отклонение изучаемого параметра от нормы.

4. В медицине правило трех сигм применяется в педиатрической практике для индивидуальной оценки уровня физического развития детей (метод сиг-мальных отклонений), для разработки стандартов детской одежды, обуви, школьной мебели и т. д.

5. Среднее квадратическое отклонение необходимо для характеристики
степени разнообразия изучаемого признака и вычисления ошибки средней
арифметической величины.

Коэффициент вариации

Среднее квадратическое отклонение позволяет установить степень ти­пичности средней, пределы рассеяния ряда, сравнить колеблемость нескольких рядов распределения. Величина среднего квадратического отклонения обычно используется для сравнения колеблемости однотипных рядов, т. е. рядов, харак­теризующих одинаковый признак (например, рост мальчиков и рост девочек).

Если сравниваются два ряда с разными признаками (рост и масса тела, средняя длительность лечения в стационаре и кратность заболевания и т. д.), то непосредственное сопоставление размеров с невозможно, так как среднеквад-ратическое отклонение (σ) — именованная величина, имеющая единицу изме­рения

Для сравнения колеблемости двух средних величин, выраженных в раз­личных единицах измерения, используется относительная величина — коэффи­циент вариации (Cv).

Коэффициент вариации вычисляется по формуле:

Чем больше коэффициент вариации, тем большая изменчивость данного ряда. Чем он меньше, тем меньше колеблемость, тем однороднее вариационный ряд, тем типичнее средняя арифметическая величина. Если коэффициент ва­риации менее 10%, признак характеризуется слабым разнообразием; если ко­эффициент вариации от 10 до 20% — средним разнообразием; более 20% — сильным разнообразием. Величина коэффициента вариации более 30% свиде­тельствует о качественной неоднородности совокупности.

Пример 8: по данным специального исследования средний рост мальчи­ков 7 лет в городе N составил 117,7 см (с = 5,1 см), а средний вес — 21,7 кг (σ = 2,4 кг). Оценить колеблемость роста и веса путем сравнения средних квад-ратических отклонений нельзя, так как вес и рост — величины именованные, выраженные в разных единицах измерения. Поэтому используется относитель­ная величина — коэффициент вариации:

Сравнение коэффициентов вариации роста (4,3%) и веса (11,2%) показы­вает, что вес имеет более высокий коэффициент вариации, следовательно, явля­ется менее устойчивым признаком, чем рост.

Применение средних величин

Средние величины широко применяются в повседневной работе меди­цинских работников, в частности:

1) для характеристики физического развития: рост, вес, окружность груди, динамометрия и т. д.;

2) оценки состояния здоровья человека путем анализа физиологиче­ских, биохимических параметров организма (уровня артериального давле­ния, частоты сердечных сокращений, температуры тела, уровня биохимических показателей, содержания гормонов и т. д.);

3) анализа деятельности медицинских организаций, например:

 

- при анализе работы стационаров вычисляются показатели; среднее число дней работы койки в году, средняя длительность пребывания больного на койке и т. д.;

- при оценке работы амбулаторно-поликлинических организаций — сред­нее число посещений на одного жителя в год, средняя продолжительность одного случая заболеваемости с временной утратой трудоспособности и т. д.;

4) для оценки работы врачей: рассчитываются среднее число посещений
на одного врача, среднее число хирургических операций, среднечасовая нагрузка
врача на приеме в поликлинике, среднее число лабораторных исследований и т. д.