Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предназначено для иностранных учащихся медицинских учебных заведений.Содержание книги
Поиск на нашем сайте
Предназначено для иностранных учащихся медицинских учебных заведений. УДК 614.1 (075.8) ББК 51.1 (2) я 73
МЕДИЦИНСКАЯ СТАТИСТИКА Статистика — это наука, которая изучает количественную сторону массовых общественных явлений и процессов в неразрывной связи с их качественными особенностями в конкретных условиях места и времени. Она позволяет выявить закономерности массовых явлений, используя обобщающие показатели. Статистика является универсальной наукой. Статистический метод широко применяется в различных областях науки, техники, народного хозяйства. Выделяют математическую, физическую, экономическую, социальную статистику и т. д. Наибольший интерес для врачей представляет социальная статистика, изучающая социальные явления и процессы. Одна из отраслей социальной статистики — медицинская статистика. Медицинская статистика — отрасль статистической науки, которая изучает вопросы, связанные с медициной, гигиеной, здравоохранением. Задачами медицинской статистики являются: 1. Изучение состояния здоровья населения в целом или отдельных его групп, выявление количественных характеристик общественного здоровья. 2. Выявление связей между показателями здоровья и различными факторами природной и социальной среды, оценка влияния этих факторов на здоровье населения. 3. Изучение данных о сети организаций здравоохранения, медицинских кадрах, анализ их деятельности. 4. Оценка эффективности (медицинской, социальной, экономической) проводимых лечебных, профилактических, противоэпидемических мероприятий и здравоохранения в целом. 5. Использование статистических методов в клинических, социально-медицинских и экспериментальных исследованиях. Выделяют три раздела медицинской статистики: 1. Статистика здоровья населения — изучает состояние здоровья населения в целом или его отдельных групп (путем сбора и статистического анализа данных о численности и составе населения, его воспроизводстве, естественном движении, физическом развитии, распространенности различных заболеваний, продолжительности жизни и т. д.). Оценка показателей здоровья проводится в сопоставлении с общепринятыми оценочными уровнями, уровнями, полученными по различным регионам, и в динамике. 2. Статистика здравоохранения — решает вопросы сбора, обработки и анализа статистической информации о сети организаций здравоохранения (их размещении, оснащении, деятельности) и кадрах (о численности врачей, среднего и младшего медицинского персонала, распределении их по специальности, стажу работы, переподготовке и т. д.). При анализе деятельности медицинских организаций полученные данные сопоставляются с нормативными уровнями, а также уровнями, полученными по другим регионам, и в динамике. 3. Клиническая статистика — это использование статистических методов при обработке результатов клинических, экспериментальных и лабораторных исследований. Она позволяет с количественной точки зрения оценить достоверность результатов исследования и решить ряд других задач (определение необходимого числа наблюдений при выборочном исследовании, формирование экспериментальной и контрольной групп, изучение корреляционных и регрессионных связей, устранение качественной неоднородности групп и т. д.). Статистика применяется для изучения не отдельных, единичных, а массовых общественных явлений в целях определения общих закономерностей, присущих изучаемому явлению. Эти закономерности проявляются, как правило, в массе наблюдений, то есть при изучении статистической совокупности. СТАТИСТИЧЕСКАЯ СОВОКУПНОСТЬ Объектом любого статистического исследования является статистическая совокупность. Статистическая совокупность — это группа относительно однородных элементов, взятых вместе в конкретных границах пространства и времени и обладающих признаками сходства и различия. Объектом статистического исследования в медицине и здравоохранении могут быть различные контингенты населения (население в целом или его отдельные возрастные, социальные, профессиональные, территориальные группы, больные, умершие, родившиеся и др.), медицинские организации, медицинские кадры, объекты санитарного надзора и т. д. Статистическая совокупность состоит из отдельных, единичных наблюдений. Единица наблюдения — это каждый первичный элемент, составляющий статистическую совокупность и являющийся носителем признаков, подлежащих учету. Единица наблюдения определяется целью и задачами статистического исследования, а также избранным объектом изучения. Так, при изучении больничной летальности единицей наблюдения будет умерший в стационаре; при изучении общей заболеваемости населения — первичное обращение по поводу данного заболевания в данном календарном году; при изучении эффективности нового метода лечения — каждый больной, получавший лечение и т. п. Четкое определение единицы наблюдения необходимо для правильного проведения статистического исследования. Единицы наблюдения имеют признаки сходства и различия. Признаки сходства служат основанием для объединения единиц наблюдения в совокупность. Признаки, по которым различаются элементы статистической совокупности, подлежат регистрации и называются учетными признаками. Учетные признаки по характеру могут быть качественные (атрибутивные, описательные) и количественные (выраженные числом). К качественным признакам относятся: пол. профессия, нозологическая форма заболевания, исход заболевания и т. п. Количественными признаками являются: рост, масса тела, возраст, продолжительность болезни, длительность лечения в стационаре, уровень белка в моче и др. По роли в изучаемой совокупности учетные признаки делятся на факторные и результативные. Факторные — это признаки, под влиянием которых изменяются другие, зависящие от них признаки. Результативные — это признаки, зависящие от факторных признаков. С изменением величины факторного признака происходит изменение результативного. Так, с увеличением возраста ребенка увеличивается его рост, с увеличением охвата детей профилактическими прививками против кори снижается заболеваемость корью и т. п. ОРГАНИЗАЦИЯ СТАТИСТИЧЕСКОГО ИССЛЕДОВАНИЯ Чтобы получить представление о том или ином явлении, сделать выводы, необходимо провести статистическое исследование. Статистическое исследование позволяет определить размер, уровень изучаемого явления, выявить его закономерности. Предметом статистического исследования в здравоохранении и медицине могут быть здоровье населения, организация медицинской помощи, разделы деятельности лечебно-профилактических организаций (учреждений), факторы внешней среды, оказывающие влияние на состояние здоровья, профилактические мероприятия. При проведении медико-статистического исследования могут быть использованы два типа методического подхода: 1) изучение интенсивности явления в среде, распространенности явления, выявление тенденций состояния здоровья населения; 2) проведение строго спланированных исследований по изучению отдельных факторов без выявления интенсивности явления в среде. Исследования первого типа проводятся на генеральных совокупностях или достаточно больших по численности выборочных совокупностях, позволяющих получить интенсивные показатели и обоснованно перенести полученные данные на всю генеральную совокупность. Второй тип медико-статистических исследований проводится с целью выявления новых факторов, изучения неизвестных или малоизученных причинно-следственных связей. Эти исследования, как правило, проводятся на небольших по численности совокупностях. Сбор материала (статистическое наблюдение). Простые (однофакторные). Групповые. Комбинационные. В простых таблицах представлено числовое распределение материала по одному признаку (фактору) (табл. 2). Простая таблица содержит обычно простой перечень и итог по всей совокупности изучаемого явления. Она не содержит никаких фуппировок. Эта таблица может быть территориальной, хронологической или перечневой. В групповых таблицах представлено сочетание двух признаков. Групповая таблица может иметь и больше признаков, однако сочетаться они должны только попарно (табл. 3). Таблица 2 Распределение умерших в больнице Н. по возрасту за 2...г.
Таблица 3 Распределение умерших в больнице Н. по полу и возрасту за 2...Г.
В комбинационных таблицах дается распределение материала по трем и более взаимосвязанным признакам (табл. 4). В одну комбинационную таблицу не следует включать много признаков, так как это приводит к значительному дроблению материала и затрудняет анализ данных. Таблица 4 Распределение умерших в больнице Н. при разных заболеваниях по возрасту и полу за 2...г.
Каждая таблица должна иметь заголовок, отражающий ее содержание. Правильно оформленным является заголовок таблицы, если в нем содержатся ответы на следующие вопросы: что, где. когда изучается? (Например, летальность в стационарах города N. в 2002 году). Внутри таблицы все графы также должны иметь четкие краткие названия. При заполнении таблицы все клетки ее должны содержать соответствующие числовые данные. В оставшихся незаполненными клетках таблицы ставится прочерк (—), а при отсутствии сведений проставляется (н.с.) или многоточие (...). После заполнения таблицы в нижнем горизонтальном ряду и в последнем справа вертикальном столбце подводятся итоги вертикальных граф и горизонтальных строк. Существует ручная обработка данных и обработка с использованием ЭВМ. В исследованиях, имеющих небольшой объем наблюдений, сводка проводится вручную. Все учетные документы раскладываются на группы в соответствии с шифром признака. Далее проводится подсчет и запись данных в соответствующую клетку таблицы. В настоящее время при сортировке и сводке материала широко используются ЭВМ, которые позволяют не только отсортировать материал по изучаемым признакам, разнести по необходимым таблицам, рассчитать статистические величины, но и применить сложные методы статистического многомерного анализа, обеспечить создание банков данных. Следует отметить, что никакая математико-статистическая обработка с использованием ЭВМ не может исправить дефектов первичного медицинского учета, неправильной группировки данных и несовершенной сводки их в статистические таблицы. Чтобы грамотно провести анализ, необходимо знать сущность изучаемого явления или процесса. Прежде чем приступить к составлению таблиц, надо сопоставить признаки, выявить их взаимосвязи и взаимозависимости между собой, что требует логического осмысления явления. Четвертый этап — статистический анализ. На этом этапе вычисляются статистические величины (относительные величины, средние величины, индек- сы), осуществляется их оценка, проводится сопоставление полученных данных во времени и пространстве, изучается динамика, тенденции, устанавливаются связи между явлениями, даются прогнозы и т. д. Анхчиз предполагает интерпретацию полученных данных, оценку достоверности результатов исследования. В заключение делаются выводы и вносятся предложения. Пятый этап — литературная обработка — заключительный. Он предполагает окончательное оформление результатов статистического исследования. Результаты могут быть оформлены в виде статьи, отчета, доклада, диссертации и др. Для каждого вида оформления существуют определенные требования, которые должны соблюдаться при литературной обработке результатов статистического исследования. Результаты медико-статистического исследования внедряются в практику здравоохранения. Возможны различные варианты использования результатов исследования: ознакомление с результатами широкой аудитории медицинских и научных работников; подготовка инструктивно-методических документов: оформление рационализаторского предложения и другие. СТАТИСТИЧЕСКИЕ ВЕЛИЧИНЫ Для сравнительного анализа данных медико-социального исследования используются статистические величины: абсолютные, относительные, средние. Абсолютные величины Абсолютные величины, полученные в сводных таблицах в ходе статистического исследования, отражают абсолютный размер явления (число лечебно-профилактических организаций, число коек в больнице, численность населения, число умерших, родившихся, заболевших и т. д.). Хотя абсолютные цифры и имеют свое познавательное значение, применение их ограничено. Ряд статистических исследований завершается получением абсолютных величин. Иногда они могут быть использованы для анализа изучаемого явления, например, при изучении редких явлений, если надо знать точный абсолютный размер явления, при необходимости обратить внимание на отдельные случаи этого явления. При малом числе наблюдений, когда не требуется определения закономерности, также могут использоваться абсолютные числа. В значительной части случаев абсолютные величины не могут быть использованы для сравнения с данными других исследований. Для этого служат относительные и средние величины. Относительные величины Относительные величины (показатели, коэффициенты) получаются в результате отношения одной абсолютной величины к другой. Наиболее часто используются следующие показатели: интенсивные, экстенсивные, соотношения, наглядности. Интенсивные — это показатели частоты, интенсивности явления в среде, продуцирующей данное явление. Они показывают, как часто данное явление встречается в среде. В здравоохранении изучаются заболеваемость, смертность, инвалидность, рождаемость и другие показатели здоровья населения. Средой, в которой происходят процессы, является население в целом или его отдельные группы (возрастные, половые, социальные, профессиональные и др.). В медико-статистических исследованиях при изучении общественного здоровья явление представляет собой как бы продукт среды. Например, население (среда) и заболевшие (явление); больные (среда) и умершие (явление) и т. д.
Величина основания выбирается в соответствии с величиной показателя — 100. 1000, 10000, 100000. — и в зависимости от этого показатель выражается в процентах, промилле, продецимилле, просантимилле. В статистике при вычислении: - санитарно-демографических показателей (смертность, рождаемость, младенческая смертность, естественный прирост населения и др.) за основание обычно принимают 1000; - общей и первичной заболеваемости — 100000 населения; - первичной инвалидности — 10000 населения; - показателей заболеваемости с временной нетрудоспособностью — 100 работающих; - показателей летальности — 100 заболевших (или выбывших из стационара). Пример 1: в Иране в 2000 г. проживало 70330 тыс. жителей, в течение года умерло 356000 человек.
Интенсивные показатели могут быть общими и специальными. Общие интенсивные показатели характеризуют явление в целом, например, общие показатели рождаемости, смертности, заболеваемости, вычисленные ко всему населению административной территории, общий показатель летальности по больнице в целом и т. д. Специальные (погрупповые) интенсивные показатели применяются для характеристики частоты явления в различных группах (заболеваемость по полу, возрасту, смертность среди детей в возрасте до 1 года, летальность по отдельным нозологическим формам в разных возрастных группах и т. д.). Пример 2: в Республике Беларусь в 2001 г. было зарегистрировано 113400 травм и отравлений у детей. Численность детского населения — 1830000.
Интенсивные показатели применяются: - для определения уровня, частоты, распространенности явления; - для сравнения частоты явления в различных совокупностях; - для изучения изменений частоты явления в динамике. Экстенсивные — это показатели удельного веса, структуры, характеризуют распределение явления на составные части, его внутреннюю структуру. Эти показатели показывают, какую долю от общего числа явления составляет та или иная часть явления, входящая в общее число. Экстенсивные показатели вычисляются делением части явления на целое и выражаются в процентах или долях единицы.
Пример 3: в Ливане в 2000 г. из всей численности населения 3496000 человек в городах проживало 3146400 жителей.
Экстенсивные показатели используются для определения структуры явления и сравнительной оценки соотношения составляющих его частей. Экстенсивные показатели взаимосвязаны между собой, так как их сумма всегда равна 100%. Так, при изучении структуры заболеваемости удельный вес отдельной нозологической формы заболевания может возрасти: - при истинном росте числа заболеваний; - при одном и том же его числе, если число других заболеваний снизилось; - при снижении числа данного заболевания, если уменьшение числа других заболеваний происходит более быстрыми темпами. При анализе экстенсивный показатель следует применять с осторожностью и помнить, что им пользуются только для характеристики состава (структуры) явления в данный момент времени и в данном месте. Примеры экстенсивного показателя: лейкоцитарная формула; структура населения по полу, возрасту, социальному положению; структура заболеваний по нозологическим формам; структура причин смерти и пр. Показатели соотношения представляют собой соотношение двух самостоятельных, независимых друг от друга, качественно разнородных величин, сопоставляемых только логически. К показателям соотношения относятся: показатели обеспеченности населения врачами, средними медицинскими работниками, больничными койками, а также показатели, отражающие число лабораторных исследований на одного врача число переливаний крови на одного оперированного больного и др. Техника вычисления показателя соотношения та же, что и интенсивного, однако при расчете интенсивного показателя число, стоящее в числителе, входит в состав знаменателя, тогда как в показателе соотношения числитель и знаменатель различны по характеру (т. е. являются разнородными величинами).
Пример 4: в Польше с численностью населения 38605 тыс. жителей в медицинских организациях в 2000 г. работали 88000 врачей.
Показатели наглядности применяются с целью более наглядного и доступного сравнения статистических величин. Показатели наглядности представляют удобный способ преобразования абсолютных, относительных или средних величин в легкую для сравнения форму. Они применяются также в тех случаях, когда необхЪдимо показать направление процесса, тенденции, не показывая уровня или истинных размеров явления. При вычислении этих показателей одна из сравниваемых величин приравнивается к 100 (или 1), а остальные величины пересчитываются соответственно этому числу.
Пример 5: численность населения Иордании составила в 1998 г. — 6304 тыс. человек, в 1999 г. — 6482 тыс. человек, в 2000 г. — 4913 тыс. человек (табл. 5). За 100 принимаем численность населения Иордании за 1998 г. (как наиболее отдаленный в историческом аспекте). Таблица 5 Динамика численности населения Иордании за 1998-2000 гг.
Показатели наглядности используются чаще всего для сравнения данных в динамике, чтобы представить закономерности изучаемого явления в более наглядной форме. При пользовании относительными величинами могут быть допущены некоторые ошибки. Приведем наиболее частые из них. - иногда судят об изменении частоты явления на основе экстенсивных показателей, которые характеризуют структуру явления, а не его интенсивность; - нельзя складывать и вычитать статистические показатели, которые рассчитаны из совокупностей, имеющих разную численность, ибо это приводит к грубым искажениям показателя; - при расчете специальных показателей следует правильно выбирать знаменатель; например, показатель послеоперационной летальности необходимо рассчитывать по отношению к оперированным, а не всем больным; - при анализе показателей следует учитывать фактор времени, нельзя сравнивать между собой показатели, вычисленные за различные периоды времени: например, показатель заболеваемости за год и за полугодие, что может привести к ошибочным суждениям; - нельзя сравнивать между собой общие интенсивные показатели, вычисленные из неоднородных по составу совокупностей, поскольку неоднородность состава среды может влиять на величину интенсивного показателя. Средние величины Единицы наблюдения статистической совокупности могут характеризоваться количественными признаками. Каждый изучаемый количественный признак принимает разные значения у различных единиц статистической совокупности, он меняется в своем значении от одной единицы совокупности к другой. Это различие между единицами совокупности называется вариациями. Числовое значение признака для той или иной единицы совокупности называют вариантой и обозначают буквой V или X. Для анализа количественных признаков рассчитывают средние величины. Средние величины дают обобщающую характеристику статистической совокупности по определенному изменяющемуся количественному признаку. Средняя величина характеризует весь ряд наблюдений одним числом, выражающим общую меру изучаемого признака. Она нивелирует случайные отклонения отдельных наблюдений и дает типичную характеристику количественного признака. Важнейшим условием при вычислении средних величин является качественная однородность совокупности, для которой они рассчитываются. Только в этом случае она будет объективно отображать характерные особенности изучаемого явления. Второе требование заключается в том, что средняя величина только тогда выражает типичные размеры признака, когда она основывается на массовом обобщении изучаемого признака, т. е. рассчитывается на достаточном числе наблюдений. Средние величины получают из рядов распределения (вариационных рядов). Вариационный ряд — ряд однородных статистических величин, характеризующих один и тот же количественный учетный признак, отличающихся друг от друга по своей величине и расположенных в определенном порядке (возрастания или убывания). Элементами вариационного ряда являются: • Варианта — V(X) — числовое значение изучаемого меняющегося ко ■ Частота — р (pars), или f (frequency) — повторяемость вариант в вариационном ряду, показывающая, как часто встречается та или иная варианта в составе данного ряда. • Общее число наблюдений — п (numerus) — сумма всех частот (где п Виды вариационных рядов: 1. В зависимости от значения варианты (V): прерывные (дискретные) Вариационные ряды могут быть прерывные (дискретные), состоящие из целых чисел, и непрерывные, когда значения вариант выражены дробным числом. В прерывных рядах смежные варианты отличаются друг от друга на целое число, например: число ударов пульса, число дыханий в минуту, число детей в семье, число дней лечения и т. д. В непрерывных рядах варианты могут отличаться на любые дробные значения единицы, например, при изучении веса взрослых можно ограничиться килограммами, а при изучении веса новорожденных — граммами. 2. В зависимости от частоты встречаемости признака (р): простой, Простой ряд — каждая варианта встречается один раз, т. е. частоты равны единице (р=1). Обычный ряд — варианты встречаются более одного раза (р>1). Сгруппированный ряд — варианты объединены в группы по их величине в пределах определенного интервала с указанием частоты повторяемости всех вариант, входящих в группу. Сгруппированный вариационный ряд используют при большом числе наблюдений и большом размахе крайних значений вариант. 3. В зависимости от числа наблюдений (п): а) четные и нечетные; б) большой (при числе наблюдений больше 30, п >30), малый (если число При изучении достаточно большого числа наблюдений в распределении вариант в вариационных рядах имеются определенные закономерности. 1. Большинство вариант часто располагаются в средней части вариационного ряда. 2. Распределение вариант в обе стороны от этого максимума более или менее симметрично. 3. Частоты вариант постепенно убывают к краям вариационного ряда. Виды средних величин В медицинской практике наиболее часто используются следующие средние величины: мода, медиана, средняя арифметическая. Реже применяются другие средние величины: средняя геометрическая (при обработке результатов титрования антител, токсинов, вакцин); средняя квадратическая (при определении среднего диаметра среза клеток, результатов накожных иммунологических проб); средняя кубическая (для определения среднего объема опухолей), средняя прогрессивная и др. Мода (Мо) — величина признака, чаще других встречающаяся в совокупности. За моду принимают варианту, которой соответствует наибольшее количество частот вариационного ряда. Медиана (Me) — величина признака, занимающая срединное положение в вариационном ряду. Она делит вариационный ряд на две равные части. Для определения медианы следует найти ее порядковый номер в вариационном ряду по формуле, а затем установить ее числовое значение:
Зная порядковый номер медианы в вариационном ряду, определяют ее числовое значение. На величину моды и медианы не оказывают влияния числовые значения крайних вариант, имеющихся в вариационном ряду. Мода и медиана применяются в медицинской статистике относительно редко. Более точно характеризует вариационный ряд средняя арифметическая величина, которая чаще других средних величин используется в медицинской статистике. Средняя арифметическая (М, или X) — рассчитывается на основе всех числовых значений изучаемого признака. В простом вариационном ряду, где варианты встречаются только по одному разу, вычисляется средняя где V — числовые значения вариант, п — число наблюдений, Σ — знак суммы. В обычном вариационном ряду вычисляется средняя арифметическая взвешенная по формуле: где V — числовые значения вариант, р — частота встречаемости вариант, п — число наблюдений, Σ — знак суммы. Таблица 6 Определение средней длительности лечения больных в специализированном отделении больницы за 2... г.
В приведенном примере 6 (табл.6) модой является варианта, равная 20 дням, поскольку она повторяется чаще других — 29 раз. Мо = 20 дней. Порядковый номер медианы приходится на 48-ю варианту
Средняя арифметическая, рассчитанная по формуле, равна 20 дням. Средняя величина — именованная величина, она выражается в тех же единицах измерения, что и варианта (днях, килограммах, метрах и т. д.) Средние величины являются важными обобщающими характеристиками совокупности. Однако за ними скрываются индивидуальные значения признака. Средние величины не показывают изменчивости, колеблемости признака. Если вариационный ряд более компактен, менее рассеян и все отдельные значения расположены вокруг средней, то средняя величина дает более точную характеристику данной совокупности. Если вариационный ряд растянут, отдельные значения значительно отклоняются от средней, т. е. имеется большая вариабельность количественного признака, то средняя менее типична, недостаточно точно отражает в целом весь ряд. Одинаковые по величине средние могут быть получены из рядов с различной степенью рассеяния. Так, например, средняя длительность лечения больных в специализированном отделении больницы также будет равна 20 дням, если все больные находились на стационарном лечении по 20 дней. Обе вычисленные средние равны между собой, но получены из рядов с разной степенью разнообразия вариант. Следовательно, для характеристики вариационного ряда, помимо средней величины, необходима другая характеристика, позволяющая оценить степень его разнородности. Простыми показателями, характеризующими разнообразие признака в изучаемой совокупности, являются лимит и амплитуда. Лимит — это минимальное и максимальное значения количественного тризнака. В примере 6 лимит = 16 и 24 дня. Амплитуда — это разность между наибольшим и наименьшим значени-гм вариант (Vmax -- Vmin). В примере 6 амплитуда = 24 - 16 = 8 дней. Чем меньше амплитуда колебания ряда (степень рассеяния ряда), тем бо-iee точно его будет характеризовать средняя арифметическая. Однако лимит и амплитуда не учитывают значений вариант внутри ряда. Коэффициент вариации Среднее квадратическое отклонение позволяет установить степень типичности средней, пределы рассеяния ряда, сравнить колеблемость нескольких рядов распределения. Величина среднего квадратического отклонения обычно используется для сравнения колеблемости однотипных рядов, т. е. рядов, характеризующих одинаковый признак (например, рост мальчиков и рост девочек). Если сравниваются два ряда с разными признаками (рост и масса тела, средняя длительность лечения в стационаре и кратность заболевания и т. д.), то непосредственное сопоставление размеров с невозможно, так как среднеквад-ратическое отклонение (σ) — именованная величина, имеющая единицу измерения Для сравнения колеблемости двух средних величин, выраженных в различных единицах измерения, используется относительная величина — коэффициент вариации (Cv). Коэффициент вариации вычисляется по формуле:
Чем больше коэффициент вариации, тем большая изменчивость данного ряда. Чем он меньше, тем меньше колеблемость, тем однороднее вариационный ряд, тем типичнее средняя арифметическая величина. Если коэффициент вариации менее 10%, признак характеризуется слабым разнообразием; если коэффициент вариации от 10 до 20% — средним разнообразием; более 20% — сильным разнообразием. Величина коэффициента вариации более 30% свидетельствует о качественной неоднородности совокупности. Пример 8: по данным специального исследования средний рост мальчиков 7 лет в городе N составил 117,7 см (с = 5,1 см), а средний вес — 21,7 кг (σ = 2,4 кг). Оценить колеблемость роста и веса путем сравнения средних квад-ратических отклонений нельзя, так как вес и рост — величины именованные, выраженные в разных единицах измерения. Поэтому используется относительная величина — коэффициент вариации:
Сравнение коэффициентов вариации роста (4,3%) и веса (11,2%) показывает, что вес имеет более высокий коэффициент вариации, следовательно, является менее устойчивым признаком, чем рост. Применение средних величин Средние величины широко применяются в повседневной работе медицинских работников, в частности: 1) для характеристики физического развития: рост, вес, окружность груди, динамометрия и т. д.; 2) оценки состояния здоровья человека путем анализа физиологических, биохимических параметров организма (уровня артериального давления, частоты сердечных сокращений, температуры тела, уровня биохимических показателей, содержания гормонов и т. д.); 3) анализа деятельности медицинских организаций, например:
- при анализе работы стационаров вычисляются показатели; среднее число дней работы койки в году, средняя длите
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 286; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.009 с.) |












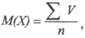 арифметическая простая по формуле:
арифметическая простая по формуле:
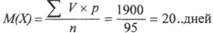
 , числовое значение которой равно 20. Me = 20 дней.
, числовое значение которой равно 20. Me = 20 дней.