Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предельные размеры определяются через предельные отклонения.Содержание книги
Поиск на нашем сайте
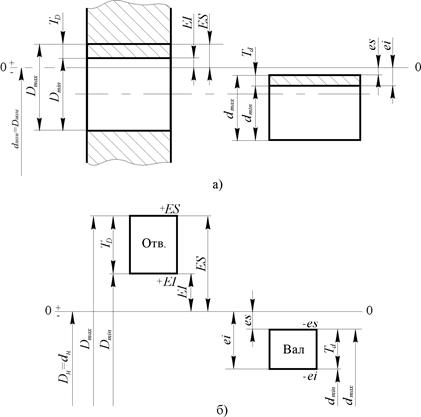
Отклонение — это алгебраическая разность между размером (действительным, предельным и т.д.) и соответствующим номинальным размером. Отклонения отверстий обозначают Е, валов е. (ГОСТ 25346-89) Отклонения могут быть как положительными, так и отрицательными. Поэтому отклонения всегда указываются со своим знаком. Основным отклонением называется отклонение ближайшее к нулевой линии. Предельное отклонение равно алгебраической разности между предельным и номинальным размером. Различают верхнее и нижнее отклонения. Верхнее отклонение, обозначаемое (ES -отверстие, es -вал) равно алгебраической разности между наибольшими предельным и номинальным размерами ES = Dmax - Dnom es = dmax - dno m Нижнее отклонение (EI, ei) равно алгебраической разности между наименьшим предельным и номинальным размерами. EI = Dmin - Dnom ei = dmin - dnom Предельные отклонения позволяют на чертежах указать положение поля допуска относительно номинального размера и определить предельные размеры: Dmax = Dnom + ES dmax = dnom + es Dmin = Dnom + EI dmin = dnom + ei В таблице допусков предельные отклонения приведены в микрометрах, на чертежах отклонения проставляются в миллиметрах. Разброс действительных размеров деталей неизбежен, но при этом действительные размеры годных деталей должны находиться в допустимых пределах, которые в каждом случае определяются значениями предельных размеров. Отсюда и происходит такое понятие как допуск размера. Допуск размера — это разность между наибольшим и наименьшим предельными размерами или алгебраическая разность между верхним и нижним отклонениями (ГОСТ 25346-89). Допуск — величина всегда положительная. Это вытекает из определения допуска. Наиболее часто допуск обозначается: TD — допуск отверстия, Td — допуск вала. Встречаются обозначения — t, IT. Допуск характеризует требуемую точность изготовления размера. TD = Dmax - Dmin = ES – EI Td = dmax - d min = es - ei Поле допуска определяет не только значение относительно номинального размера, но и расположение его пределов, т.е. указывает на предельные размеры. Поле допуска может быть задано численно – предельными отклонениями - ES, EI или es, ei; предельными размерам Dmax, Dmin; или dmax, dmin. или графически. Поле допуска схематично представляют в виде прямоугольника, расположенного по отношению к нулевой линии так, что его верхняя сторона определяет верхнее предельное отношение, а нижняя — нижнее. Графически высота прямоугольника изображает значение допуска. Длина прямоугольника произвольна. При графическом изображении допусков и посадокотклонения размеров откладываются от нулевой линии — линии, соответствующей номиналу размеров. Положительное отклонение откладывается вверх от нулевой линии, отрицательное — вниз. Графический способ изображения допусков и отклонений нагляден, позволяет быстро определить характер соединения деталей, облегчает выполнение расчета посадки. На рис.2. приведены: эскизное изображение деталей (а) и графическое изображение полей допусков (б) с указанием предельных размеров и отклонений.
Рисунок 2.Эскизное изображение деталей (а) и графическое изображение полей допусков (б) с указанием предельных размеров и отклонений.
Посадка — это характеристика сопряжения поверхностей деталей, определяемая значениями получающихся в нем зазоров или натягов. Посадки образуются сочетанием поля допуска отверстия и поля допуска вала. Условное обозначение посадки дается в виде дроби, причем в числителе указывают обозначение поля допуска отверстия, а в знаменателе — обозначение поля допуска вала. Стандарт предусматривает следующие записи посадки: в виде дроби с горизонтальной чертой Посадки могут быть образованы сочетанием любых полей допусков отверстия и вала одного или разных квалитетов. Однако, в первую очередь, должны выбираться посадки предпочтительного применения. При этом соединения деталей (отверстий и валов) традиционно основываются на применении основных отверстий Н и основных валов h.. Посадки, в зависимости от взаимного расположения полей допусков (действительных размеров) отверстия и вала делятся на посадки с зазором, натягом и переходные. Зазор – просвет между валом и отверстием в сопряжении, где размер отверстия больше размера вала. Численно он равен разности реальных размеров отверстия и вала. Натяг – это суммарная упругая деформация отверстия и вала в сопряжении, когда реальный размер вала до сборки больше размера отверстия в сопряжении. Численно он равен разности реальных размеров вала и отверстия перед соединением (сборкой). В сборе их размеры одинаковы. При условии двух или более посадок на одном номинальном размере детали возможны две системы образования посадок - система отверстия и система вала. В системе отверстия — предельные отклонения отверстий одинаковы (при неизменном номинальном размере и заданной точности), а различные посадки достигаются путем назначения различных предельных размеров валов. В системе вала — предельные отклонения валов одинаковы (при неизменном номинальном размере и заданной точности), а различные посадки достигаются путем назначения различных предельных размеров отверстий. Система отверстия для большинства случаев является предпочтительной, как более экономичная. Различные по размерам валы в системе отверстия обрабатываются одним и тем же резцом или шлифовальным кругом, следовательно, небольшим типоразмером необходимого инструмента. Для получения разнообразных посадок в системе вала требуется изменять размеры отверстий, что требует увеличения типоразмеров режущего инструмента. Выбор посадок, или точнее, значений наименьших и наибольших зазоров и натягов (основных характеристик посадок) или значение допусков сопрягаемых деталей предопределяет качество выполнения соединением своего функционального назначения и стоимость изготовления деталей (точнее квалитет — больше стоимость обработки). Посадкой с зазором называется посадка, при которой гарантируется зазор в соединении. Это возможно только тогда, когда размеры отверстия больше размера вала. На схеме поле допуска отверстия расположено всегда над полем допуска вала. Предельные зазоры определяются исходя из служебного назначения. Действительные значения получающихся зазоров должны находиться между двумя предельными значениями зазоров, которые чертежами непосредственно не устанавливаются. Посадкой с натягом называется посадка, при которой обеспечивается натяг в соединении. Это возможно только тогда, когда размер вала больше размера отверстия. На схеме поле допуска вала всегда расположено над полем допуска отверстия. Предельные натяги определяются исходя из служебного назначения. Действительные значения получающихся натягов должны находиться между двумя предельными значениями натягов, которые чертежами непосредственно не устанавливаются. Переходной посадкой называется посадка, при которой возможно, для конкретного сопряжения, получение либо зазора, либо натяга. В такой посадке поля допусков отверстия и вала полностью или частично перекрывают друг друга Пример расчёта посадки с зазором
Задача: выбрать посадку распорной втулки на вал диаметром 32 мм, провести вероятностный расчет посадки. Основным назначением распорной втулки является фиксация размера между подшипником качения и зубчатым колесом. Особых требований по точности сопряжения предъявлять нет надобности, соединение должно собираться легко, поэтому назначаем посадку для данного соединения Ø32Н9/d9. Рассчитываем предельные размеры отверстия Ø32Н9. По ГОСТ 25346-89 «Основные нормы взаимозаменяемости. Единая система допусков и посадок. Общие положения, ряды допусков и основных отклонений» определяем значения допуска IT9 = 62 мкм и основного (нижнего) отклонения EI = 0 мкм. Верхнее отклонение будет равно
ES = EI + IT9 = 0 + 62 = +62 мкм. Предельные размеры отверстия:
Dmin = D0 + EI = 32,000 + 0 = 32,000 мм; Dmax =D0 + ES = 32,000 +0,062 = 32,062 мм.
Рассчитываем предельные размеры вала Ø32d9. По ГОСТ 25346 определяем значения допуска IT9 = 62 мкм и основного (верхнего) отклонения es = -80 мкм. Нижнее отклонение будет равно
ei = es – IT9 = – 80 – 62 = – 142 мкм. Предельные размеры вала:
dmin = d0 + ei = 32,000 – 0,142 = 31,858 мм; dmax = d0 + es = 32,000 – 0,080 = 31,920 мм. Результаты расчётов оформим в виде таблицы.
Таблица 1 Расчёт предельных размеров сопряжения
Строим схему расположения полей допусков сопрягаемых деталей и рассчитываем предельные значения зазоров.
Рис.3. Схема расположения полей допусков вала и втулки
Smax = Dmax – dmin = 32,062 – 31,858 = 0,204 мм; Smin = Dmin – dmax = 32,000 – 31,920 = 0,080 мм.
Средний зазор
Scp = (Smax + Smin)/2 = (0,204 + 0,080)/2 = 0,142 мм.
Допуск посадки
TS = ITD + ITd = 0,062 + 0,062 = 0,124 мм. Принимаем, что и размеры вала, и размеры распорной втулки распределены по нормальному закону, и центр группирования каждого из размеров совпадает с координатой середины поля допуска. При нормальном распределении параметра 99,73% всех значений попадают в диапазон, ограниченный значением 6 стандартных отклонений (± 3σ). Если мы примем, что данный диапазон равен допуску (Т = 6σ), то на долю несоответствующих единиц продукции будет приходиться 0,27% деталей, что для условий машиностроительного производства является приемлемым. Следовательно, стандартное отклонение значений нормируемого параметра можно рассчитать по приближенной формуле как шестую часть допуска:
s d = Т d /6, s D = Т D /6. Тогда стандартное отклонение посадки получим путем геометрического суммирования стандартных отклонений размеров вала и втулки:
Так как зазор – разность между диаметрами втулки и вала, то при распределении размеров в партии деталей по нормальному закону сами зазоры также будут распределены по нормальному закону. Центр группирования зазоров будет соответствовать среднему значению зазора. Таким образом, предельные значения вероятных зазоров можно получить как
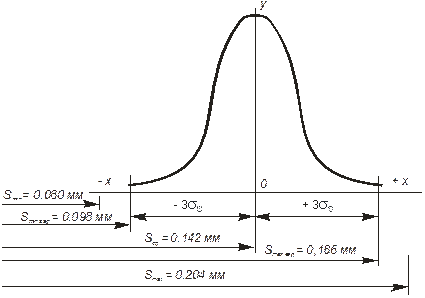
Smax.вер.= Scp + 3sS; Smin.вер.= Scp – 3sS. Рассчитаем предельные значения вероятных зазоров.
Рис.4. Схема распределения вероятных зазоров сопрягаемых деталей Smax.вер. = 142 + 3×14,6 = 185,8 мкм» 0,186 мм; Smin.вер. = 142 – 3×14,6 = 98,2 мкм» 0,098 мм.
Пример расчёта переходной посадки
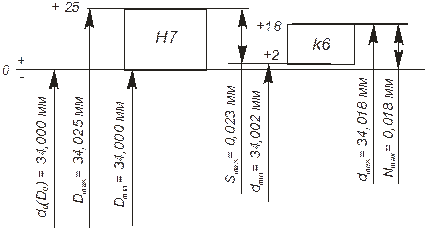
Задание: выбрать посадку зубчатого колеса на вал диаметром 34 мм, провести вероятностный расчет посадки. Выбор посадки зубчатого колеса на вал определяются условиями работы передачи, точностью передачи, условиями сборки узла. Для колёс, перемещаемых вдоль оси вала, применяют посадки Н7/g6; H7/h6, для неподвижных колёс – H7/js7; H7/k6. При значительных скоростях и динамических нагрузках рекомендуются посадки H7/n6; Н7/р6; H7/s6. Для тихоходных колёс невысокой точности (9...10 степени точности) применяют посадки H8/h7; H8/h8. В данном примере выбираем переходную посадку Ø34H7/k6, которая позволит обеспечить точность центрирования сопрягаемых деталей, возможность самоустановки колеса под нагрузкой, легкость сборки и разборки соединения. Рассчитываем предельные размеры отверстия Ø34Н7. По ГОСТ 25346 определяем значения допуска IT7 = 25 мкм и основного (нижнего) отклонения EI = 0 мкм. Верхнее отклонение будет равно
ES = EI + IT9 = 0 + 25 = +25 мкм. Предельные размеры отверстия: Dmin = D0 + EI = 34,000 + 0 = 34,000 мм; Dmax = D0 + ES = 34,000 +0,025 = 34,025 мм. Рассчитываем предельные размеры вала Ø34k6. По ГОСТ 25346 определяем значения допуска IT6 = 16 мкм и основного (нижнего) отклонения ei = +2 мкм. Верхнее отклонение будет равно
es = ei + IT6 = +2 + 16 = +18 мкм. Предельные размеры вала:
dmin = d0 + ei = 34,000 + 0,002 = 34,002 мм; dmax = d0 + es = 34,000 + 0,018 = 34,018 мм.
Результаты расчётов оформим в виде таблицы.
Таблица 2 Расчёт предельных размеров деталей сопряжения
Строим схему расположения полей допусков сопрягаемых деталей и рассчитываем предельные значения табличных зазоров (натягов).
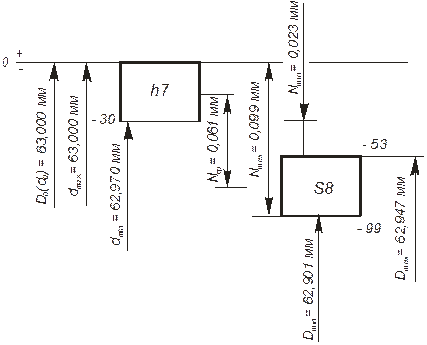
Dcp = (Dmax + Dmin)/2 = (34,025 + 34,000)/2 = 34,0125 мм; dcp = (dmax + dmin)/2 = (34,002 + 34,018)/2 = 34,010 мм; Smax = Dmax – dmin = 34,025 – 34,002 = 0,023 мм; Nmax = dmax – Dmin = 34,018 – 34,000 = 0,018 мм;
Допуск посадки
T(S,N) = ITD + ITd = 0,025 + 0,016 = 0,041 мм. Принимаем нормальный закон распределения размеров и рассчитываем предельные значения вероятных зазоров (натягов). В рассматриваемом сопряжении
Dcp > dcp,
поэтому в данном сопряжении будет большая вероятность возникновения зазоров. Рассчитываем математическое ожидание и стандартное отклонение зазоров:
MS = Dcp – dcp = 34,0125 – 34,010 = 0,0025 мм; Примечание. Если средний диаметр отверстия меньше среднего диаметра вала, то в сопряжении будет большая вероятность возникновения натягов. В этом случае рассчитывают математическое ожидание натягов. Если средний диаметр отверстия равен среднему диаметру вала, то в сопряжении будет одинакова вероятность возникновения зазоров и натягов. Математическое ожидание зазоров и натягов в этом случае равно нулю.
Рассчитаем предельные значения вероятных зазоров и натягов:
Smax.вер. = MS + 3s(S,N) = 2,5 + 3×4,9 = 17,2 мкм = 0,017 мм; Smin.вер. = MS – 3s(S,N) = 2,5 – 3×4,9 = –12,2 мкм; Nmax.вер = 12,2 мкм = 0,012 мм.
Рис.5. Схема расположения полей допусков сопрягаемых деталей
При применении переходных посадок в сопряжениях возможны зазоры или натяги. Поэтому рассчитываем вероятность их получения. Для определения площади, заключённой между кривой Гаусса, выбранными ординатами и осью абсцисс (на рис.5 заштрихована площадь, определяющая процент зазоров), удобно использовать табулированные значения функции (приложение 3).
где
В данном примере
х = MS = 2,5 мкм; s(S,N) = 4,9 мкм. Тогда
z = MS/ s(S,N) = 2,5/4,9 = 0,51; Ф(z=0,51) = 0,1950 = 19,5 % Таким образом, с учетом симметрии распределения (P" = = 0,5), вероятность получения зазоров в сопряжении Æ34Н7/k6 составляет
Р(S) = 50 % + 19,5 % = 69,5 %.
Определим вероятность получения натягов, принимая что 0,9973 ≈ 1
Р(N) = 30,5%.
Рис.6. Распределение вероятных зазоров (натягов) Пример расчёта посадки с натягом
В рассматриваемом узле редуктора применение посадки с натягом нецелесообразно. Поэтому в методическом плане приводим пример расчёта посадки с натягом, который может быть использован в другом узле или как вариант задания контрольной работы. Принимаем сопряжение Æ63S8/h7.
Таблица 3 Расчёт предельных размеров сопряжения
Строим схему расположения полей допусков сопрягаемых деталей и рассчитываем предельные значения табличных натягов.
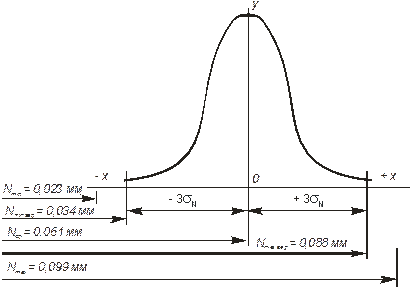
Nmax = dmax – Dmin = 63,000 – 62,901 = 0,099 мм; Nmin = dmin – Dmax = 62,970 – 62,947 = 0,023 мм; Ncp = (Nmax + Nmin)/2 = (0,099 + 0,023)/2 = 0,061 мм.
Допуск посадки
TN = ITD + ITd = 0,046 + 0,030 = 0,076 мм. Принимаем нормальные законы распределения случайных размеров и рассчитываем предельные значения вероятных натягов:
Рис.7. Схема расположения полей допусков сопрягаемых деталей
Nmax.вер.= Ncp + 3sN;
Nmin.вер.= Ncp – 3sN; где sN – стандартное отклонение сопряжения.
Nmax.вер. = 61 + 3×9,1 = 88,3 мкм» 0,088 мм; Nmin.вер. = 61 – 3×9,1 = 33,7 мкм» 0,034 мм.
Рис.8. Распределение вероятных натягов
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 209; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.2.242 (0.009 с.) |

 ; с косой чертой — H7 / g6, поля допусков отверстия и вала разделяются тире — H7 - g6.
; с косой чертой — H7 / g6, поля допусков отверстия и вала разделяются тире — H7 - g6.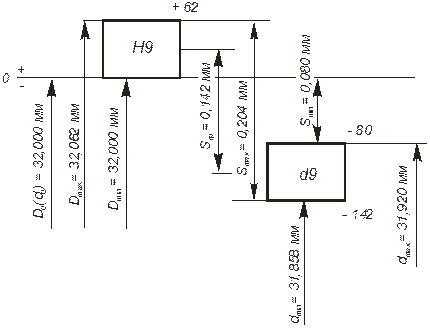
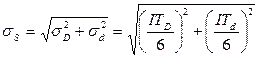 .
.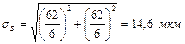 ;
; 
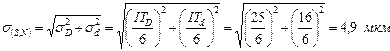 .
.
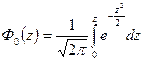 ,
,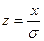 .
.
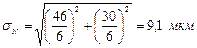 ;
;