
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
С помощью каких команд строятся графики на плоскости и в пространстве. Какие аргументы имеют эти команды.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
· plot(f(x), x=a..b, y=c..d, parameters), (parameters – параметры управления изображением) используется для построения графиков функции f(x) одной переменной. · implicitplot(F(x,y)=0, x=x1..x2, y=y1..y2) из графического пакета plots используется для построения графика неявной функции. · inequals({f1(x,y)>c1,…,fn(x,y)>cn}, x=x1…x2, y=y1..y2, options) из пакета plots используется для построения двумерной области. В команде в фигурных скобках указывается система неравенств, определяющих область, затем размеры координатных осей и параметры. · plot3d(f(x,y), x=x1…x2, y=y1…y2, options) используя для построения графика поверхности, заданной неявной функции · plot3d([x(u,v), y(u,v), z(u,v)], u=u1..u2, v=v1..v2) используя для построения поверхности, заданной параметрически (функции перечисляются в квадратных скобках в команде). · implicitplot3d(F(x,y,z)=c, x=x1..x2, y=y1..y2, z=z1..z2) из пакета plot используя для построения трехмерного графика поверхности, заданной неявно уравнением · spacecurve из пакета plot используя для построения пространственной кривой, заданной параметрически:
Как называется пакет дополнительных графических команд? Пакет дополнительных графических команд называется plots
С помощью какой команды можно построить график неявной функции? Для построения графика неявной функции используется команда implicitplot из графического пакета plots: implicitplot(F(x,y)=0, x=x1..x2, y=y1..y2).
Для чего предназначена команда display? Команда display предназначена для вывода графических изображений на экран.
Какая команда позволяет построить двумерную область, заданную системой неравенств? Если необходимо построить двумерную область, заданную системой неравенств
С помощью какой команды можно построить график пространственной кривой? В пакете plot имеется команда spacecurve для построения пространственной кривой.
Какие возможности предоставляют команды animate и animate3d? Команды animate (двумерные) и animate3d (трехмерные) из пакета plot позволяют выводить на экран движущиеся изображения. Среди параметров команды animate3d есть frames – число кадров анимации (по умолчанию frames=8).
Лабораторная работа №4 Математический анализ: дифференциальное исчисление функции одной и многих переменных. Контрольные задания. 1. Вычислите предел > restart; > Limit(((x^2-2*x+1)/(x^2-4*x+2))^x,x=infinity)=limit(((x^2-2*x+1)/(x^2-4*x+2))^x,x=infinity);
2. Найти пределы функции > Limit(1/(1+2^(1/x)),x=0,left)=limit(1/(1+2^(1/x)),x=0,left); Ответ: > Limit(1/(1+2^(1/x)),x=0,right)=limit(1/(1+2^(1/x)),x=0,right); Ответ: 3. Найти > restart; > Diff(ln(x),x$5)=diff(ln(x),x$5): > collect(%,exp(x)); Ответ:
4. Найти все частные производные 2 – ого порядка функции
> restart; > f:=arctan((x+y)/(1-x*y)): > Diff(f,x$2)=simplify(diff(f,x$2));
> Diff(f,y$2)=simplify(diff(f,y$2));
> Diff(f,x,y)=diff(f,x,y);
> simplify(%);
Ответ:
5. Найти точки разрыва функции > restart; > readlib(singular): > iscont((1/(1-exp(x/(1-x)))),x=-infinity..infinity);
> discont(1/(1-exp^(x/(1-x))),x); Ответ: 6. Найти экстремумы функции > restart; > f(x):=x*sin(x)+cos(x)-(x^2/4);
> extrema(f(x),{},x,'s');s; Ответ:
> maximize(f(x),x=-1..1); Ответ: > minimize(f(x),x=-1..1); Ответ: Лабораторная работа №5 Математический анализ: интегральное исчисление функции одной и многих переменных. Преобразование Лапласа. Контрольные задания 1. Вычислить неопределенный интеграл
> restart; > Int((x^3-6)/(x^4+6*x^2+8),x)= int((x^3-6)/(x^4+6*x^2+8),x);
Ответ:
2. Вычислить несобственный интеграл
> restart; > assume(a>0):assume(b>0): > additionally(a>b):Int(sin(a*x)*cos(b*x)/x,x=0..+infinity)=int(sin(a*x)*cos(b*x)/x,x=0..+infinity); Ответ: > restart; > assume(a>0):assume(b>0): > f:=sin(a*x)*cos(b*x)/x: > additionally(a=b):Int(sin(a*x)*cos(b*x)/x,x=0..+infinity)=int(sin(a*x)*cos(b*x)/x,x=0..+infinity); Ответ: > restart; > assume(a>0):assume(b>0): > f:=sin(a*x)*cos(b*x)/x: > additionally(a<b):Int(sin(a*x)*cos(b*x)/x,x=0..+infinity)=int(sin(a*x)*cos(b*x)/x,x=0..+infinity); Ответ:
3. Численно найти интеграл
> restart; > Int(sin(3*x)*exp(-1*x^2)/x^4, x=0.1..0.2)= evalf(int(sin(3*x)*exp(-1*x^2)/x^4, x=0.1..0.2));
Ответ:
4. Полностью проделать все этапы вычисления интеграла > restart; > f:=x^3*cos(x);
> with(student):J:=Int(f,x=0..Pi/2);
> J:=intparts(Int(f,x=0..Pi/2),x^3);
> intparts(%,x^2);
> intparts(%,x);
> value(%);
Ответ:
5. Вычислить интеграл
> restart; > with(student): > J=Int(1/(5-4*sin(x)+3*cos(x)), x=0..Pi/2);
> J=changevar(tan(x/2)=t,Int(1/(5-4*sin(x)+3*cos(x)), x=0..Pi/2),t);
> value(%); Ответ:
6. Вычислить тройной интеграл:
> restart: with(student): > J:=Tripleint(ln(z-x-y)/((x-exp)*(x+y-exp)),x=exp..x+y+exp, y=0..exp-x-1, z=0..exp-1);
> value(%);
Ответ:
7.Найти изображения Лапласа и построить их графики для следующих функций: а) > restart; > with(inttrans): > F(p):=laplace(sin(t)/t,t,p); Ответ: > plot(F(p),p);
> restart; > with(inttrans): > F(p):=laplace(((1-cos(2*t))*exp(-3*t))/t,t,p); Ответ: > plot(F(p),p);
8. Найти оригинал Лапласа функции
> restart; > with(inttrans): > F(x):=invlaplace(1/(((p-1)^2)*(p^2+1)),p,x): > combine(%,trig);
Ответ: > plot(F(x),x);
9.Дана функция
> restart; > f(x):=int((1-cos(x*t))/x^2,x=0..+infinity);
> with(inttrans): > F(p):=laplace(f(x),t,p);
> plot(F(p),p);
Контрольные вопросы. 1. Что такое команды прямого и отложенного исполнения? Опишите их действия. Ø Прямого исполнения – int(f, x), где f – подынтегральная функция, x – переменная интегрирования – вычисляет интеграл; Ø Отложенного исполнения – Int(f, x) – где параметры команды такие же, как и в команде прямого исполнения int – выдает на экран интеграл в аналитическом виде математической формулы. 2. Какие команды производят аналитическое и численное интегрирование? Опишите их параметры. int(f, x), где f – подынтегральная функция, x – переменная интегрирования (для вычисления определенного интеграла добавляются пределы интегрирования) Если в команде интегрирования добавить опцию continuous: int(f, x, continuous), то Maple будет игнорировать любые возможные разрывы подынтегральной функции в диапазоне интегрирования. Численное интегрирование выполняется командой evalf(int(f, x=x1..x2), e), где e – точность вычислений (число знаков после запятой). 3. С помощью каких команд вводятся ограничения на параметры для вычисления интегралов, зависящих от параметров? Ограничения на параметры вводятся при помощи команды assume(expr1), где expr1 – неравенство. Дополнительные ограничения вводятся с помощью команды additionally(expr2), где expr2 – другое неравенство, ограничивающее значение параметра с другой стороны. 4. Для чего предназначен пакет student? Пакет student, предназначенный для обучения математике. Он содержит набор подпрограмм, предназначенных для выполнения расчетов шаг за шагом, так, чтобы была понятна последовательность действий, приводящих к результату. 5. Опишите команду интегрирования по частям. Если обозначить подынтегральную функцию f=u (x) v’ (x), то параметры команды интегрирования по частям такие: intparts(Int(f, x), u), где u – именно та функция u(x), производную от которой предстоит вычислить по формуле интегрирования по частям. Эта команда не вычисляет окончательно интеграл, а лишь производят промежуточную выкладку. Для того, чтобы получить окончательный ответ, следует, после выполнения этой команды ввести команду value(%); где % - обозначают предыдущую строку. 6. Опишите команду интегрирования методом замены переменных. Если в интеграле требуется сделать замену переменных x=g (t) или t=h (x), то параметры команды замены переменных такие: changevar(h(x)=t, Int(f, x), t), где t - новая переменная. Эта команда, так же как и intparts не вычисляют окончательно интеграл, а лишь производят промежуточную выкладку. 7. Какие команды используются для вычисления двойных и тройных интегралов? Опишите их параметры. В Maple имеются две специальные команды для вычисления двойных и тройных интегралов, содержащиеся в библиотеке student.
Для вычисления двойных интегралов используется команда Doubleint(f(x, y), D), где D – область интегрирования, записываемая в одном из следующих форматов: § x=х1..х2, y=y1..y2, где числа х1, х2, y1, y2 задают прямоугольную область интегрирования; § x=f1(y)..f2(y), y=y1..y2, где f1(y), f2(y) - линии, ограничивающие область интегрирования слева и справа на интервале от y1 до y2; § x=х1..х2, y=g1(x)..g2(x), где g1(y), g2(y) - линии, ограничивающие область интегрирования снизу и сверху на интервале от х1 до х2. Для вычисления тройных интегралов используется команда Tripleint(f(x, y, z),x, y, z, V), где V – область интегрирования. Обе эти команды являются командами отложенного действия. Чтобы получить значение интеграла, следует использовать команду value(%). Лабораторная работа №6 " Дифференциальные уравнения. Ряды" Контрольные задания 1.Найти сумму ряда > restart; > Sum(1/(n*(n+1)*(n+2)), n=1..infinity)=sum(1/(n*(n+1)*(n+2)), n=1..infinity);
> S[N]:=Sum(1/(n*(n+1)*(n+2)),n=1..N)=sum(1/(n*(n+1)*(n+2)),n=1..N);
> s:=limit(rhs(S[N]), N=+infinity);
Ответ:
2.Разложить в степенной ряд f (x)=arcsin x в окрестности x =0 до 9-ого порядка.
> restart; > f(x)=series((arcsin(x)), x=0, 9);
Ответ: 3.Разложить в ряд Тейлора функцию > restart; > readlib(mtaylor): > f=mtaylor(arctan((x-y)/(1+x*y)),[x=0,y=0], 7);
> f = x-y-1/3*x^3+1/3*y^3+1/5*x^5-1/5*y^5;
Ответ: 4.Разложить в ряд Фурье функцию > restart; > fourierseries:=proc(f,x,x1,x2,n) local k, l, a, b, s; > l:=(x2-x1)/2; > a[0]:=int(f,x=x1..x2)/l; > a[k]:=int(f*cos(k*Pi*x/l),x=x1..x2)/l; > b[k]:=int(f*sin(k*Pi*x/l),x=x1..x2)/l; > s:=a[0]/2+sum(a[k]*cos(k*Pi*x/l)+ b[k]*sin(k*Pi*x/l), k=1..n);
> end;
> f:=piecewise(0<x and x<2, 6, 2<=x and x<4, 3*x);
> x1:=0:x2:=4: > fr:=fourierseries(f,x,x1,x2,6);
> plot({fr,f}, x=x1..x2, color=[blue,black],thickness=2, linestyle=[3,1]);
5. Найти общее решение дифференциального уравнения:
> restart; > deq:=diff(y(x),x$2)-2*diff(y(x),x)-3*y(x)=x*exp(4*x)*sin(x);
> dsolve(deq,y(x));
6. Найти фундаментальную систему решений дифференциального уравнения:
> restart; > de:=diff(y(x),x$3)+diff(y(x),x$2)=1-6*x^2*exp(-x);
> dsolve(de, y(x), output=basis);
Ответ: 7. Найти решение задачи Коши: y² –3y ¢+2y= y(0)=1+8ln2,y¢ (0)=14ln2,
> restart; > de:= diff(y(x),`$`(x,2))-3*diff(y(x),x)+2*y(x) = 1/(3+exp(-x));
> cond:=y(0)=1+8*ln(2), D(y)(0)=14*ln(2);
> dsolve({de,cond},y(x));
Ответ:
8. Найти решение системы дифференциальных уравнений:
при начальных условиях х (0)=1, х '(0)=0; у (0)=1. > restart; > sys:=diff(x(t),t$2)+5*diff(x(t),t)+2*diff(y(t),t)+y(t)=0,3*diff(x(t),t$2)+5*x(t)+diff(y(t),t)+3*y(t)=0: > dsolve({sys},{x(t),y(t)});
> cond:=x(0)=1, D(x)(0)=0, y(0)=1;
> dsolve({sys,cond},{x(t),y(t)});
Ответ: 9. Найти решение нелинейного уравнения
> restart; > Order:=6: > dsolve({diff(y(x),x$2)+y(x)=(y(x))^2,y(0)=2*a,D(y)(0)=a},y(x),type=series);
Ответ:
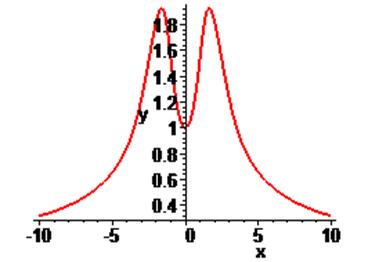
10. Построить график численного решения задачи Коши у '=sin(xy), у (0)=1.
> restart; > Ordev=6: > eq:=diff(y(x),x)=sin(x*y(x)): > cond:=y(0)=1: > de:=dsolve({eq,cond},y(x),numeric);
> de(0);
> with(plots): > odeplot(de,[x,y(x)],-10..10,thickness=2);
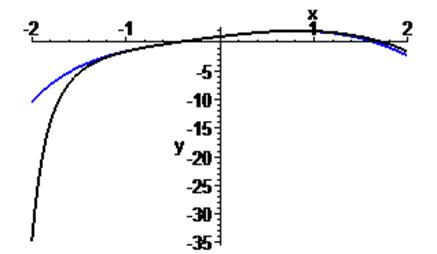
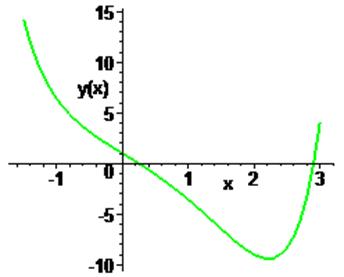
11. Решить численно задачу Коши: > restart; > Ordev=6: > eq:=diff(y(x),x$2)=x*diff(y(x),x)-(y(x))^2: > cond:=y(0)=1, D(y)(0)=2: > de:=dsolve({eq,cond},y(x),numeric);
> de(0.5);
> dsolve({eq, cond}, y(x), series);
> convert(%, polynom):p:=rhs(%): > with(plots): > p1:=odeplot(de,[x,y(x)],-2..2, thickness=2,color=black): > p2:=plot(p,x=-2..2,thickness=2,linestyle=3,color=blue): > display(p1,p2);
Ответ:
12. Построить график численного решения задачи Коши у ''- xу '+ xу =0, у (0)=1, у '(0)=-4 на интервале [-1.5; 3], используя команду DEplot
> restart; > with(DEtools): > DEplot(diff(y(x),x$2)-x*diff(y(x),x)+x*y(x)=0,y(x),x=-1.5..3,[[y(0)=1,D(y)(0)=-4]],stepsize=.1,linecolor=green, thickness=2);
Контрольные вопросы 1. Какая команда позволяет решить дифференциальное уравнение? Опишите ее параметры. Для нахождения аналитических решений дифференциальных уравнений в Maple применяется команда dsolve(eq,var,options), где eq – дифференциальное уравнение, var – неизвестные функции, options – параметры. Параметры могут указывать метод решения задачи, например, по умолчанию ищется аналитическое решение: type=exact. При составлении дифференциальных уравнений для обозначения производной применяется команда diff. 2. С помощью каких операторов обозначается производная в дифференциальном уравнении и в начальных условиях? При составлении дифференциальных уравнений для обозначения производной применяется команда diff. Для обозначения производных в начальных или краевых условиях используется дифференциальный оператор 3. Какой параметр команды dsolve следует установить, чтобы получить фундаментальную систему дифференциальных уравнений? Команда dsolve предоставляет возможность найти фундаментальную систему решений дифференциального уравнения. Для этого в параметрах команды dsolve следует указать output=basis. 4. Какой параметр команды dsolve следует установить, чтобы получить приближенное решение дифференциального уравнения в виде разложения в степенной ряд? Как определяется порядок разложения? Чтобы найти приближенное решение дифференциального уравнения в виде степенного ряда, в команде dsolve следует после переменных указать параметр type=series (или просто series). Для того, чтобы указать порядок разложения n, т.е. порядок степени, до которой производить разложение, следует перед командой dsolve вставить определение порядка с помощью команды Order:=n. 5. Опишите, какие команды нужно ввести, прежде чем построить график приближенного решения, полученного в виде степенного ряда. Разложение в степенной ряд имеет тип series, поэтому для дальнейшей работы с этим рядом его следует преобразовать в полином с помощью команды convert(%,polynom), а затем выделить правую часть полученного выражения командой rhs(%).
6. Какой параметр команды dsolve следует установить, чтобы решить дифференциальное уравнение численно? Для того, чтобы найти численное решение дифференциального уравнения (задачи Коши или краевой задачи) в команде dsolve следует указать параметр type=numeric (или просто numeric). 7. Как найти значение решения дифференциального уравнения в какой-либо конкретной точке? Если необходимо получить значение решения при каком-то фиксированном значении переменной х (заодно будет выведено значение производной решения в этой точке), например, при х =0.5, то следует набрать: > de(0.5); 8. Какая команда позволяет построить график численно решенного дифференциального уравнения? График численного решения дифференциального уравнения можно построить с помощью команды odeplot(dd, [x,y(x)], x=x1..x2), где в качестве функции используется команда dd:=dsolve({eq,cond}, y(x), numeric) численного решения, после нее в квадратных скобках указывают переменную и неизвестную функцию [x,y(x)], и интервал x=x1..x2 для построения графика. Команда odeplot находится в специальном пакете DEtools. 9. Какой пакет предназначен для графического представления и численного решения дифференциального уравнения? Для численного решения задачи Коши, построения графиков решения и фазовых портретов в Maple имеется специальный пакет DEtools. 10. В чем отличие команд odeplot и DEplot? Команда DEplot из пакета DEtools аналогична команде odeplot, но более функциональна. Она, в отличие от odeplot, сама производит численное решение дифференциального уравнения. 11. Как вычислить сумму или произведение в Maple?
Конечные и бесконечные суммы вычисляются командой прямого исполнения sum и отложенного исполнения Sum. Аргументы этих команд одинаковые: sum(expr, n=a..b), где expr – выражение, зависящее от индекса суммирования, a..b – пределы индекса суммирования, указывающие, что суммировать следует от n=a до n=b. Если требуется вычислить сумму бесконечного ряда, то в качестве верхнего предела вводится infinity.
|
|||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 1199; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.167.15 (0.014 с.) |

 .
. , где указывается уравнение поверхности
, где указывается уравнение поверхности 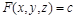 и размеры рисунка по координатным осям.
и размеры рисунка по координатным осям.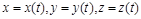 .
. , то для этого можно использовать команду inequal из пакета plots. В команде inequals({f1(x,y)>c1,…,fn(x,y)>cn}, x=x1…x2, y=y1..y2, options) в фигурных скобках указывается система неравенств, определяющих область, затем размеры координатных осей и параметры.
, то для этого можно использовать команду inequal из пакета plots. В команде inequals({f1(x,y)>c1,…,fn(x,y)>cn}, x=x1…x2, y=y1..y2, options) в фигурных скобках указывается система неравенств, определяющих область, затем размеры координатных осей и параметры. .
. Ответ:
Ответ: при
при  и при
и при  .
.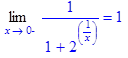

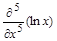 .
.
 .
.

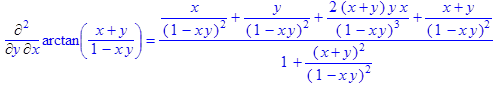


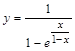 .
.

 ,
,  и указать их характер.
и указать их характер.




 .
.
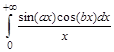 при a >0 b >0 для случаев a > b, a = b, a < b.
при a >0 b >0 для случаев a > b, a = b, a < b.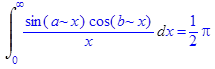
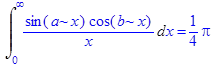

 .
.
 по частям
по частям
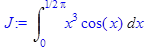

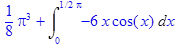
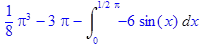
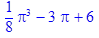
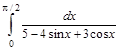
 с помощью универсальной подстановки tg(x /2)= t.
с помощью универсальной подстановки tg(x /2)= t.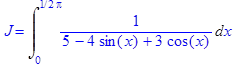

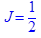
 .
.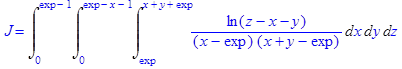
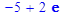
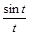 ; б)
; б) 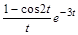 .
.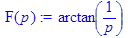

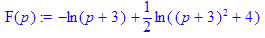

 и построить его график.
и построить его график.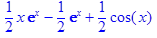
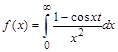 , найти ее изображение Лапласа.
, найти ее изображение Лапласа.
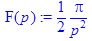
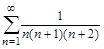 и сумму первых N членов.
и сумму первых N членов.
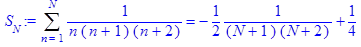

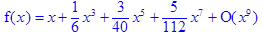
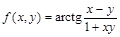 до 6 – ого прядка в окрестности точки (0, 0).
до 6 – ого прядка в окрестности точки (0, 0).
 с периодом 4 на интервале [0;4], удерживая 6 членов ряда. Построить на одном рисунке графики функции и ее n -частичной суммы ряда Фурье.
с периодом 4 на интервале [0;4], удерживая 6 членов ряда. Построить на одном рисунке графики функции и ее n -частичной суммы ряда Фурье.
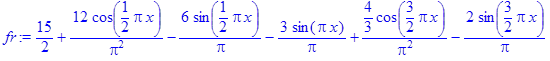


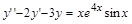

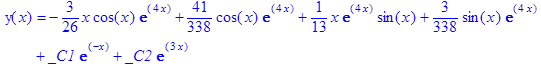
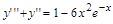
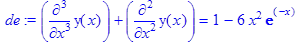
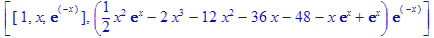
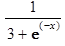
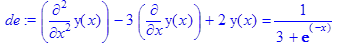
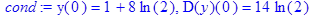
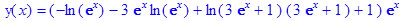
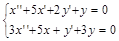
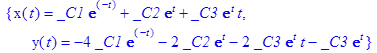
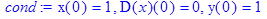

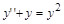 при начальных условиях у (0)=2 а, у '(0)= а в виде разложения в степенной ряд до 6-го порядка.
при начальных условиях у (0)=2 а, у '(0)= а в виде разложения в степенной ряд до 6-го порядка.
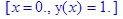
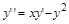 ,
, 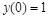 ,
, 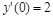 . Найти приближенное решение этого уравнения в виде разложения в степенной ряд. Построить на одном рисунке графики полученных решений.
. Найти приближенное решение этого уравнения в виде разложения в степенной ряд. Построить на одном рисунке графики полученных решений.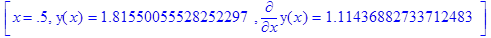
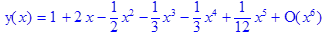
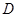 .
.


