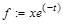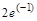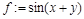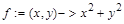Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функции в Maple. Операции оценивания. Решение уравнений и неравенств
Контрольные задания 1. Дано комплексное число > restart; > z:=(2*exp(I*Pi/6))^5: > evalc(Re(z)); evalc(Im(z));
> evalc(readlib(polar)): evalc(polar(z));
2. Записать функцию > restart; > f:=(x,y)->(arctan(x+y)/arctan(x-y))^2;
> f(1,0);
> f((1+sqrt(3))/2,(1-sqrt(3))/2);
3. Записать функцию > restart; > f:=((x^3)*(y^2)-(x^2)*(y^3))/(x*y)^5;
> subs({x=a,y=1/a},f);
4. Найти все точные решения системы > restart; > s:=solve({x^2-5*x*y+6*y^2=0,x^2+y^2=10},{x,y});
5. Найти все решения тригонометрического уравнения > restart; > _EnvAllSolutions:=true: > solve(sin(x)^4-cos(x)^4=1/2, x);
6. Найти численное решение уравнения > restart; > x:=fsolve(exp(x)=2*(1-x)^2, x);
7. Решить неравенство > restart; > s:=solve(2*ln(x)^2-ln(x)<1, x);
Контрольные вопросы. 1. Опишите способы задания функций в Maple. В Maple имеется несколько способов представления функции. Способ 1. Определение функции с помощью оператора присваивания (:=): какому-то выражению присваивается имя, например: > f:=sin(x)+cos(x);
Если задать конкретное значение переменной х, то получится значение функции f для этого х. Например, если продолжить предыдущий пример и вычислить значение f при > x:=Pi/4;
> f;
После выполнения этих команд переменная х имеет заданное значение Чтобы насовсем не присваивать переменной конкретного значения, удобнее использовать команду подстановки subs({x1=a1, x2=a2,…, },f), где в фигурных скобках указываются переменные хi и их новые значения аi (i =1,2,…), которые следует подставить в функцию f. Например: > f:=x*exp(-t);
> subs({x=2,t=1},f);
Способ 2. Определение функции с помощью функционального оператора, который ставит в соответствие набору переменных (x1,x2,…) одно или несколько выражений (f1,f2,…). Например, определение функции двух переменных с помощью функционального оператора выглядит следующим образом: > f:=(x,y)->sin(x+y);
Обращение к этой функции осуществляется наиболее привычным в математике способом, когда в скобках вместо аргументов функции указываются конкретные значения переменных. В продолжение предыдущего примера вычисляется значение функции:
> f(Pi/2,0); Способ 3. С помощью команды unapply(expr,x1,x2,…), где expr – выражение, x1,x2,… – набор переменных, от которых оно зависит, можно преобразовать выражение expr в функциональный оператор. Например: > f:=unapply(x^2+y^2,x,y);
> f(-7,5); Какие операции оценивания производятся в Maple с действительными выражениями? В Maple имеются следующие команды оценивания действительных выражений: frac(expr) - вычисление дробной части выражения expr; trunc(expr) - вычисление целой части выражения expr; round(expr) - округление выражения expr; Для чего предназначена команда evalf? Все вычисления в Maple по умолчанию производятся символьно, то есть результат будет содержать в явном виде иррациональные константы, такие как, и другие. Чтобы получить приближенное значение в виде числа с плавающей запятой, следует использовать команду evalf(expr,t), где expr - выражение, t - точность, выраженная в числах после запятой. С помощью каких команд можно найти вещественную и мнимую части комплексного выражения, а также его модуль и аргумент, и комплексно сопряженное ему число? Какую роль выполняет команда evalc? Вещественную и мнимую части комплексного выражения z=x+iy можно найти с помощью команд Re(z) и Im(z). Например: > z:=3+I*2: > Re(z);Im(z); 3, 2 Если z=x+iy, то комплексно сопряженное ему выражение w=z*=x-iy можно найти с помощью команды conjugate(z). Продолжение предыдущего примера: w:=conjugate(z); w:=3-2 I Модуль и аргумент комплексного выражения z можно найти с помощью команды polar(z), которую необходимо предварительно вызвать из стандартной библиотеки командой readlib. Например: > readlib(polar): polar(I); Если комплексное выражение очень сложное или содержит параметры, то команды Re(z) и Im(z) не дают требуемого результата. Получить вещественную и мнимую части комплексного выражения z можно, если использовать команду преобразования комплексных выражений evalc(z). (> evalc(Re(z)); evalc(Im(z));)
|
|||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 3104; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.131.110.169 (0.014 с.) |
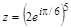 . Найти его вещественную и мнимую части, модуль и аргумент.
. Найти его вещественную и мнимую части, модуль и аргумент.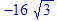
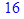
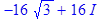
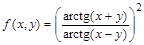 в виде функционального оператора и вычислите ее значения при x =1, y =0 и при
в виде функционального оператора и вычислите ее значения при x =1, y =0 и при 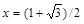 ,
, 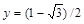 .
.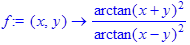
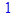
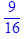
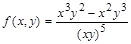 с помощью оператора присваивания и вычислите ее значение при x = a, y =1/ a, используя команду подстановки subs.
с помощью оператора присваивания и вычислите ее значение при x = a, y =1/ a, используя команду подстановки subs.
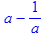
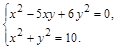 в аналитическом виде.
в аналитическом виде.
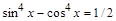 .
.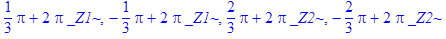
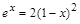 .
.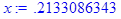
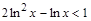 .
.
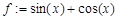
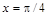 , то следует записать:
, то следует записать: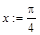
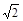
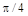 .
.