
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет намагничивающего тока.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
2.5.1. Индукция в зубцах статора Bz1.
2.5.2. Индукция в зубцах ротора Bz2
2.5.3. Индукция в ярме статора Ва:
2.5.4. Расчетная высота ярма ротора h´j. При посадке сердечника непосредственно на вал, в двигателях с 2p=2 и 2p=4, имеем:
2.5.5. Индукция в ярме ротора Вj:
2.5.6. Коэффициент воздушного зазора kδ:
где γ рассчитывается по следующей формуле:
2.5.7. Магнитное напряжение воздушного зазора Fδ:
2.5.8. Значения напряженности поля в зубцах HZ. Находят, в соответствии с индукциями BZ для принятой марки стали. По табл. 37, для стали 2013: - при значении индукции статора BZ1=1,9 Тл значение напряженности поля в зубцах статора HZ1=2070 А/м; - при значении индукции ротора BZ2=1,8 Тл значение напряженности поля в зубцах ротора HZ2=1520 А/м; - расчетная высота зубца статора hz1= hп1; - расчетная высота зубца ротора hz2=hп2-0,1·b2p.
2.5.9. Магнитное напряжение зубцовой зоны статора Fz1 и ротора Fz2:
где hz1 - расчетная высота зубца статора; hz2 - расчетная высота зубца ротора;
2.5.10. Коэффициент насыщения зубцовой зоны kZ:
Полученное значение kZ позволяет предварительно оценить правильность выбранных размерных соотношений и обмоточных данных проектируемой машины. Если kZ>1,5 - 1,6, имеет место чрезмерное насыщение зубцовой зоны; если kZ<1,2, то зубцовая зона мало использована или воздушный зазор взят слишком большим. В обоих случаях в расчет должны быть внесены соответствующие коррективы.
2.5.11. Значения напряженности поля в ярме HZ. Находят, в соответствии с индукциями BZ для принятой марки стали. По табл. 38, для стали 2013: - при значении индукции в ярме статора Ba=1,6 Тл, значение напряженности поля На=750 А/м, - при значении индукции в ярме ротора Вj=0,605 Тл, значение напряженности поля Нj=89 A/м.
2.5.12. Длина средней магнитной линии ярма статора La:
2.5.13. Высота спинки ротора hj:
2.5.14. Длина средней магнитной линии потока в ярме ротора Lj. Для всех двигателей, кроме двухполюсных с непосредственной посадкой на вал:
Для двигателей, с 2р=2, сердечник ротора которых непосредственно насажен на вал, длина средней магнитной линии определяется по формуле: Lj=2·hj. 2.5.15. Магнитное напряжение ярма статора Fa и ярма ротора Fj:
Fa=La·Ha, Fj=Lj·Hj;
2.5.16. Суммарное магнитное напряжение магнитной цепи машины (на пару полюсов): Fц= Fδ+ Fz1+ Fz2+ Fa+ Fj;
2.5.17. Коэффициент насыщения магнитной цепи kμ:
2.5.18. Намагничивающий ток Iμ:
2.5.19. Относительное значение намагничивающего тока I´μ.
Относительное значение I´μ служит определенным критерием правильности проведенного выбора и расчета размеров и обмотки двигателя. Так, если при проектировании четырехполюсного двигателя средней мощности расчет показал, что I´μ<0,2 - 0,18, то это свидетельствует о том, что размеры машины выбраны завышенными и активные материалы недоиспользованы. Если же в аналогичном двигателе I´μ>0,3 - 0,35, то это означает, что либо его габариты взяты меньшими, чем следовало, либо неправильно выбраны размерные соотношения участков магнитопровода. В небольших двигателях мощностью менее 2-3 кВт I´μ может достигать значения 0,5-0,6,несмотря на правильно выбранные размеры и малое насыщение магнитопровода. Это объясняется относительно большим значением магнитного напряжения воздушного зазора, характерным для двигателей малой мощности.
2.6. Параметры рабочего режима. Параметрами асинхронной машины называют активные и индуктивные сопротивления обмоток статора r1, x1, ротора r2, x2, сопротивление взаимной индуктивности x12 и расчетное сопротивление r12, введением которого учитывают влияние потерь в стали статора на характеристики двигателя. Для определения активного сопротивления фазы обмотки статора предварительно необходимо определить: bкт - среднюю ширину катушки, lвыл - длину вылета лобовой части катушки, lп1- длину пазовой части, lл1- длину лобовой части, lср1 - среднюю длину витка, L1 - общую длину проводников фазы обмотки. 2.6.1. Средняя ширина катушки bкт:
где β1 - относительное укорочение шага обмотки статора;
2.6.2. Длина вылета лобовой части катушки lвыл:
где kвыл - коэффициент, значение которого берут из табл. 39 в зависимости от числа полюсов машины и наличия изоляции в лобовых частях. В - длина вылета прямолинейной части катушек из паза от торца сердечника до начала отгиба лобовой части. Для всыпной обмотки, укладываемой в пазы до запрессовки сердечника в корпус, принимаем В=0,01 м.
2.6.3. Длина пазовой части lп1. Равна конструктивной длине сердечников машины: lп1= lcт1.
2.6.4. Длина лобовой части: lл1=kл·bкт+2·В; где kл - коэффициент, значение которого берут из табл. 39 в зависимости от числа полюсов машины и наличия изоляции в лобовых частях. bкт – средняя ширина катушки;
2.6.5. Средняя длина витка lср1: lср1=2·(lп1+ lл1).
2.6.6. Общая длина проводников фазы обмотки L1: L1=lср1·ω1;
Для класса нагревостойкости изоляции F расчетная температура υрасч=1150 С. Для меди удельное сопротивление материала обмотки при расчетной температуре:
2.6.7. Активное сопротивление фазы обмотки статора:
Для удобства сопоставления параметров отдельных машин и упрощения расчета характеристик параметры асинхронной машины выражают в относительных единицах, принимая за базисные значения номинальное фазное напряжение и номинальный фазный ток статора. 2.6.8.Относительное значение R1:
Относительные значения одних и тех же параметров схемы замещения различных асинхронных двигателей нормального исполнения незначительно отличаются друг от друга. 2.6.9. Активное сопротивление фазы обмотки ротора r2. Находим как сумму потерь в стержне и участках замыкающих колец. Для литой алюминиевой обмотки ротора удельное сопротивление материала при расчетной температуре:
определяем сопротивление стержня rc:
2.6.10. Сопротивление участка замыкающего кольца, заключенного между двумя соседними стержнями rкл:
2.6.11. Активное сопротивление фазы обмотки ротора:
2.6.12. Сопротивление r2 для дальнейших расчетов должно быть приведено к числу витков первичной обмотки статора:
2.6.13. Относительное значение R2:
Для определения индуктивного сопротивления фазы обмотки статора необходимо определить коэффициенты магнитной проводимости.
2.6.14. Коэффициент магнитной проводимости лобового рассеяния:
2.6.15. Коэффициент ξ. Для определения магнитной проводимости дифференциального рассеяния при полузакрытых или полуоткрытых пазах статора с учетом скоса пазов:
где для βск=0, т.к. отсутствует скос пазов и
2.6.16. Коэффициент магнитной проводимости дифференциального рассеяния для обмоток статора λд1:
2.6.17. Коэффициент магнитной проводимости пазового рассеяния для обмоток статора λп1. Определяется в зависимости от конфигурации пазов по формулам табл. 39: h3=h1c; h2=0;
2.6.18. Индуктивное сопротивление фазы обмотки статора:
2.6.19. Относительное значение х´1:
Для определения индуктивного сопротивления фазы обмотки ротора х2 необходимо определить коэффициенты магнитной проводимости. 2.6.20. Коэффициент магнитной проводимости пазового рассеяния обмотки короткозамкнутого ротора λп2. Рассчитывают по приведенным в табл. 43 формулам в зависимости от конфигурации паза ротора на рис. 17.
где
Для рабочего режима kд=1.
2.6.21. Коэффициент магнитной проводимости лобового рассеяния обмотки короткозамкнутого ротора λл2. В роторах с литыми обмотками при замыкающих кольцах, прилегающих к торцам сердечника ротора:
2.6.22.Коэффициент магнитной проводимости дифференциального рассеяния обмотки короткозамкнутого ротора λд2. Находим с учетом коэффициента ξ:
Δz – находят по кривым рис. 18.
Тогда:
2.6.23.Суммарное значение коэффициентов магнитной проводимости обмоток и короткозамкнутого ротора Σλ2:
2.6.24.Индуктивное сопротивление фазы обмотки статора х2:
2.6.25. Сопротивление х2 для дальнейших расчетов должно быть приведено к числу витков первичной обмотки статора:
2.6.26. Относительное значение Х2:
Расчет потерь.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 1805; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.172.250 (0.011 с.) |

 ;
; ;
;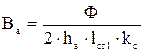 ;
; ;
;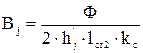 ;
; ;
; ;
; ;
;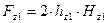 ,
, 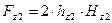 ;
; ;
; ;
;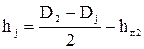 ;
; ;
; ;
; ;
; ;
;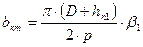 ;
; ;
; Ом·м;
Ом·м;
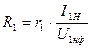 ;
; Ом·м;
Ом·м;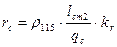 ;
;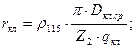
 ;
; ;
; ;
;
 ;
; ;
; =1,256 по табл. 38, 39 определяем k´ск;
=1,256 по табл. 38, 39 определяем k´ск;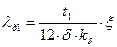 ;
; ;
; ;
;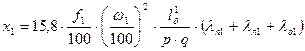 ;
; ;
; ;
; .
. ;
; ;
;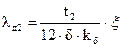 ;
; ;
; ;
; ;
;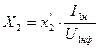 ;
;


