
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принципи аналізу і розрахунку процесівСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Аналіз процесу починається з визначення умов рівноваги системи з урахуванням законів гідродинаміки, термодинаміки і масообміну. Найбільше число параметрів, які можна змінювати, не порушуючи рівноваги, визначають за допомогою правила фаз Гіббса для різних систем
де Ф — число фаз; С — число ступенів свободи, тобто число незалежних змінних, значення яких можна довільно змінювати без порушення числа або складу фаз в системі; К — число компонентів системи. По характерних рівноважних і робочих параметрах визначають рушійну силу процесу, використовувану для розрахунку основних розмірів проектованого апарату. За даними про рівновагу складають матеріальний баланс приходу і витрати речовин в даному процесі
де ∑ Мн і ∑ Мк — число початкових (початкових) і кінцевих речовин відповідно. Зміна теплової енергії системи можна описати рівнянням теплового балансу
де ∑ Qн і ∑ Qк — теплоти, поступаючі в апарат з початковими матеріалами і відводяться з апарату з кінцевими продуктами відповідно; Qp — тепловий ефект процесу (реакція); Qп — втрати теплоти в навколишнє середовище.
За одержаними в результаті вивчення статики і кінетики даними, використовуючи, наприклад, співвідношення (В.1) —(В.З), визначають основний розмір відповідного апарату (площу поперечного перетину, поверхню теплопередачі, діаметр і висоту масообмінного апарату), що є метою здійснюваного технологічного розрахунку. Велику роль при аналізі і розрахунку процесів і апаратів мають їх математичні моделі, які дозволяють цілеспрямовано досліджувати механізм процесу в цілому, вивчати його окремі сторони і явища, вплив початкових параметрів і чинників на його кінцеві результати, а також визначити таке поєднання режимів функціонування, яке забезпечить оптимальні умови його проведення. Проте у ряді випадків математичні моделі, що враховують максимальне число впливаючих на процес величин, настільки ускладнюються, що їх точне рішення стає скрутним, а іноді і взагалі неможливим. Практика інженерної діяльності привела до створення науково обгрунтованого методу, що формує умови проведення експериментів, а також обробки досвідчених даних з можливістю розповсюдження результатів на групу подібних явищ — теорії подібності.
Основи теорії подібності
При розробці нових технологічних процесів і апаратів для їх здійснення дуже часто необхідно використовувати експериментальні дані, що характеризують конкретне виробництво. Досліднику при цьому необхідно вирішити ряд задач. 1. Яким чином від лабораторних результатів і розмірів моделюючого стенду перейти до промислового процесу і установки? 2. Яке мінімальне число величин, що характеризують процес, необхідно вимірювати в ході лабораторного експерименту, не втрачаючи при цьому його фізичної достовірності? 3. Яке мінімальне число експериментів необхідно провести для отримання реальної фізичної картини здійснюваного процесу? На всі ці питання допомагає відповісти теорія подібності, яка встановлює зв'язок між групами подібних явищ. Висновки теорії подібності будуються на підставі аналізу диференціальних рівнянь, що описують досліджуваний процес. Проте одні і ті ж диференціальні рівняння, як правило, описують цілий клас різних по своєму характеру процесів. Для того, щоб розглянути математичну модель явища, що вивчається, необхідно доповнити її параметрами, що конкретизують умови здійснення процесу, що відрізняє його від інших (схожих) процесів. Ці параметри називаються умовами однозначності і включають: • геометричні умови, що характеризують розміри і форму апарату, в якому здійснюється процес;
• фізичні властивості середовищ, що взаємодіють в процесі;
• граничні умови, що характеризують взаємодію середовищ з тілами, що обмежують об'єм протікаючого процесу;
• параметри, що характеризують початковий стан даної системи.
Відповідно до теореми Кірпичова — Гухмана подібні явища, описувані однією і тією ж системою диференціальних рівнянь, у яких дотримується подібність умов однозначності. Звідси витікає, що подібні явища повторюють себе в різних масштабах, що включають геометричну подібність систем, тимчасову подібність, подібність фізичних величин, що характеризують процес, подібність граничних і початкових умов. Таким чином, в подібних процесах повинні виконуватися наступні умови:
• геометрична подібність:
де l1, l2, l3 — характерні розміри першого апарату; L1 L2, L3, — характерні розміри другого апарату, подібні з розмірами першого апарату; Kl — коефіцієнт подібності лінійних розмірів (відповідні кути подібних конструкцій повинні бути рівні);
• часова подібність:
де
• подібність фізичних величин:
де
• подібність початкових і граничних умов припускає постійність відношення основних параметрів на початку і на межі реального процесу і моделі, тобто дотримання геометричної, тимчасової і фізичної подібності. Відношення двох однойменних фізичних величин називається параметричними критеріями, або симплексом. Вибір критеріїв для подібних процесів не є довільним. Покажемо це на прикладі другого закону механіки
де f— сила; m — маса; w— швидкість;
У разі розгляду двох подібних процесів обидва вони описуються рівнянням (В.6), але з різними характерними параметрами
Виражені в безрозмірному вигляді рівняння (2.7) запишуться
Вхідні в них основні змінні в цьому випадку можуть бути виражені відповідно до подібності умов однозначності як
Після підстановки їх у відповідний безрозмірний вираз одержуємо
Оскільки другий співмножник рівний одиниці (рівняння (2.8)), для подібних процесів повинна виконуватися умова:
Якщо замінити в рівнянні (В. 9) коефіцієнти подібності відношенням самих величин, то одержимо
або
Дані безрозмірні комплекси носять назва критеріїв подібності і звичайно позначаються першими двома буквами прізвищ учених, що одержали їх. Так безрозмірний комплекс (2.12) називається критерієм Ньютона.
ри цьому слід пям'ятати, що для подібних процесів самі параметри, що входять в критерії, можуть мінятися в часі і просторі, але в подібних точках об'єму і часу вони приймають одне і те ж значення. При застосуванні теорії подібності розрізняють визначувані і визначаючі критерії. Перші не можна визначити, використовуючи величини, що входять в умови однозначності, другі — можна визначити за допомогою цих величин. Метою проведення і обробки експериментальних досліджень є встановлення функціональної залежності між визначуваними і визначаючими критеріями. Критерії подібності звичайно одержують таким чином: • записують диференціальне рівняння, що описує даний процес (2.6); • приводять його до безрозмірного вигляду шляхом розподілу однієї частини рівняння на іншу, або всіх доданків на одне з вибраних (2. 8); • опускають символи диференціювання. При цьому ступені диференціалів при змінних зберігаються (2.13). Таким чином, аналіз процесу з позицій теорії подібності дозволяє: • визначити впливаючі на процес параметри, які слід вимірювати в ході експерименту; • планувати і проводити експеримент, варіюючи критерії подібності;
• поширювати результати експериментальних досліджень на подібні процеси. При цьому слід пям'ятати, що теорію подібності можна застосовувати тільки до процесів, для яких відомі диференціальні рівняння, що описують їх. Інакше необхідно використовувати інші методи обробки результатів експерименту (методи аналізу розмірностей, регресійний і т.д.).
Лекція 3
|
||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 461; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.131.48 (0.011 с.) |

 (2.1)
(2.1) (2.2)
(2.2) (2.3)
(2.3) (2.4)
(2.4) (2.5)
(2.5) — інтервали часу, характеризуючі стадії першого процесу;
— інтервали часу, характеризуючі стадії першого процесу;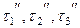 — інтервали часу, характеризуючі схожі стадії подібного процесу;
— інтервали часу, характеризуючі схожі стадії подібного процесу;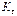 — коефіцієнт часової подібності (гомохронності). При
— коефіцієнт часової подібності (гомохронності). При  = 1 процеси називаються синхронними;
= 1 процеси називаються синхронними; (2.6)
(2.6) — характерні фізичні величини в першому процесі (густина, в'язкість, теплоємність і т.д.);
— характерні фізичні величини в першому процесі (густина, в'язкість, теплоємність і т.д.);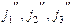 — схожі фізичні величини в другому процесі;
— схожі фізичні величини в другому процесі; — коефіцієнт подібності фізичних величин;
— коефіцієнт подібності фізичних величин; (2.7)
(2.7) — час.
— час. (2.8)
(2.8) (2.9)
(2.9)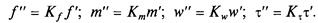
 (2.10)
(2.10) (2.11)
(2.11)
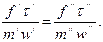 (2.12)
(2.12)
 (2.13)
(2.13)



