Организация мобильного комбинированного урока

Любой урок может быть проведен с использованием электронного средства обучения. Каждый урок должен быть комбинированным по отношению реализуемых на нем продуктивных и репродуктивных видов деятельности, сочетание которых рассматривается в качестве основного признака комбинированного урока. При проведении занятий в компьютерных классах обязательно чередование теоретической и практической работы. Продолжительность занятий с использованием компьютера зависит от возраста учащихся, технических данных компьютера, характера и сложности выполняемой работы.

В соответствии с последними рекомендациями длительность работы за компьютером не должна превышать: на развивающих игровых занятиях для детей 6 лет – 10 мин.; для учащихся (II-IV классов) – 15 мин.; для учащихся V-VII классов, имеющих навыки работы с компьютером, – 20 мин.; на уроках информатики: у учащихся VIII-IX классов – 25 мин.; у учащихся IX – X классов – 40 мин.

Возможные организационные варианты мобильного урока с использованием электронного средства обучения: урок математики проводится в компьютерном классе, причем с компьютерами работает вначале одна часть учащихся, затем другая; урок математики проводится в компьютерном классе, за каждым компьютером находится 2-3 ученика, эта форма используется главным образом при объяснении учителем нового материала для организации фронтальной, коллективной работы. Применение электронных средств обучения возможно также при подготовке и проведении учителем факультативных занятий, организации самоподготовки. Построение урока в компьютерном классе с ротацией групп, работающих за компьютером, приводит к новому понятию – понятию мобильного урока. Мобильность урока позволяет интенсивнее загружать компьютерный класс, тщательнее планировать каждую часть урока, полнее задействовать интерактивные формы обучения. В дополнение к этим рекомендациям учителю необходимо также произвести учет домашних компьютеров своих учащихся и с учетом этого спланировать их домашнюю работу.

2. Технологические и методические аспекты урока. В технологии крупноблочного опережение в изучении теоретического материала (даже в пределах одного параграфа) предполагает выделение для этих целей целиком одного или нескольких уроков.

Рассмотрим первый урок на тему «Признаки равенства треугольников». Содержание учебного материала: определение равных треугольников, формулировки всех трех признаков равенства, доказательство второго признака (заметим, что 1-й признак в нашей системе изложения принят в качестве аксиомы).

 

Цели урока

	В методической форме (для учителя)	В субъектноориентированной форме (для учащихся)
Воспита-тельная	Воспитание активной жизненной позиции и коллективистских качеств в процессе общения учащихся друг с другом, учителем, ЭУ в процессе изучения учебного материала повышенной сложности	Познакомимся с довольно сложным гео-метрическим материалом, усвоение его можно достичь только при вашем актив-ном участии. Можно пользоваться обычным учебником, ШЭУ, или обоими учебниками. Какой вариант выберем?
Развива-ющая	Развитие способности оперировать крупной порцией учебного материала повышенной сложности, развитие памяти и внимания, развитие математической речи	Постараетесь проявить догадку и находчивость. При необходимости с моей стороны и со стороны ШЭУ вам будет оказана необходимая помощь. Договорились?
Образовательная	Обеспечение усвоения учебного материала на уровне понимания и первичного закрепления на основе систематической (пошаговой) обратной связи	Познакомимся с тремя определениями, аксиомой, теоремой и ее доказательством. Этот материал связан с равными треугольниками. Итак, тема урока – «Признаки равенства треугольников»

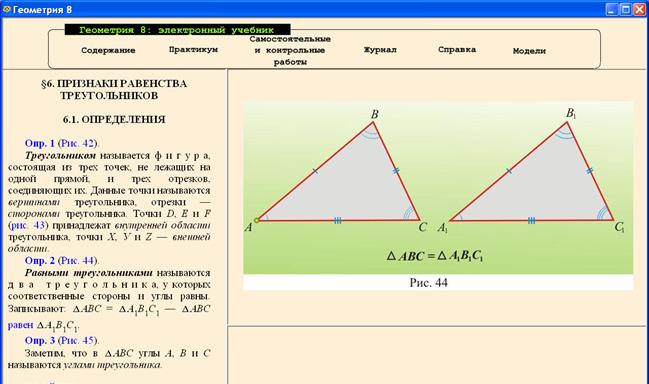
Исходные условия: школьники еще находятся в самом начале изучения систематического курса, у них отсутствует надлежащий опыт в проведении доказательств, доказательство признака является одним из сложных во всем курсе планиметрии. Все это свидетельствует о том, что выбранная порция учебного материала является достаточно крупной и дальнейшее увеличение ее не представляется целесообразным. Формулирование целей урока(таблица 3.3).

Работа с ШЭУ

Вводная часть урока: сообщаются сведения из истории математики, подчеркивается, что признаки равенства треугольников дали исторически первый крупный математический метод доказательства теорем и решения задач, приводятся краткие сведения о Евклиде и его «Началах». В школьном курсе геометрии метод равных треугольников применяется почти «на каждом шагу», поэтому важно каждому ученику овладеть этим методом.

Основная часть урока.

1-й срез: обзор основного содержания урока. Сообщается, что на данном уроке познакомимся с тремя определениями, аксиомой, теоремой и ее доказательством. Перелистываем четыре страницы ЭУ (рис. 3.11-3.12) и показываем, с какими определениями будем знакомиться (называем их и попутно показываем соответствующие рисунки).

2-й срез: образовательная микросреда-1 (признаки микросреды – многократная проработка небольшого фрагмента учебного материала, изучение и закрепление определений с многократной обратной связью): просим одного ученика, пользуясь текстом ШЭУ, вслух прочитать тему урока, название первого пункта темы и первое определение; при коллективном участии класса проводим анализ формулировки (какое понятие определяем, через какое понятие); нескольким ученикам дается задание воспроизвести определение 1 по возможности не подглядывая в экранную страницу; предлагаются аналогичные задания в отношении определений 2 и 3; осуществляется тренировка по воспроизведению всех трех определений.

 

Рисунок 3.11. 1-й срез: обзор основного содержания урока

3-й срез: образовательная микросреда-2 (признаки микросреды – многократная проработка небольшого фрагмента учебного материала, изучение первых двух признаков): один ученик вслух читает по ШЭУ оба признака и воспроизводит их, при необходимости остальные поправляют; после отработки словесных формулировок ученикам предлагается сделать в тетради краткую запись определения равных треугольников и двух признаков равенства.

Примерная запись:

1) ∆ АВС = ∆ А ₁ В ₁ С ₁⇔ (АВ = А ₁ В ₁, ВС=В ₁ С ₁, АС= А ₁ С ₁,

Ð А = Ð А ₁, Ð В = Ð В ₁, Ð С = Ð С ₁) – определение;

2) (АВ = А ₁ В ₁, АС= А ₁ С ₁, Ð А = Ð А ₁) Þ ∆ АВС = ∆ А ₁ В ₁ С ₁ – 1-й признак;

3) (АС= А ₁ С ₁, Ð А = Ð А ₁, Ð С = Ð С ₁) Þ ∆ АВС = ∆ А ₁ В ₁ С ₁ – 2-й признак.

4-й срез: образовательная микросреда-3 (признаки микросреды – использование интерактивной структуризации учебного материала, изучение доказательства 2-го признака с помощью проблемного метода изложения): инициативу проявляет учитель, он обращает внимание учащихся на замысел доказательства (см. ШЭУ), выясняет с учащимися, почему для доказательства теоремы достаточно доказать равенство АВ = А ₁ В ₁, что доказательство будет вестись методом от противного, что для этого строится третий треугольник; б) учитель пользуется проблемным методом изложения, руководит пошаговым предъявлением доказательства, каждый шаг доказательства сопровождается синхронной демонстрацией на рисунке.

Рисунок 3.12. 1-й срез: обзор основного содержания урока