Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сочетание поисковой деятельности с методом системной интерактивной структуризации учебного материалаСодержание книги
Поиск на нашем сайте
Структуризация учебного материалаозначает применение методов и приемов систематизации, позволяющих в явном, непосредственном виде представить структуру учебного материала, излагаемого в любой его форме (текст, графика, цвет, звук). В каждом учебном материале содержаться две главные его компоненты: текст и графика. Под системной структуризацией учебного материала понимают структуризацию текста (посредством нумерации его частей, разграничения этих частей с помощью цвета, голоса, музыкального сопровождения, электронных кнопок перехода от одной части учебного материала к другой и т.д.) и синхронно проводимую структуризацию графического материала, соответствующего этому тексту.Структуризация графического материала отражает последовательность проводимых рассуждений. Эта последовательность может быть отражена на рисунке (чертеже) также нумерацией и одновременно другими средствами, например, пошаговой анимацией, определенной последовательностью цветов линий. Такая многоаспектная структуризация учебного материала позволяет более наглядно н рельефно обнажить структуру учебного материалами, благодаря этому, она оптимальным образом содействует его целостному восприятию. Под системной интерактивной структуризацией учебного материала понимают комплексную структуризацию учебного материала, предоставляющую учащимся возможность самим участвовать в структуризации учебного материала: структурированный текст дополнить структурированным рисунком, по структурированному рисунку воспроизвести текст, при помощи частично структурированного рисунка догадаться, как провести полное рассуждение и т.д. Важным приемом интерактивной структуризации является предоставление учащимся возможности по своему усмотрению вызывать учебный материал дробными или укрупненными порциями. Дополнительные возможности интерактивной структуризации появляются за счет использования интерактивной доски, позволяющей делать записи поверх страницы ШЭУ. Приведем некоторые технологические приемы применения системной интерактивной структуризации учебного материала. а)Приемы применения системной интерактивной структуризации при изложении теоретического материала(на примере учебной темы «Признаки равенства треугольников»). Обратимся ко 2-му признаку равенства треугольников. Теорема(2-йпризнак равенства треугольников). Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого, то такие треугольники равны. Текст доказательства структурируется: римской нумерацией – крупные части доказательства, арабской нумерацией – отдельные шаги доказательства. Обеспечивается пошаговый вызов доказательства. Соответственно нумерации текста проводится интерактивная структуризация графики – визуальная подсказка доказательства: на рисунке нумерацией показывается последовательность рассуждений. Используется также система цветовых выделений. Это создает условия для проявления догадки, организации креативного диалога с целью выяснения общего замысла и плана доказательства. б)Приемы сочетания поисковой деятельности с методом системной интерактивной структуризации (на примере учебной темы «Геометрические задачи на построение»). Задача. Дан D AВС. Постройте D A 1 B 1 C 1, равный D АВС (рисунок здесь опускается). Использование 3d-демонстрации в качестве визуальной подсказки решения задачи – в автоматическом режиме показывается 3d-демонстрация: предварительно перед учащимися ставится цель догадаться с помощью этой демонстрации, какие построения и в какой последовательности нужно выполнить для решения данной задачи. После этого проводится креативный коллективный диалог, в котором учащиеся ставят друг другу вопросы в целях выработки интеллектуальных навыков и навыков креативного поведения:
Проводим закрепление (рефлексию) процесса поиска. С этой целью обращаемся к тексту электронной страницы, в котором излагается в кратком виде поиск, без нумерации шагов поиска, без указания метода поиска. Учащимся ставится задание: пронумеровать в этом тексте шаги поиска и устно указать, каким методом поиска пользовались.
18. Обучающие тестовые задания как средство управления процессом решения геометрических задач. Методические приемы обновления системы задач в целях усиления их воспитательного потенциала Обучающее тестовое задание в отличие от теста для контроля, как правило, содержит помощь. Именно благодаря этому оно является обучающим и выступает средством управления процессом решения задачи. Как и обычно, тестовое задание решается устно или письменно (в обычной тетради). В случае затруднения ученик может обратиться к предлагаемой помощи в ШЭУ. После решения тестового задания ученик указывает свой вариант ответа. К задачам на доказательство и построение предлагаютсяварианты промежуточного ответа. Что касается контролирующей функции ШЭУ, то она должна дополняться контролем со стороны учителя (записано ли решение задачи в тетради ученика, доведено ли решение
Тестовое задание. Докажите, что для любого прямоугольного треугольника с катетами а и b и гипотенузой с справедливо неравенство: а + b Помощь. Дополнительные геометрические построения не помогут. Выполните следующие преобразования и получите очевидное неравенство (2): a + b ≤ c Так как неравенство (2) выполняется очевидным образом, то неравенство (1) также выполняется. Самоконтроль. Неравенство (2) имеет вид: а) (a + b)2 ≥ 0; б) (a – b)2 ≥ 0; в) a 2 – b 2 ≥ 0; г) (b – a)2 ≥ 0.
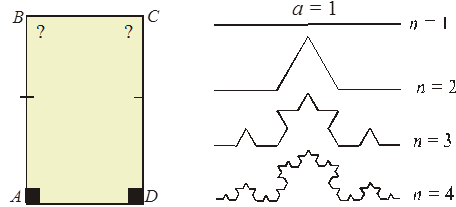
задачи до конца, совершена ли ошибка, на каком шаге ре-шения и т.д.). Выше приведен пример обучающего тестового задания со сравнительно большой помощью. Управление поиском в данном случае может быть охарактеризовано как жесткое управление. Методические приемы обновления системы задач в целях усиления их воспитательного потенциала. Подлинный интерес к учебному предмету, хотя и труднее, необходимо создавать на том материале, который является обязательным и предусмотрен Программой. В этом плане система задач требует обновления. Возможные примеры. Пример 1. Элементы геометрии порядка считаются формальными излишествами и часто избегаются в учебниках. Конечно, теоретизации здесь недопустимы, но интересные задачи возможны. Полезно познакомить учащихся (без доказательства) с теоремой Жордана, рассмотреть рисунки невыпуклых многоугольников, в которых становится неочевидным, принадлежит ли точка внутренней или внешней области (рис. 3.7). Удивление учащихся вызывает тот факт, что решение этого вопроса связывается с нечетностью или четностью точек пересечения произвольного луча, выходящего из данной точки, со сторонами многоугольника. Задание 1. Установите, какие точки принадлежат внутренней области многоугольника, а какие – внешней (рис. 3.7, а). Задание 2. Закрасьте внутреннюю область многоугольника (ответ на рис. 3.7, б). Задание 3. Закрасьте внешнюю область многоугольника (ответ на рис. 3.7, в). Пример 2. Эмоциональное состояние, в котором присутствует удивление, – признак проявления большого интереса. Предложим рассмотреть проблему четырехугольника Саккери (рис. 3.8, ее формулировка – типичная школьная задача) в специально выбранном месте: после изучения признаков равенства треугольников, но раньше изучения свойств параллельных прямых. Можно доказать равенство некоторых треугольников, равенство диагоналей четырехугольника, равенство углов при верхнем основании. Визуально очевидно, что данный четырехугольник является прямоугольником. Делаются различные попытки доказать, что углы при верхнем основании – прямые. Однако все эти попытки отвергаются (в них обнаруживается ошибка). Каково же удивление учащихся, когда им сообщается, что в данном месте курса решить проблему Саккери невозможно.
а) б) в) Рисунок 3.7 – К теореме Жордана
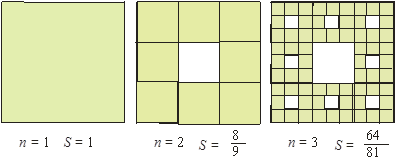
Рисунок 3.8 – К проблеме Саккери Рисунок 3.9 – Пример фрактала: кривая Коха Вернемся к проблеме Саккери через 1-2 урока, после изучения свойств параллельных прямых (начинает работать аксиома параллельных) и неожиданно обнаруживаем, что ранее неразрешимая проблема оказывается легко решаемой. Учащиеся проявляют неподдельный интерес, одновременно с этим на доступной, содержательной и весьма поучительной задаче знакомятся с ролью аксиом в геометрии. Пример 3. Фракталы обычно поражают своей красотой, интерес рассмотрения их еще более усиливается, если с ними связать содержательные геометрические задачи. При рассмотрении кривой Коха (построение ее показано на рис. 3.9) возможны задачи на вычисление длины этой кривой при заданной длине исходного отрезка и некоторого числа итераций построений. Непосредственными вычислениями находится длина кривой для n = 2; 3. Обнаруживается закономерность (длина кривой для n = 2 равна Пример 4. Другим примером фракталов может служить группа фракталов, сыгравших в математике значительную роль в обобщении понятия линии (квадрат Серпинского, кривая Пеано и др.). Обратимся к квадрату Серпинского (рис. 3.10): исходный единичный квадрат разбивается на девять квадратов и удаляется квадрат, находящийся в центре; с оставшимися восьмью квадратами повторяются эти же действия и т.д. Процесс продолжается неограниченно. В связи с этим фракталом учащимся полезно предложить следующую задачу: записать последовательность площадей остающихся частей квадрата. С помощью вычислений приходим к следующей последовательности: 1,
Рисунок 3.10 – Пример фрактала: квадрат Серпинского
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 329; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.165.235 (0.006 с.) |

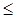 c
c 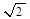 .
.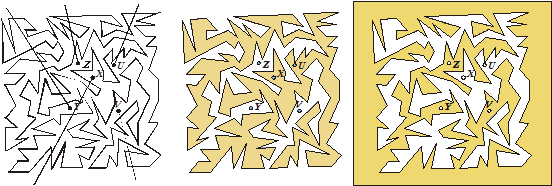
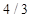 , для n = 3 равна
, для n = 3 равна 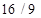 ). Высказывается предположение, что для n = 4 длина равна
). Высказывается предположение, что для n = 4 длина равна 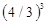 . Это предположение подтверждается непосредственными вычислениями. Индуктивным путем получается формула ln =
. Это предположение подтверждается непосредственными вычислениями. Индуктивным путем получается формула ln = 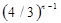 . Обоснование формулы в общем виде может быть рассмотрено при ознакомлении в алгебре с геометрической прогрессией.
. Обоснование формулы в общем виде может быть рассмотрено при ознакомлении в алгебре с геометрической прогрессией.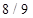 ,
, 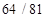 ,…,
,…, 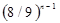 ,… Видно, что при n →
,… Видно, что при n → 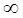 «остаточная» площадь квадрата Sn → 0, что характерно для линии («дырявый» квадрат превращается в своеобразную геометрическую «паутину»).
«остаточная» площадь квадрата Sn → 0, что характерно для линии («дырявый» квадрат превращается в своеобразную геометрическую «паутину»).