
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гальвани-потенциал на границе двух металловСодержание книги
Поиск на нашем сайте
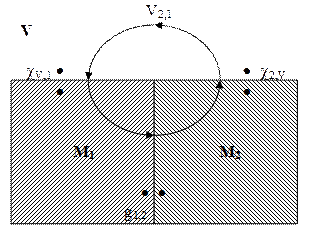
Электродный потенциал представляет собой сложную величину, определяемую тремя отдельными скачками потенциала: скачком потенциала на границе металл электрода – платина и скачками потенциала на границах металл – раствор и платина – раствор. Теория возникновения электродного потенциала должна основываться поэтому на определённых представлениях о природе как скачка потенциала между двумя металлами, так и скачка потенциала на границе металл – раствор. Рассмотрим вначале гальвани-потенциал g1,2 между двумя металлами. Соотношение, существующее между вольта- и гальвани-потенциалами, можно найти, используя правило, по которому сумма всех работ переноса элементарного заряда по замкнутому контуру равна нулю (см. рис. 18): cV,1 + g1,2 + c2,V + V2,1 = 0, g1,2 = V1,2 + c1,V – c2,V. (3)
Работа переноса частицы i с зарядом z F из одной фазы в другую определяется, как известно, разностью электрохимических потенциалов этой заряженной частицы в двух фазах:
В условиях равновесия g1,2 = ( Если обе фазы – металлы, то в обмене между ними участвуют электроны, заряд которых zi F = – F. Для этого случая можно написать g1,2 = Уравнение (6) могло бы служить основой для расчёта гальвани-потенциала, если бы были известны химические потенциалы электронов в двух фазах. Однако, как уже отмечалось, определить для заряженных частиц изменение только химических потенциалов невозможно, поскольку при их переносе из одной фазы в другую одновременно с химической работой совершается также и электрическая. Получим выражение для вольта-потенциала между фазами 1 и 2: подставим значение g1,2 из уравнения (3) в уравнение (4):
( V1,2 = Для частного случая контакта двух металлов V1,2 = (w е – работа выхода электрона из металла). Работа выхода электрона доступна непосредственному экспериментальному определению, и поэтому при помощи уравнения (8) можно рассчитать величину вольта-потенциала. Чем меньше работа выхода электрона из данного металла, тем при данной температуре большее число электронов может покинуть металл и перейти в вакуум и тем положительнее будет заряд обкладки дипольного слоя в металле. Если сблизить два металла с различными работами выхода, то электроны будут переходить от металла с меньшей работой выхода к металлу с большей. В результате этого первый металл зарядится положительно, а второй – отрицательно. Например, для пары Cu½Zn VCu, Zn = 0,3 В, тогда как ЭДС системы Zn½ZnSO4½CuSO4½Cu равна 1,11 В. Таким образом, потенциал V1, 2 составляет заметную долю обратимой ЭДС электрохимической системы. Гальвани-потенциал на границе металл – раствор Осмотическая теория Нернста Первая количественная теория электродного потенциала была предложена Нернстом в 1890 г.; она получила название осмотической теории электродного потенциала и ЭДС. Теория Нернста сыграла большую роль в развитии электрохимии. Она основана на следующих принципах: 1. Электродный потенциал определяется скачком потенциала на границе металл – раствор, а ЭДС электрохимической системы представляет собой разность двух таких скачков потенциала. 2. Электродный потенциал возникает только в результате обмена ионами между металлом и раствором. 3. Движущими силами обмена ионами являются осмотическое давление растворённого вещества p и электролитическая упругость растворения металла Р. Первый принцип нельзя считать верным, поскольку скачок потенциала на границе металл – раствор в общем случае не совпадает с электродным потенциалом, а представляет собой лишь его некоторую часть. Ошибочно также предположение, что ЭДС электрохимической системы всегда равна разности двух гальвани-потенциалов. Она определяется не двумя, а тремя скачками потенциала, включая потенциал, возникающий в месте контакта двух разных металлов. Таким образом, теорию Нернста нельзя считать теорией электродного потенциала и ЭДС. Это – теория гальвани-потенциала металл – раствор, то есть того слагаемого электродного потенциала и ЭДС, которое зависит от состава раствора. Второй принцип находится в согласии с вероятным механизмом возникновения равновесного скачка потенциала на границе металл – раствор, хотя обмен ионами не исчерпывает всех возможных причин, приводящих к образованию скачка потенциала на этой границе. Справедливость предположения об обмене ионами между металлом и раствором в ходе установления равновесного потенциала (и при его достижении) была доказана впоследствии многими исследованиями с помощью меченых атомов. При помощи этого, а также ряда других методов удалось не только подтвердить сам факт обмена ионами, но и количественно оценить его. Поскольку в обмене участвуют заряженные частицы, то его интенсивность можно выразить в токовых единицах и охарактеризовать токами обмена Iо . Токи обмена относят к 1 см2 (1 м2) поверхности раздела электрод – раствор; они служат кинетической характеристикой равновесия между электродом и раствором при равновесном значении электродного потенциала и обозначаются io. Интенсивность обмена зависит от материала электрода, природы реакции и изменяется в широких пределах. По третьему принципу осмотической теории Нернста токи обмена возникают в результате существования сил осмотического давления раствора и электролитической упругости растворения металла. С помощью указанных принципов Нернст получил качественную картину возникновения скачка потенциала металл – раствор и вывел количественную зависимость величины этого скачка от состава раствора. Полученное им уравнение имеет вид ЕL|M = – или при использовании соотношения между осмотическим давлением и концентрацией соответствующих ионов (Mz+) p = RT c, вытекающего из теории идеальных растворов, ЕL|M = – ЕL|M = ЕoL|M + (ЕoL|M – нормальный потенциал Нернста). Уравнение (9) называется формулой Нернста для электродного потенциала. Оно внешне не отличается от общего термодинамического уравнения для электродного потенциала применительно к частному случаю электродов 1-го рода. Нормальный потенциал Нернста можно отождествить со стандартным потенциалом, если вместо концентраций в уравнение (9) подставить активности. По теории Нернста нормальный потенциал является простой функцией электролитической упругости растворения металла. Из теории Нернста следует вывод о независимости стандартных электродных потенциалов от природы растворителя, поскольку величина Р, определяющая нормальный, или стандартный, потенциал электрода, не является функцией свойств растворителя, а зависит лишь от свойств металла. Однако ни опыт, ни теоретические соображения не согласуются с подобного рода представлениями, что также приводит к необходимости пересмотра физических предпосылок теории Нернста.
|
||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 608; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.122.90 (0.008 с.) |

 –
–  =
= 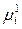 –
– 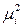 + zi F (
+ zi F (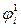 –
–  ) =
) = 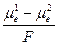 . (6)
. (6) +
+  + zi F V1,2.
+ zi F V1,2.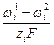 . (7)
. (7) (8)
(8) ln
ln 
 +
+  ,
,


