
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Величины, характеризующие энергетическое состояниеСодержание книги
Поиск на нашем сайте
Величины, характеризующие энергетическое состояние Заряженных частиц Понятие электрохимического потенциала имеет фундаментальное значение при рассмотрении равновесий на границе фаз с участием заряженных частиц (в частности, на границе электрод – раствор). Энергетическое состояние заряженной частицы (i) внутри некоторой фазы (a) характеризуется в общем случае суммой химического потенциала частицы и ее электрической энергии в данной фазе:
(верхний индекс означает фазу).
При равновесии эта разность равна нулю и
что является условием равновесия между фазами a и b, содержащими одинаковые заряженные частицы i. Величину ja можно разложить на два слагаемых: внешний ya и поверхностный ca потенциалы. Соотношения, существующие между различными видами потенциалов, передаются следующей серией уравнений: ja = ya + ca, (2)
Уравнение (4) определяет так называемый реальный потенциал Физический смысл величин, входящих в уравнения (1) – (5), заслуживает особого внимания. Предположим, что проводящая фаза a (металл или раствор электролита) имеет форму сферы и весь ее электрический заряд сосредоточен в тонком поверхностном слое, а заряженная частица i находится в вакууме на бесконечно большом расстоянии от фазы a. Если перенести эту частицу внутрь фазы a, то затраченная работа (после умножения на число Авогадро) даст величину
Чтобы разделить эту работу на «химическую» и «электростатическую» составляющие, предположим, что с фазы a можно мысленно снять заряженный поверхностный слой (см. рис. 10, б). Если в такую пустую заряженную оболочку внести из бесконечности частицу i с зарядом zi e, то нужно затратить работу zi e ja. Умножив эту работу на число Авогадро, получим электростатическую составляющую электрохимического потенциала zi Fja. Работа внесения заряженной частицы i из вакуума внутрь оставшейся незаряженной сферы, при умножении на число Авогадро, дает Величина ja – внутренний потенциал фазы a – аддитивно складывается из внешнего потенциала и поверхностного потенциала. Внешний потенциал ya обусловлен свободными нескомпенсированными зарядами фазы a. Поверхностный потенциал отражает существование двойного электрического слоя на границе фазы; поверхностный потенциал ca обусловлен: для растворов – определенной ориентацией находящихся на поверхности диполей растворителя или растворенных ПАВ (см. рис. 11, 12), а на границе металл – вакуум поверхностный потенциал возникает из-за того, что электронный газ частично смещается относительно ионов кристаллической решетки металла и вместе с их положительными зарядами также образует дипольный слой (см. рис. 13). Если свободный электростатический заряд фазы a равен нулю, то ya = 0 и тогда ja = ca.
Определение потенциалов по уравнениям (1) – (5) относится к фазе в вакууме. Если одна фаза граничит с другой, то для характеристики этой границы необходимо ввести новые понятия, поскольку вследствие взаимного влияния фаз поверхность раздела между ними может отличаться по строению и свойствам от свободных поверхностей исходных фаз. Наряду с внутренними потенциалами фаз j появляется необходимость учитывать их разность на границе раздела фаз: ga,b = ja – jb. (6) Эта разность называется гальвани-потенциалом. Наряду с внешним скачком потенциала y нужно учитывать разность внешних потенциалов открытой части поверхности фаз после частичного (не по всей поверхности) контакта между ними. Эта разность потенциала называется контактным или вольта-потенциалом: Va,b = ya – yb. (7) При создании контакта между фазами возникновение скачка потенциала может быть обусловлено разными причинами, во многом зависящими от природы граничащих фаз. Рассмотрим некоторые простейшие примеры установления электрохимического равновесия на границе раздела фаз. 1. Граница раздела жидких фаз L1 и L2, не содержащих заряженных частиц (см. рис. 14). Возникновение скачка потенциала между фазами (гальвани-потенциала
Одной из наиболее общих причин возникновения скачка потенциала между фазами является обмен заряженными частицами. В момент появления контакта между фазами он протекает преимущественно в каком-то одном направлении, в результате чего создается избыток частиц данного знака заряда по одну сторону границы и их недостаток – по другую. Такой нескомпенсированный обмен приводит к созданию двойного электрического слоя (ДЭС) и к появлению разности потенциалов между фазами. Разность потенциалов, в свою очередь, влияет на кинетику обмена, выравнивая скорость перехода заряженных частиц в обоих направлениях. Наконец, наступает момент, когда уже нет больше преимущественного перехода частиц из одной фазы в другую. Такое значение скачка потенциала отвечает равновесию между фазами, при котором электрохимические потенциалы заряженных частиц в обеих фазах равны. Заряженными частицами, принимающими участие в обмене между фазами, могут быть положительные и отрицательные ионы и электроны. Какие именно частицы переходят из одной фазы в другую, определяется природой граничащих фаз. На границах металл – вакуум и металл 1 – металл 2 такими частицами являются обычно электроны. На границе металл – раствор соли металла в обмене участвуют катионы металла. На границах стекло – раствор и ионообменная смола – раствор в обмене участвуют два вида одноименно заряженных ионов (например, ионы щелочного металла и водорода). При контакте двух несмешивающихся жидкостей, каждая из которых содержит в растворенном виде один и тот же электролит, потенциал возникает за счет неэквивалентного перехода обоих ионов электролита из одной фазы в другую. 2. Граница двух различных металлов. Происходит выравнивание электрохимических потенциалов электронов в металлах: е – (М1) D е – (М2). Условие равновесия имеет вид:
Таким образом, в условиях равновесия работа перенесения электрона из одного металла в другой равна нулю, но работа переноса единицы воображаемого заряда (то есть 3. Граница металл – раствор соли металла. При установлении равновесия происходит выравнивание электрохимических потенциалов ионов металла в растворе и в кристаллической решетке металла: Mz+ (металл М) D Mz+ (раствор L). При равновесии
Поскольку
Уравнение аналогичного типа (вместо активности – концентрация) было впервые получено Нернстом. Таким образом, в условиях рассмотренного электрохимического равновесия работа перенесения иона Mz+ из металла в раствор или обратно равна нулю. Гальвани-потенциал В общем случае гальвани-потенциал между фазами a и b можно представить как сумму трех слагаемых: g a,b = g зар + g адс + g дип, где потенциал g зар обусловлен переходом заряженных частиц, g адс – специфической адсорбцией ионов (на одной или обеих поверхностях), а g дип – ориентацией диполей (на одной или обеих поверхностях). Только при отсутствии всех трех эффектов (или их взаимной компенсации) скачок потенциала между двумя фазами оказывается равным нулю. Осмотическая теория Нернста Первая количественная теория электродного потенциала была предложена Нернстом в 1890 г.; она получила название осмотической теории электродного потенциала и ЭДС. Теория Нернста сыграла большую роль в развитии электрохимии. Она основана на следующих принципах: 1. Электродный потенциал определяется скачком потенциала на границе металл – раствор, а ЭДС электрохимической системы представляет собой разность двух таких скачков потенциала. 2. Электродный потенциал возникает только в результате обмена ионами между металлом и раствором. 3. Движущими силами обмена ионами являются осмотическое давление растворённого вещества p и электролитическая упругость растворения металла Р. Первый принцип нельзя считать верным, поскольку скачок потенциала на границе металл – раствор в общем случае не совпадает с электродным потенциалом, а представляет собой лишь его некоторую часть. Ошибочно также предположение, что ЭДС электрохимической системы всегда равна разности двух гальвани-потенциалов. Она определяется не двумя, а тремя скачками потенциала, включая потенциал, возникающий в месте контакта двух разных металлов. Таким образом, теорию Нернста нельзя считать теорией электродного потенциала и ЭДС. Это – теория гальвани-потенциала металл – раствор, то есть того слагаемого электродного потенциала и ЭДС, которое зависит от состава раствора. Второй принцип находится в согласии с вероятным механизмом возникновения равновесного скачка потенциала на границе металл – раствор, хотя обмен ионами не исчерпывает всех возможных причин, приводящих к образованию скачка потенциала на этой границе. Справедливость предположения об обмене ионами между металлом и раствором в ходе установления равновесного потенциала (и при его достижении) была доказана впоследствии многими исследованиями с помощью меченых атомов. При помощи этого, а также ряда других методов удалось не только подтвердить сам факт обмена ионами, но и количественно оценить его. Поскольку в обмене участвуют заряженные частицы, то его интенсивность можно выразить в токовых единицах и охарактеризовать токами обмена Iо . Токи обмена относят к 1 см2 (1 м2) поверхности раздела электрод – раствор; они служат кинетической характеристикой равновесия между электродом и раствором при равновесном значении электродного потенциала и обозначаются io. Интенсивность обмена зависит от материала электрода, природы реакции и изменяется в широких пределах. По третьему принципу осмотической теории Нернста токи обмена возникают в результате существования сил осмотического давления раствора и электролитической упругости растворения металла. С помощью указанных принципов Нернст получил качественную картину возникновения скачка потенциала металл – раствор и вывел количественную зависимость величины этого скачка от состава раствора. Полученное им уравнение имеет вид ЕL|M = – или при использовании соотношения между осмотическим давлением и концентрацией соответствующих ионов (Mz+) p = RT c, вытекающего из теории идеальных растворов, ЕL|M = – ЕL|M = ЕoL|M + (ЕoL|M – нормальный потенциал Нернста). Уравнение (9) называется формулой Нернста для электродного потенциала. Оно внешне не отличается от общего термодинамического уравнения для электродного потенциала применительно к частному случаю электродов 1-го рода. Нормальный потенциал Нернста можно отождествить со стандартным потенциалом, если вместо концентраций в уравнение (9) подставить активности. По теории Нернста нормальный потенциал является простой функцией электролитической упругости растворения металла. Из теории Нернста следует вывод о независимости стандартных электродных потенциалов от природы растворителя, поскольку величина Р, определяющая нормальный, или стандартный, потенциал электрода, не является функцией свойств растворителя, а зависит лишь от свойств металла. Однако ни опыт, ни теоретические соображения не согласуются с подобного рода представлениями, что также приводит к необходимости пересмотра физических предпосылок теории Нернста. Классификация электродов Если на электроде протекает частная реакция nA A +... + nF = nL L +..., то потенциал электрода определяется уравнением E = Eо + то есть при заданных Т и р определяется (кроме Eо, который является константой) активностями веществ, участвующих в электродной реакции. Характер влияния активностей компонентов раствора на значение E связан с природой электродной реакции и лежит в основе классификации электродов. Принято различать электроды первого рода, второго рода, газовые, окислительно-восстановительные и некоторые специальные типы электродов (амальгамные, третьего рода и др.). Электроды первого рода Электроды первого рода представляют собой металл или металлоид (то есть неметалл с электронной проводимостью), погруженные в раствор своей соли. Электроды первого рода можно схематически представить в виде М n + êМ (если электрод - металл) или в виде Ме n – êМе (если электрод - металлоид). Электродную реакцию записывают как M n + + ne ® M или Me + ne ® Me n –;
(так как активность чистого твердого вещества при заданной температуре постоянна и можно принять ее условно равной 1). Из уравнений следует, что потенциал электрода первого рода зависит от активности лишь одного вида ионов; эти ионы называются потенциалоопределяющими. В случае металлических электродов первого рода такими ионами являются катионы металла, а в случае металлоидных электродов - анионы металлоида. Примеры металлических электродов: металл, погруженный в раствор своей соли (Ag в растворе AgNO3 - Ag+ êAg; Cu в растворе CuSO4 - Cu2+ êCu). Пример металлоидных электродов первого рода - селеновый электрод Se2– êSe. Металлические электроды первого рода имеют большое практическое значение и легче реализуются, чем металлоидные. Следует отметить, что в водных растворах нельзя реализовать как электроды первого рода электроды, обратимые по отношению к ионам щелочных и щелочноземельных металлов, так как в этом случае вместо обратимой реакции разряда-ионизации металла на электроде идет необратимый процесс разложения воды с выделением водорода: Na + H2O = Na+ + 1/2 H2 + OH–. Причина – большое отрицательное значение потенциалов этих электродов. Электроды второго рода Электроды второго рода представляют собой полуэлементы, состоящие из металла, покрытого слоем его труднорастворимого соединения (соли, оксида, гидроксида) и погруженного в раствор, содержащий тот же анион, что и труднорастворимое соединение электродного металла. Схематически электрод второго рода можно представить как A n – êMA êM, а протекающую в нем реакцию MA + ne = M + A n –;
(учитывая, что активности металла и твердого соединения МА постоянны). Таким образом, потенциал электрода второго рода определяется активностью анионов труднорастворимого соединения электродного металла. Однако электроды второго рода обратимы и по отношению к катионам электродного металла: ПРМА =
Из сопоставления потенциалов соответствующих электродов первого и второго рода можно найти ПР труднорастворимых солей. Потенциалы электродов второго рода легко воспроизводимы и устойчивы, поэтому эти электроды часто применяют в качестве электродов сравнения, по отношению к которым измеряют потенциалы других электродов. Наиболее важны в практическом отношении каломельные, ртутно-сульфатные, хлоридсеребряные, ртутнооксидные и сурьмяные электроды. Каломельный электрод. Это ртуть, покрытая пастой из смеси каломели со ртутью, находящаяся в контакте с раствором KCl: Cl– êHg2Cl2 êHg. Электродная реакция: Hg2Cl2 + 2 e = Hg + 2 Cl–; Eкал = Eокал - 2,303 При 25оС Eкал = + 0,2678 - 0,059 lg Eкал определяется активностью ионов Cl–. Наиболее часто употребляются каломельные полуэлементы, в которых концентрация KCl - насыщенный раствор, 1,0 М или 0,1 М. Каломельные электроды, особенно насыщенный, удобны тем, что диффузионный потенциал, возникающий на границе данного раствора с насыщенным KCl, незначителен и во многих случаях его можно не принимать во внимание. Ртутно-сульфатный электрод SO42– êHg2SO4 êHg аналогичен каломельному, ртуть покрыта слоем пасты из ртути и сульфата ртути (I), а в качестве раствора используется H2SO4. При 25оС Eрт.с. = + 0,6156 - 0,0296 lg Хлоридсеребряный электрод представляет собой систему Cl– êAgCl êAg; Eхс = Eохс - 2,303 Ртутно-сульфатный и хлоридсеребряный электроды целесообразно применять в тех случаях, когда исследуемый полуэлемент содержит в качестве электролита либо серную кислоту или сульфаты, либо соляную кислоту или хлориды. Чтобы уменьшить величину диффузионного потенциала, концентрацию этих электролитов в электродах сравнения следует брать такую же, как и в исследуемых полуэлементах. Металлоксидные электроды интересны тем, что здесь в роли анионов труднорастворимого соединения электродного металла выступают ионы гидроксида. К ним относятся, например, ртутнооксидный и сурьмяный электроды: OH– êHgO êHg и OH– êSb2O3 êSb. Уравнения электродных реакций и потенциалов этих электродов: HgO + H2O + 2 e = Hg + 2OH– Eрт.окс. = Eорт.окс. - 2,303 Sb2O3 + 3H2O + 6 e = 2Sb + 6OH– Eсурьм. = Eосурьм. - 2,303 Уравнения для электродного потенциала получены при допущении, что постоянны активности не только соответствующих металлов и их оксидов, но и воды, также принимающей участие в электродной реакции. Металлоксидные электрода второго рода, как и металлсолевые электроды второго рода, обратимы по отношению не только к ионам гидроксила, но и к ионам электродного металла. Кроме того, они обратимы и по отношению к ионам водорода, потому что ионное произведение воды при заданной Т постоянно для любого водного раствора электролита. Металлоксидные электроды можно применять как электроды сравнения в любых растворах кислот и щелочей, однако ртутнооксидный электрод вследствие заметной растворимости оксидов ртути в кислотах можно рекомендовать лишь для растворов с рН > 7. Сурьмяный электрод из-за неустойчивости состава его поверхностного оксида применять как электрод сравнения нельзя; он используется в качестве индикаторного электрода для приближенных определений рН в умеренно кислых и нейтральных растворах. Электроды третьего рода Теоретический интерес представляют электроды третьего рода, где металл находится в контакте с двумя труднорастворимыми солями. В качестве примера электрода третьего рода рассмотрим систему Pb2+ïPbCl2ïAgClïAg, в которой идет электрохимический процесс 2AgCl + Pb2+ + 2 e = 2Ag + PbCl2 . Как видно, при работе электрохимической цепи происходит превращение менее растворимой соли в более растворимую (
Другой пример электрода третьего рода, который ранее использовался для потенциометрического определения катионов Са2+ , – это свинцовый электрод, покрытый слоями труднорастворимых оксалатов свинца и кальция и погруженный в раствор соли кальция. Газовые электроды Газовый электрод представляет собой полуэлемент, состоящий из металлического проводника, контактирующего одновременно с соответствующим газом и с раствором, содержащим ионы этого газа. Конструирование газового электрода невозможно без участия проводника с электронной проводимостью. Требования к металлу в газовых электродах: 1) должен ускорять медленно устанавливающееся электродное равновесие, то есть служить катализатором электродной реакции; 2) потенциал металла в газовом электроде не должен зависеть от активности других ионов раствора, в частности от активности собственных ионов металла; 3) должен быть инертным по отношению к другим возможным реакциям; 4) должен обеспечивать создание максимально развитой поверхности раздела между фазами, на которой могла бы протекать обратимая реакция ионизации газа. Всем этим требованиям лучше всего удовлетворяет платина, электролитически покрытая платиновой чернью (платинированная платина). Газовые электроды очень чувствительны к изменению состояния поверхности платины, особенно к отравлению ее каталитическими ядами. Водородный электрод. Схема электрода: H+ êH2 êPt. Электродная реакция: 2Н+ + 2 е = Н2;
(так как
Таким образом, потенциал водородного электрода определяется не только активностью ионов Н+, но и парциальным давлением газообразного водорода, следовательно, водородный электрод (как и все газовые электроды) более сложен, чем электроды первого и второго рода, потенциалы которых зависят непосредственно от активности частиц одного сорта. Когда парциальное давление водорода равно 1 атм, уравнение упрощается: Другое важное применение газового водородного электрода: при поддержании постоянного значения рН и давления газообразного водорода его можно использовать как электрод сравнения на границе с любыми кислыми и щелочными растворами, причем диффузионный потенциал можно практически свести к нулю подбором соответствующего раствора в водородном электроде. Кислородный электрод. Схема электрода: ОН– êО2 êPt. Электродная реакция: О2 + 2Н2О + 4 е = 4ОН–;
В величину
Однако реализовать обратимый кислородный электрод на практике весьма трудно. Это обусловлено способностью кислорода окислять металлы, даже платину, поэтому на основную электродную реакцию накладывается реакция, отвечающая металлоксидному электроду второго рода. Кроме того, часть кислорода восстанавливается на электроде не до ионов гидроксила, а до ионов перекиси водорода. Поэтому значения потенциала кислородного электрода, полученные опытным путем, обычно не совпадают с теоретическими, и кислородный электрод не используется на практике ни в качестве индикаторного электрода при определении рН, ни в качестве электрода сравнения, хотя теоретически и то и другое возможно. Хлорный электрод. Реализация обратимого газового хлорного электрода Cl– êCl2 êPt связана со значительными трудностями. Теоретически электродная реакция здесь проста: Cl2 + 2 e = 2Cl– и электродный потенциал можно описать уравнением
Однако на основной электродный процесс накладываются побочные реакции с участием хлора. Высокое положительное значение Сравнивая выражения для потенциалов газовых электродов, можно заметить, что при повышении давления соответствующего газа потенциал водородного электрода смещается в отрицательную сторону, а потенциалы кислородного и хлорного электродов – в положительную. Амальгамные электроды Это полуэлементы, в которых амальгама какого-либо металла находится в контакте с раствором, содержащим ионы этого металла: М n + êM m , Hg, m M n + + mne ® M m (Hg). Ртуть ведет себя как инертная среда, в которой растворен металл, а потенциалоопределяющими являются ионы этого металла:
то есть потенциал зависит от активности ионов металла не только в растворе, но и в амальгаме. Если металл находится в ртути в атомарном состоянии (m = 1), то можно написать:
Амальгамные электроды широко применяются в технике и в лабораторной практике. Кадмиевый амальгамный эле
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 432; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.19.136 (0.011 с.) |

 =
=  + zi Fja (1)
+ zi Fja (1) =
=  + zi F(ja – jb).
+ zi F(ja – jb). =
=  , (4)
, (4) ), химический (m) и реальный (a) потенциалы имеют размерность энергии (Дж; эВ); потенциалы – внутренний (j), поверхностный (c) и внешний (y) – имеют размерность электрического потенциала (В).
), химический (m) и реальный (a) потенциалы имеют размерность энергии (Дж; эВ); потенциалы – внутренний (j), поверхностный (c) и внешний (y) – имеют размерность электрического потенциала (В).
 – химический потенциал частицы i в фазе a (рис. 10, в). Химический потенциал представляет собой энергию взаимодействия i -той частицы внутри фазы a с частицами, образующими эту фазу.
– химический потенциал частицы i в фазе a (рис. 10, в). Химический потенциал представляет собой энергию взаимодействия i -той частицы внутри фазы a с частицами, образующими эту фазу.
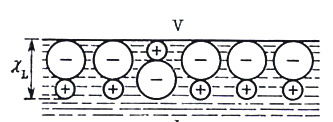

 ) будет обусловлено наложением уже существовавших поверхностных потенциалов
) будет обусловлено наложением уже существовавших поверхностных потенциалов  и
и  . В результате взаимного влияния частиц, образующих двойные электрические слои, возможна перестройка каждого из них с соответствующим изменением поверхностного потенциала. В общем случае поверхностные потенциалы на граничащих фазах не будут совпадать с поверхностными потенциалами на исходных открытых поверхностях фаз:
. В результате взаимного влияния частиц, образующих двойные электрические слои, возможна перестройка каждого из них с соответствующим изменением поверхностного потенциала. В общем случае поверхностные потенциалы на граничащих фазах не будут совпадать с поверхностными потенциалами на исходных открытых поверхностях фаз: ¹
¹  ,
,  ¹
¹  .
.
 на границе двух жидкостей, обусловленный ориентированной адсорбцией диполей жидкостей L1 и L2
на границе двух жидкостей, обусловленный ориентированной адсорбцией диполей жидкостей L1 и L2
 =
=  ,
,  – F
– F  =
=  – F
– F  ,
, =
=  =
= 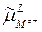 ,
,  + z+FjM =
+ z+FjM =  + z+FjL,
+ z+FjL, = jM – jL = (
= jM – jL = ( + RT ln
+ RT ln  , а
, а  ln
ln  зависит от концентрации потенциалоопределяющих ионов Mz+ и также может быть сведен к нулю.
зависит от концентрации потенциалоопределяющих ионов Mz+ и также может быть сведен к нулю. ln
ln 
 +
+  ,
, ln
ln  ,
, =
= 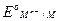 +
+  =
=  ;
; =
=  +
+  =
= 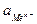

 =
=  + 2,303
+ 2,303  =
= 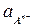
 ;
; lg
lg 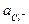 .
. .
. ;
; <<
<<  ). В этой системе потенциал серебра определяется активностью ионов Ag+, активность ионов Ag+ – произведением растворимости
). В этой системе потенциал серебра определяется активностью ионов Ag+, активность ионов Ag+ – произведением растворимости 
 .
. =
=  + 2,303
+ 2,303  lg
lg  = 2,303
= 2,303  - 2,303
- 2,303 
 при всех Т принят равным нулю). При невысоких давлениях газообразного водорода (f ® р) летучесть можно заменить на давление:
при всех Т принят равным нулю). При невысоких давлениях газообразного водорода (f ® р) летучесть можно заменить на давление: .
. =
=  + 2,303
+ 2,303  lg
lg  =
= - 2,303
- 2,303  =
=  + 2,303
+ 2,303 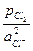 .
. =
=  + 2,303
+ 2,303  lg
lg 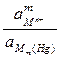 ,
, .
.


