
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Типы задач по расчёту изгибаемых элементовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Прямоугольного сечения При расчёте прочности железобетонных конструкций выделяют два типа задач: I тип – проверка прочности, заданного сечения элемента. II тип – расчёт сечений: а) подбор арматуры при известных размерах сечения элемента под заданный силовой фактор; б) подбор размеров поперечного сечения элемента и арматуры в нём под заданный силовой фактор.
Алгоритм решения задач приведён в таблицах 2 – 4. Таблица 2
Таблица 3
Таблица 4
Расчет изгибаемых элементов таврового сечения
С одиночной арматурой Общие сведения Тавровые сечения встречаются в практике строительства в виде отдельных элементов - балок, а так же в составе конструкций - в монолитных ребристых и сборных панельных перекрытиях. Тавровое сечение состоит из полки – горизонтального и ребра – вертикального элементов. Полка может находиться в сжатой или растянутой зонах (рис. 12, 13). Несущая способность железобетонного элемента не зависит от площади сечения бетона растянутой зоны. Поэтому в сравнении с прямоугольным сечением тавровое сечение значительно выгоднее, т.к. при одной и той же несущей способности бетона расходуется меньше вследствие сокращения размеров растянутой зоны. По той же причине тавровое сечение с полкой в сжатой зоне более целесообразно т.к. полка в растянутой зоне не повышает несущей способности элемента. а) б)
Рис. 12. Тавровые сечения в отдельных балках: а – балка с полкой в растянутой зоне; б – балка с полкой в сжатой зоне
а)
б)
в)
Рис. 13. Тавровые сечения в составе перекрытий а – тавровое сечение пустотной плиты; б – тавровое сечение в составе монолитного ребристого перекрытия; в – тавровое сечение в составе сборного перекрытия
Расчёт изгибаемых элементов таврового сечения С полкой в растянутой зоне
Рис. 14. К расчёту тавровых сечений с полкой в растянутой зоне
В данном случае полка находится в растянутой зоне. Растянутый бетон в расчёте не учитывают, так как в нём имеются трещины. Поэтому расчёт прочности таких элементов выполняют как прямоугольных сечений с размерами
Расчёт изгибаемых элементов таврового сечения С полкой в сжатой зоне При расчётеизгибаемых элементов таврового сечения с полкой в сжатой зоне в зависимости от положения нейтральной оси возможны два случая расчёта: - нейтральная ось находится в пределах полки - нейтральная ось находится в пределах ребра
Определение случая расчёта
Рис. 15. Схема усилий при определении случая расчёта изгибаемых элементов таврового сечения
Предположим, что нейтральная ось проходит по низу полки, т.е. вся полка сжата и тогда Равнодействующие нормальных напряжений в сжатом бетоне и в растянутой арматуре равны:
Плечо внутренней пары сил Рассмотрим равновесие элемента (рис. 15) под действием изгибающего момента от нагрузки 1.
Если Если Данные уравнения применяют для определения случай расчёта тавровых сечений при решении I типа задач – проверки прочности, заданного сечения элемента.
2.
Выражение Если Если Данные уравнения применяют для определения случай расчёта тавровых сечений при решении II типа задач – расчёта сечений элемента.
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 719; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.196.93 (0.008 с.) |

 , где
, где  определяют по чертежу армирования сечения.
4. Определяют высоту сжатой зоны бетона
определяют по чертежу армирования сечения.
4. Определяют высоту сжатой зоны бетона  .
5. Находят относительную высоту сжатой зоны бетона
.
5. Находят относительную высоту сжатой зоны бетона  .
6. Вычисляют граничную относительную высоту сжатой зоны бетона
.
6. Вычисляют граничную относительную высоту сжатой зоны бетона  .
7. Проверяют условие x £ xR.
8. Определяют несущую способность балки Mult.
9. Проверяют условие М≤Mult.
.
7. Проверяют условие x £ xR.
8. Определяют несущую способность балки Mult.
9. Проверяют условие М≤Mult.
 .
3. Определяют
.
3. Определяют  .
4. Вычисляют
.
4. Вычисляют  и
и  .
5. Проверяют условие: x £ xR.
6. Определяют требуемую площадь арматуры
.
5. Проверяют условие: x £ xR.
6. Определяют требуемую площадь арматуры  или
или  , при этом
, при этом 
 .
7. По найденной площади сечения продольной арматуры принимают количество и диаметр рабочих стержней.
8. Выполняют чертёж армирования сечения элемента.
.
7. По найденной площади сечения продольной арматуры принимают количество и диаметр рабочих стержней.
8. Выполняют чертёж армирования сечения элемента.
 = 1-2% для балок,
= 1-2% для балок,  ).
3. Определяют
).
3. Определяют  .
4. Задаются шириной сечения b в зависимости от величины М.
5. Определяют требуемую рабочую высоту сечения
.
4. Задаются шириной сечения b в зависимости от величины М.
5. Определяют требуемую рабочую высоту сечения  .
6. Определяют высоту сечения
.
6. Определяют высоту сечения  (а ≥ 40 мм).
7. Принимают высоту сечения кратно 10 мм для плит; кратно 50 мм для балок при h ≤ 600 мм; кратно 100 мм для балок при h > 600 мм.
8. Проверяют соотношение размеров сечения
(а ≥ 40 мм).
7. Принимают высоту сечения кратно 10 мм для плит; кратно 50 мм для балок при h ≤ 600 мм; кратно 100 мм для балок при h > 600 мм.
8. Проверяют соотношение размеров сечения  . Если размеры
. Если размеры  и
и  не отвечают конструктивным условиям, их уточняют повторным расчётом.
9. Определяют площадь сечения арматуры As (см. тип задачи IIа с п.2).
не отвечают конструктивным условиям, их уточняют повторным расчётом.
9. Определяют площадь сечения арматуры As (см. тип задачи IIа с п.2).



 .
. (1 случай);
(1 случай); >
>  (2 случай).
(2 случай).
 .
. ,
,  .
.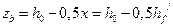 .
. и внутренних усилий, возникающих в сжатом бетоне
и внутренних усилий, возникающих в сжатом бетоне  и растянутой арматуре
и растянутой арматуре 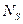 .
. ;
; ;
;  ;
;  .
. , то
, то  >
>  , то
, то  ;
; ;
;  ;
;  .
. представляет собой изгибающий момент, воспринимаемый сжатой полкой.
представляет собой изгибающий момент, воспринимаемый сжатой полкой. , то
, то  , то
, то 


