
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчёт железобетонных конструкций по деформациямСодержание книги
Поиск на нашем сайте
Расчёт по прогибам Расчёт железобетонных элементов по прогибам производят из условия:
где f - прогиб железобетонного элемента от действия внешней нагрузки; fult - значение предельно допустимого прогиба железобетонного элемента по нормам. Прогибы железобетонных конструкций определяют по общим правилам строительной механики в зависимости от изгибных, сдвиговых и осевых деформационных характеристик железобетонных элементов в сечениях по его длине. Для изгибаемых элементов прогиб определяют по формуле: где В общем случае данную формулу можно реализовать путем разбиения элемента на ряд участков, определяя кривизну на границах этих участков (с учетом наличия или отсутствия трещин и знака кривизны) и перемножения эпюр моментов Для изгибаемых элементов постоянного сечения, имеющих трещины на каждом участке, в пределах которого изгибающий момент не меняет знак, допускается вычислять кривизну для наиболее напряженного сечения и принимать для остальных сечений такого участка кривизны изменяющимися пропорционально значениям изгибающего момента (рис. 33). В этом случае для свободно опертых и консольных элементов максимальный прогиб определяют по формуле где S - коэффициент, зависящий от расчётной схемы элемента и вида нагрузки, некоторые значения которого приведены в таблице 15.
Таблица 15
Рис. 33. Эпюры изгибающих моментов и кривизны в железобетонном элементе постоянного сечения а - схема расположения нагрузки; б - эпюра моментов; в - эпюра кривизны Полную кривизну изгибаемых, внецентренно сжатых и внецентренно растянутых элементов для участков без трещин в растянутой зоне определяют по формуле: где Кривизну железобетонного элемента на участке без трещин определяют по формуле где М - изгибающий момент от внешней нагрузки (включая момент от продольной силы N относительно оси, проходящей через центр тяжести приведенного сечения); D - изгибная жесткость приведенного поперечного сечения элемента, определяемая по формуле:
Ired - момент инерции приведенного сечения относительно его центра тяжести; Eb 1 - модуль деформации сжатого бетона, принимаемый: при непродолжительном действии нагрузки Eb 1 = 0,85 Eb; при продолжительном действии нагрузки где φb,cr - коэффициент ползучести бетона, принимаемый в зависимости от относительной влажности воздуха и класса бетона. Полную кривизну изгибаемых, внецентренно сжатых и внецентренно растянутых элементов для участков с трещинами в растянутой зоне определяют по формуле: где Кривизну железобетонного элемента на участке с трещинами определяют по той же формуле: Изгибная жесткость приведенного сечения элемента равна где Ired - момент инерции приведенного сечения относительно его центра тяжести без учёта растянутой зоны бетона; Eb 1 - модуль деформации сжатого бетона, принимаемый равным
Значения относительных деформаций ε b1,red принимают: - при непродолжительном действии нагрузки ε b1,red = 0,0015; - при продолжительном действии нагрузки – в зависимости от относительной влажности воздуха окружающей среды ε b1,red = 0,0024-0,0034. Значение коэффициента приведения арматуры к бетону в данном случае принимают равным
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 387; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.110.45 (0.005 с.) |

 ,
,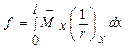 ,
, - изгибающий момент в сечении х от действия единичной силы, приложенной в сечении, для которого определяется прогиб, в направлении этого прогиба;
- изгибающий момент в сечении х от действия единичной силы, приложенной в сечении, для которого определяется прогиб, в направлении этого прогиба;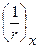 - полная кривизна элемента в сечении от внешней нагрузки, при которой определяется прогиб.
- полная кривизна элемента в сечении от внешней нагрузки, при которой определяется прогиб.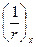 по длине элемента, принимая линейное распределение кривизны в пределах каждого участка.
по длине элемента, принимая линейное распределение кривизны в пределах каждого участка. ,
, - полная кривизна в сечении с наибольшим изгибающим моментом, от нагрузки, при которой определяют прогиб;
- полная кривизна в сечении с наибольшим изгибающим моментом, от нагрузки, при которой определяют прогиб;



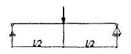
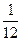


 , где Si и Mi – соответственно коэффициент S и момент M в середине пролета балки или в заделке консоли для каждой схемы загружения.
В этом случае кривизну
, где Si и Mi – соответственно коэффициент S и момент M в середине пролета балки или в заделке консоли для каждой схемы загружения.
В этом случае кривизну 

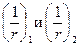 - кривизны соответственно от непродолжительного действия кратковременных нагрузок и от продолжительного действия постоянных и длительных нагрузок.
- кривизны соответственно от непродолжительного действия кратковременных нагрузок и от продолжительного действия постоянных и длительных нагрузок.
 ,
,
 ,
,
 - кривизна от непродолжительного действия всех нагрузок, на которые производят расчет по деформациям;
- кривизна от непродолжительного действия всех нагрузок, на которые производят расчет по деформациям; - кривизна от непродолжительного действия постоянных ивременных длительных нагрузок;
- кривизна от непродолжительного действия постоянных ивременных длительных нагрузок; - кривизна от продолжительного действия постоянных и временных длительных нагрузок.
- кривизна от продолжительного действия постоянных и временных длительных нагрузок. ,
, .
.


