
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нормативное и расчётное сопротивления древесиныСодержание книги Поиск на нашем сайте
Нормативное сопротивление древесины Статическая обработка таких испытаний позволяет определить нормативное сопротивление, для которого доверительная вероятность установлена не ниже 0,95. Это значит из 100% отобранных образцов не менее 95% должны иметь прочность, большую нормативного сопротивления или равную ему. Расчётное сопротивление древесины Расчётное сопротивление древесины получают путём деления нормативных значений сопротивления на коэффициенты надёжности. Модуль упругости древесины вдоль волокон независимо от породы принимается Модуль упругости древесины для учета зависимости от условий эксплуатации и классов длительности нагружения необходимо умножать на значения коэффициента
Лекция 5. Расчёт деревянных элементов Расчёт центрально растянутых элементов Растянутые элементы – это нижние пояса ферм, затяжки арок и стержни других сквозных конструкций. Зависимость древесины при растяжении Прочность растянутых элементов в тех местах, где они ослаблены отверстиями или врезками учитывается снижающим коэффициентом При наличии ослаблений в пределах длины равной 20 см, в разных сечениях, поверхность разрыва всегда проходит через них. Поэтому при определении ослабленной площади сечения
Рис. 5.1. Растянутый элемент: а) схема работы; б) диаграмма деформирования чистой без пороков древесины при кратковременном растяжении; в) схема разрушения; г) эпюры напряжений при наличии ослаблений Расчёт центрально-растянутых элементов по прочности производится по формуле:
где Сжатые элементы На сжатие работают стойки, подкосы, верхние пояса и отдельные стержни ферм и других сквозных конструкций. Древесина работает на сжатие более надежно, чем на растяжение, но не вполне упруго. Примерно до половины предела прочности древесина работает упруго, а рост деформаций происходит по закону, близкому к линейному. При дальнейшем увеличении напряжений деформации растут всё быстрее, чем напряжения, указывая на упругопластическую работу древесины. Разрушение образцов происходит пластично в результате потери местной устойчивости, о чём свидетельствует характерная складка на образце. Поэтому сжатые элементы работают более надёжно, чем растянутые, и разрушаются только после заметных деформаций. Сжатые элементы конструкций имеют длину, как правило, намного большую, чем размеры поперечного сечения и разрушаются не как малые стандартные образцы, а в результате потери устойчивости, которая происходит раньше, чем напряжения сжатия достигнут предела прочности. При потере устойчивости сжатый элемент выгибается в сторону (рис.5.2 (б)). При дальнейшем выгибе на вогнутой стороне появляются складки, свидетельствующие о разрушении древесины от сжатия, а на выпуклой стороне древесина разрушается от растяжения. Расчёт центрально-сжатых элементов производится по формулам: на устойчивость (для элементов с гибкостью
где
Гибкость ( Расчётную длину
Рис. 5.2. Сжатый элемент: а) диаграмма деформирования чистой от пороков древесины; б) схема работы, разрушения и эпюра напряжений; в) типы закрепления концов и расчётные длины Сжатие поперёк волокон. При местном сжатии поперёк волокон соседние незагруженные участки древесины тоже сжимаются за счёт изгиба волокон и оказывают поддерживающее действие работе незагруженного участка, чем меньше его длина В настоящий момент при сжатии поперек волокон должно соблюдаться условие:
Рис.5.3 Сжатие поперек волокон
При наклонном сжатии под углом к направлению волокон (α) должно удовлетворять следующее условие:
Смятие древесины – это поверхностное сжатие, которое может быть местным и общим. Общее смятие – это когда сжимающая сила действует на всю поверхность, местное – когда сила действует на часть поверхности элемента. Смятие древесины в конструкции может происходить: · вдоль волокон; · поперёк волокон; · под углом к волокнам; Сопротивление древесины смятию поперёк волокон в несколько раз меньше сопротивления её вдоль волокон (клетки работают в наименее благоприятных условиях: они сплющиваются за счёт внутренних пустот). Изгибаемые элементы Изгибаемые элементы: балки, настилы, обшивки. В изгибаемом элементе от нагрузок, действующих поперёк его продольной силы, возникают изгибающие моменты От действия изгибающего момента в сечениях элемента возникают напряжения изгиба (рис.5.4), которые состоят из сжатия в верхней половине сечения и растяжения в нижней. Нормальные напряжения в сечениях распределяются неравномерно по высоте. рекомендуется изготавливать из II сорта, в малоответственных элементах III сорт.
Рис. 5.4. Изгибаемый элемент: а) график прогибов; б) схема разрушения и эпюра нормальных напряжений; схема работы при косом изгибе (в); оси элемента (г); эпюра напряжений (д) Расчет изгибаемых элементов, обеспеченных от потери устойчивости, на прочность по нормальным сечениям производят по формуле:
где Для изгибаемых элементов, не имеющих постоянного подкрепления сжатой кромки из плоскости изгиба, следует также провести проверку на устойчивость плоской формы деформирования по формуле:
Косой изгиб. В элементах, оси сечений которых расположены наклонно к направлению действия нагрузок (балки, прогоны скатных покрытий) изгиб можно рассматривать как результат изгибов относительно любой из осей сечения, каждый из которых происходит как прямой. При косом изгибе нормальные напряжения в сечениях суммируются и достигают максимальных значениях в верхних и нижних точках сечения (рис.5.4 (в-д) Проверка прочности косоизгибаемых элементов производится по формулам:
Расчёт косоизгибаемых элементов по прогибам производится с учётом геометрической суммы прогибов относительно каждой оси по формуле:
|
||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 3454; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.1.23 (0.01 с.) |

 (МПа) является основной характеристикой прочности древесины чистых от пороков участков. Эта величина определяется по результатам многочисленных лабораторных кратковременных испытаний малых стандартных образцов сухой древесины влажностью 12% на растяжение, сжатие, изгиб, смятие и скалывание.
(МПа) является основной характеристикой прочности древесины чистых от пороков участков. Эта величина определяется по результатам многочисленных лабораторных кратковременных испытаний малых стандартных образцов сухой древесины влажностью 12% на растяжение, сжатие, изгиб, смятие и скалывание.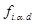 - это основная характеристика прочности реальной древесины, т.к. древесина имеет естественные допускаемые пороки (которых не бывает в лабораторных образцах) и работает под нагрузками в течение многих лет.
- это основная характеристика прочности реальной древесины, т.к. древесина имеет естественные допускаемые пороки (которых не бывает в лабораторных образцах) и работает под нагрузками в течение многих лет. . Это значение получено путём снижения в 1,5 раза модуля упругости (Е= 15000МПа), полученного из кратковременных испытаний образцов древесины; поперек волокон Е90=400МПа.
. Это значение получено путём снижения в 1,5 раза модуля упругости (Е= 15000МПа), полученного из кратковременных испытаний образцов древесины; поперек волокон Е90=400МПа. , а для конструкций, подвергающихся воздействию повышенной температуры, на значение коэффициента
, а для конструкций, подвергающихся воздействию повышенной температуры, на значение коэффициента  .
.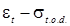 близка к линейной (рис. 5.1), т.к. древесина работает на растяжение как упругий материал. Разрушение растянутых элементов происходит хрупко, в виде почти мгновенного разрыва наименее прочных волокон по пилообразной поверхности без заметных предварительных деформаций.
близка к линейной (рис. 5.1), т.к. древесина работает на растяжение как упругий материал. Разрушение растянутых элементов происходит хрупко, в виде почти мгновенного разрыва наименее прочных волокон по пилообразной поверхности без заметных предварительных деформаций. = 0,8 к расчётному сопротивлению древесины.
= 0,8 к расчётному сопротивлению древесины. все ослабления на этой длине суммируются, как бы совмещаются в одном сечении (рис.5.1(г)).
все ослабления на этой длине суммируются, как бы совмещаются в одном сечении (рис.5.1(г)).
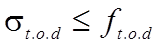 ;
;  (5.1)
(5.1) - расчётная осевая сил;
- расчётная осевая сил; 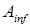 - площадь поперечного сечения элемента нетто.
- площадь поперечного сечения элемента нетто. )
)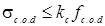 (5.2)
(5.2) ;
;  - расчётная площадь поперечного сечения, принимаемая равной:
- расчётная площадь поперечного сечения, принимаемая равной:  - площади сечения брутто, если ослабления не выходят за кромку и площадь ослабления не превышает 25%;
- площади сечения брутто, если ослабления не выходят за кромку и площадь ослабления не превышает 25%;  - площади сечения нетто, если ослабления не выходят за кромку и площадь ослабления превышает 25%;
- площади сечения нетто, если ослабления не выходят за кромку и площадь ослабления превышает 25%; 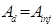 - площади нетто, если ослабления выходят за кромки;
- площади нетто, если ослабления выходят за кромки; - коэффициент продольного изгиба, определяемый в зависимости от гибкости элемента:
- коэффициент продольного изгиба, определяемый в зависимости от гибкости элемента: ) зависит от расчётной длины элемента и радиуса инерции сечения элемента в направлении соответствующей оси (
) зависит от расчётной длины элемента и радиуса инерции сечения элемента в направлении соответствующей оси ( );
); следует определять умножением его свободной длины (
следует определять умножением его свободной длины (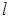 ) на коэффициент (
) на коэффициент (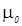 ), учитывающий закрепление элемента и нагрузку, действующую на элемент (рис.5.2(в)).
), учитывающий закрепление элемента и нагрузку, действующую на элемент (рис.5.2(в)).
 (5.6)
(5.6) - коэффициент, учитывающий поддерживающие влияния волокон при сжатии поперёк волокон на участке; зависит от величины
- коэффициент, учитывающий поддерживающие влияния волокон при сжатии поперёк волокон на участке; зависит от величины  ,
,  (рис. 5.3).
(рис. 5.3).
 , где расчётное сопротивление сжатию под углом определяется по формуле
, где расчётное сопротивление сжатию под углом определяется по формуле (5.7)
(5.7) и поперечные силы
и поперечные силы  .
.

 (5.8)
(5.8) - расчетное сопротивление изгибу;
- расчетное сопротивление изгибу;  - расчетное напряжение.
- расчетное напряжение. (5.9)
(5.9) (5.12)
(5.12) (5.13)
(5.13)


