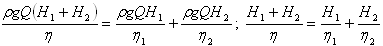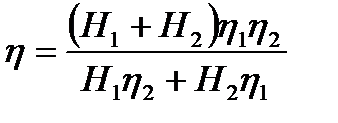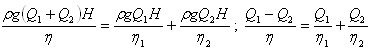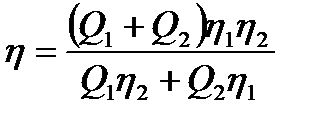Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формула Дарси-Вейсбаха. Коэффициент гидравлического сопротивления. Режимы течения. Формулы для расчета коэффициента гидравлического сопротивления. Формула Л.С. Лейбензона для расчета потерь напора.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Формула Дарси-Вейсбаха
1) Ламинарный режим течения, при котором Re<2320. Формула Стокса: Ламинарный режим бывает при перекачке вязкой нефти. Зона гидравлически гладких труб, в которой Зона смешанного трения, в которой Формула Альтштуля: Зона квадратичного трения, в которой Формула Шефринсона Формулы Стокса, Блазиуса и Шефренсона имеют следующий общий вид:
А, m =const m – показатель режима движения жидкости Подставим (1) в формулу Дарси-Вейсбаха, учитывая, что получили общую формулу Лейбензона
Формула Лейбензона широко применяется в тех случаях, когда зависимость
На графике зависимость В области смешанного трения λ зависит не только от Re, но и от относительной шероховатости
Линия Показатель режима течения m в этой области – переменная величина. Однако ценой некоторой потери в точности расчетов этот недостаток может быть устранен. Отметим на графике цифрой 1 – точку на прямой Блазиуса, где Re1=10(K/D)-1 цифрой 2 – точку на прямой Шифринсона, где Re2=500(K/D)-1 подставив Re1 в формулу Блазиуса, а Re2 в Шифринсона, найдем lgλ1 и lgλ2 – ординаты (.) 1 и 2, Затем проведем через эти точки прямую. ее уравнение приводится к виду
33.Уравнение баланса напоров для участка трубопровода. Напорно - расходные (Q-Н,)- характеристики трубопровода.
Для магистрального нефтепровода постоянного диаметра с n перекачивающими станциями, уравнение баланса напоров имеет вид
В начале каждого эксплуатационного участка ПС оснащены подпорными насосами. В конце трубопровода и каждого эксплуатационного участка требуется обеспечить остаточный напор hОСТ для преодоления сопротивления технологических трубопроводов и закачки в резервуары. Правая часть уравнения (1.34) представляет собой полные потери напора в трубопроводе, то есть Н. В случае наличия вставок или лупингов по трассе правая часть уравнения (1.34) определяется по формуле (1.32). Левая часть уравнения (1.34) – суммарный напор, развиваемый всеми работающими насосами перекачивающих станций (активный напор). С помощью коэффициентов характеристик насосов активный суммарный напор может быть представлен зависимостью
где mМ – количество работающих магистральных насосов на одной ПС; mП – количество работающих подпорных насосов на ГПС (или на ПС в начале эксплуатационного участка), включенных параллельно; аП, bП, hП – коэффициенты характеристики и напор, развиваемый подпорным насосом при подаче Q; аМ, bМ, hМ – то же для магистрального насоса. Обозначив
можно записать
Выразив левую часть уравнения (1.34) через (1.35), а правую часть – через (1.30), получим уравнение баланса напоров в аналитической форме
Раскрывая скобки и решая уравнение (1.37) относительно расхода, имеем
Если в общем случае на линейной части имеются лупинги и вставки, уравнение (1.38) примет вид
Определив расход Q, можно вычислить напор, развиваемый перекачивающими станциями, а также суммарные потери напора в трубопроводе. Обе эти величины одинаковы (условие баланса напоров). Тот же результат можно получить графически, построив совмещенную характеристику трубопровода и насосных станций. Точка пересечения характеристик называется рабочей точкой (А), которая характеризует потери напора в нефтепроводе и его пропускную способность при заданных условиях перекачки (рис. 1.12). Равенство создаваемого и затраченного напоров, а также равенство подачи насосов и расхода нефти в трубопроводе приводят к важному выводу: трубопровод и перекачивающие станции составляют единую гидравлическую систему. Изменение режима работы ПС (отключение части насосов или станций) приведет к изменению режима нефтепровода в целом. Изменение гидравлического сопротивления трубопровода или отдельного его перегона (изменение вязкости, включение резервных ниток, замена труб на отдельных участках трассы и т. п.) в свою очередь окажет влияние на режим работы всех перекачивающих станций. 34.Трубопроводы с промежуточными перекачивающими станциями, работающими в режиме "из насоса -в насос". Система гидравлических уравнений для расчета расхода перекачки и подпоров перед промежуточными станциями. Уравнение баланса напоров для трубопровода. Условия "согласования" работы последовательных участков трубопровода.
- полн. напор на выходе из НПС в начале участка (где z1 – высот. отметка начала участка; hп - подпор на входе в НПС; Hст(Q) – дифф. напор НПС)
(где z2 – выс. отметка конца участка; hк – остат. напор в конце участка.) ур. Бернулли примет вид: Преобразовав его, получим: – ур. баланса напоров для уч-ка н/п. Оно служит для определения расхода перекачки Q. В этом ур. левая часть При перекачке по схеме «из насоса в насос» конец предыдущ.перегона м/ду станциями явл. сечением всасывания следу-й ПС. Перегоны н/п м/ду послед. соед-ми ПС оказ-ся в гидравлич. отношении жестко связ-ми друг с другом (изм-е режима работы одного перегона скажется на режиме работы всего н/п)
Рассм. н/п с n нефтеперекач. станциями. Запишем систему из n ур. баланса напоров для каждого уч-ка: (где z1 – выс.отметка начала т/п; z2 – выс. отметка конца т/п; hп –подпор на входе в НПС; hк – остат. напор в конце т/п; Нст(Q) – дифф. напор НПС) Сложив все уравнения получим: - ур. баланса напора для всего т/п. Левая часть С помощью системы можно опр. величину подпоров на входе в каждую НПС: Cложив первые m ур-ний системы можно получить подпор перед m-ой НПС: Зная его можно вычисл. давл. на входе m -ой НПС. Условия «согласования» работы Н/п 1)Величина подпора на любой станции должна больше величины анти кавитац. запаса работы насоса, то есть hn1>hкавi 2)Давление на нагнетат. линии любого насоса должно превосходить давление, опр. прочностью труб и корпуса насоса, то есть pn1>pпрочi
Напорно-расходные (Q-Н)- характеристики перекачивающих станций. (Q-Н)- характеристики станций, оснащенных центробежными нагнетателями. Мощность насосных агрегатов. Формулы для расчета мощности. Коэффициент полезного действия.
НПС устанавливается несколько насосов. Суммарная (Q-H)-хар-ка НПС – суммар. хар-ки всех насосов, включ. последоват. и параллельно, а также хар-ки станционных т/п станции. Чаще всего, на НПС насосы включены последовательно для повышения напора. Для перекачки нефтей исп-ют, в основном, центробежные насосы, в кот. необх-й напор создается за счет центробежной силы. Гидравл. хар-ка центробеж. насосов представляют двухчленной зависимостью H=a-bQ2; а – нагнетание насоса при нулевой подаче, в – крутизна параболы
Нсм=Нсум(Q)-hст(Q) Нст(Q)- суммар. хар-ка насосов, установл. на станции; hст(Q) – хар-ка станционных т/п. Полезная мощность центробежного насоса – мощность, расходуемая на преодоление разности напора между нагнетанием и всасывание насоса.
Мощность, затрачиваемая насосным агрегатом (Q-η) хар-ка насоса: η=kQ-k1Q2 Зави-ть КПД насоса от подачи Насосы подбирают таким образом, чтобы рабочая подача была при максимальном КПД. При послед. соед-ии насосов КПД опр-ся из системы
При парал. соед-ии насосов КПД опр. из системы:
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 2493; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.237.169 (0.007 с.) |



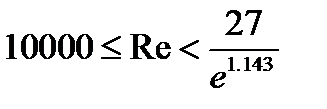 . Ф-ла Блазиуса:
. Ф-ла Блазиуса: 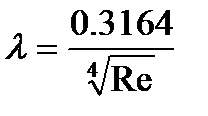
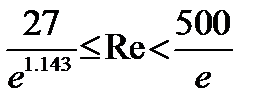
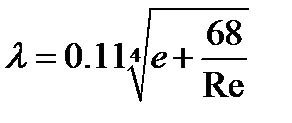
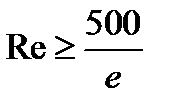
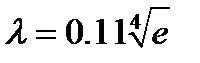
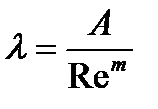 (1)
(1)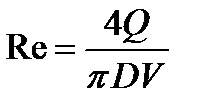 ,
,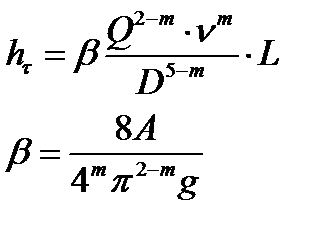
 от расхода должна быть выражена в явном виде
от расхода должна быть выражена в явном виде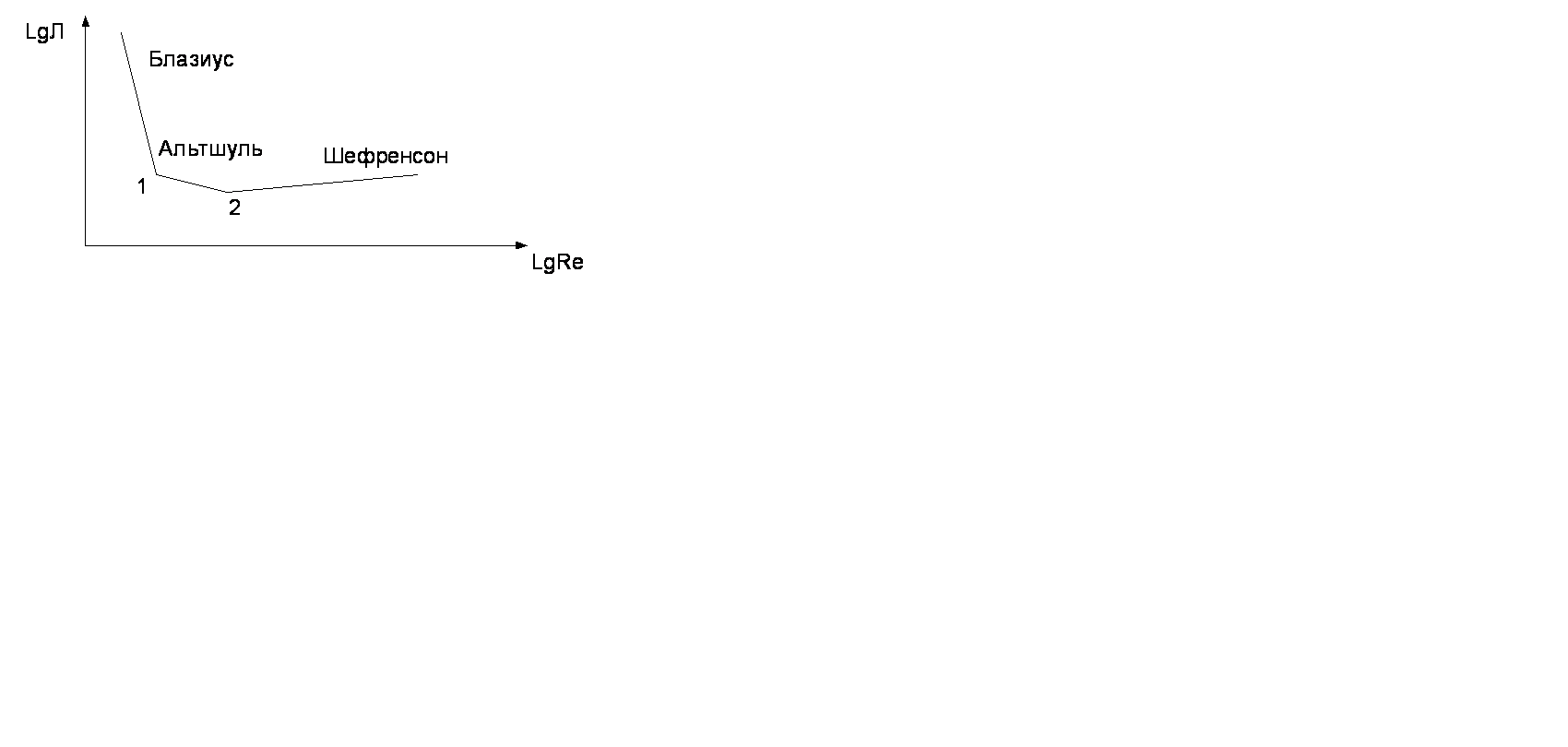

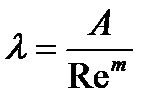 для режим течения выглядит в виде прямых линий, tg угла наклона которого к оси LgRe tg=m
для режим течения выглядит в виде прямых линий, tg угла наклона которого к оси LgRe tg=m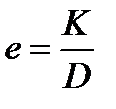
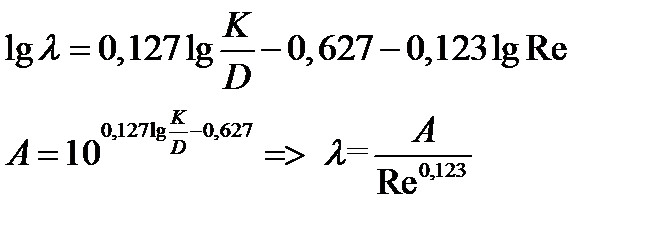
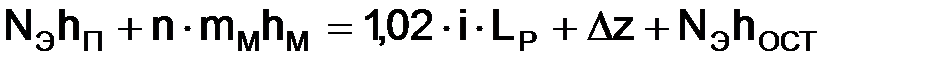 . (1.34)
. (1.34) , (1.35)
, (1.35)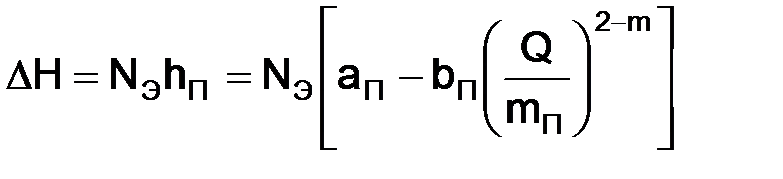 и
и ,
, , (1.36)
, (1.36) . (1.37)
. (1.37)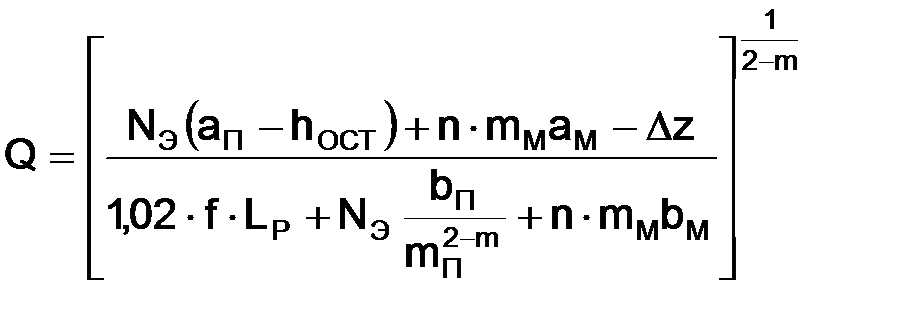 . (1.38)
. (1.38)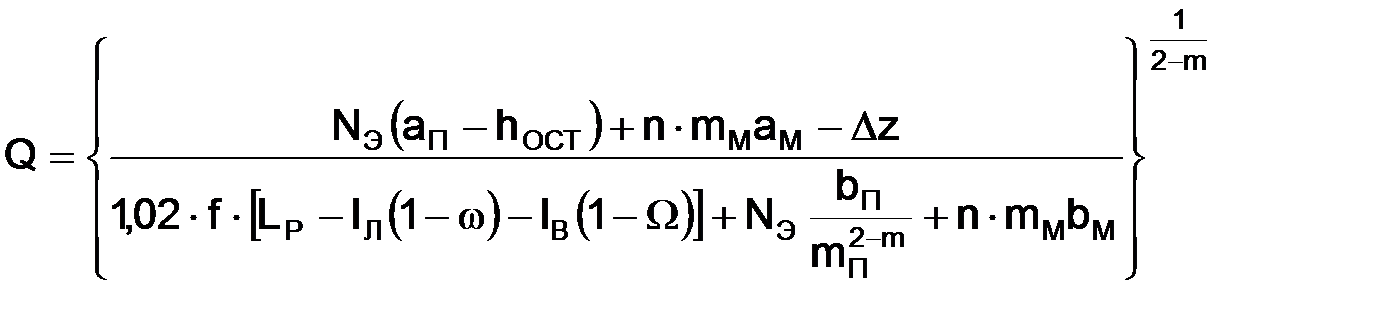 . (1.39)
. (1.39)
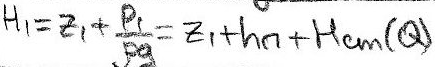
 - полн. напор на входе из НПС
- полн. напор на входе из НПС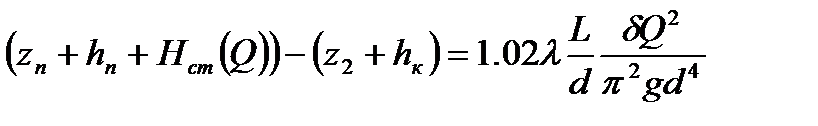
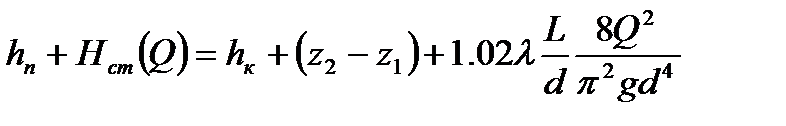
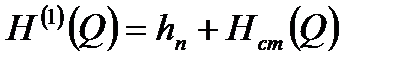 - гидравл. хар-тика НПС, а правая часть
- гидравл. хар-тика НПС, а правая часть 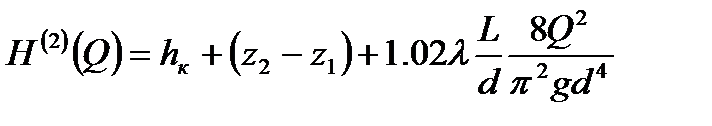 - гидравл. хар-ка участка трубопровода.
- гидравл. хар-ка участка трубопровода.

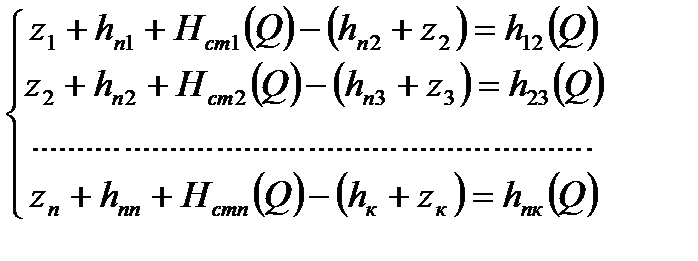
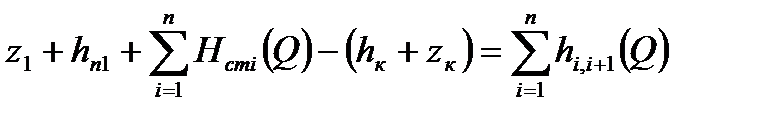
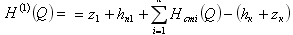 - суммар. гидрав. хар-ка всех НПС, а правая часть
- суммар. гидрав. хар-ка всех НПС, а правая часть 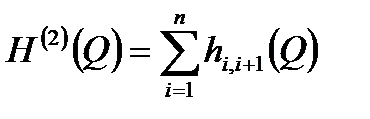 - сумм. гидравл. хар-ка всего т/п.
- сумм. гидравл. хар-ка всего т/п.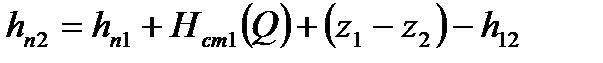 . Зная величину подпора на второй НПС, можно опр. давление на входе второй НПС
. Зная величину подпора на второй НПС, можно опр. давление на входе второй НПС  и давление на нагнетании второй НПС
и давление на нагнетании второй НПС 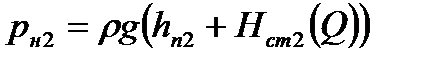 .
.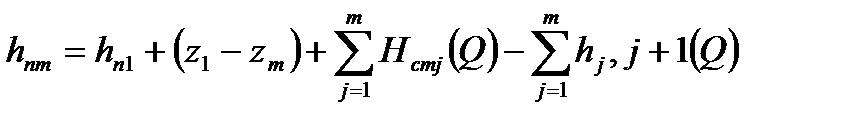
 и давление на нагнетат. линии m -ой НПС
и давление на нагнетат. линии m -ой НПС 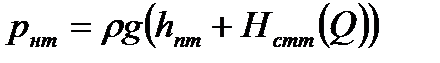

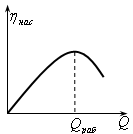
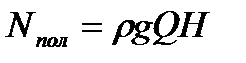 , где Q - подача насоса; H - дифф. напор, развиваемый насосом. [Nпол]=[Дж/с]=[Вт]
, где Q - подача насоса; H - дифф. напор, развиваемый насосом. [Nпол]=[Дж/с]=[Вт]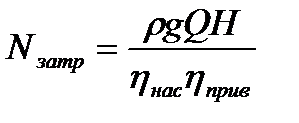 , где ηнас - КПД насоса, ≈80%; ηприв - КПД привода, ≈95%;
, где ηнас - КПД насоса, ≈80%; ηприв - КПД привода, ≈95%;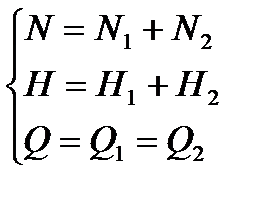 , →
, →