
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Растворимость солей, кислот и оснований в водеСодержание книги
Поиск на нашем сайте
Примечание. Н – нерастворимые; М – малорастворимые; Р – растворимые; «–» не существуют.
ХИМИЧЕСКАЯ ТЕРМОДИНАМИКА
Химическая термодинамика изучает законы обмена энергией макроскопических систем с окружающей средой, а также превращения одних форм энергии в другие внутри систем во время протекания в них физических и химических процессов. Законы термодинамики очень важны для химии, так как позволяют не только определять вид и величину энергии, выделяемой или поглощаемой в ходе химических реакций, но и предсказывать направление протекания реакций. Необходимо знать важнейшие понятия химической термодинамики. Термодинамическая система – макроскопическая часть окружающего мира, в которой протекают различные физические и химические процессы. Открытые системы обмениваются веществом и энергией с окружающей средой. Закрытые системы обмениваются энергией, но не обмениваются веществом. Замкнутые (изолированные) системы не обмениваются ни веществом, ни энергией с окружающей средой. Термодинамические переменные – макроскопические величины, описывающие состояние и свойства системы и ее окружения, которые могут изменяться при протекании различных процессов. Эти величины могут быть измерены или вычислены (масса m, объем V, давление P, температура Т, показатель преломления n, энергия E, плотность ρ, диэлектрическая проницаемость ε и т. п.). Термодинамические параметры – макроскопические величины, характеризующие систему или ее окружение и не изменяющиеся при протекании тех или иных процессов. Делятся на два типа: экстенсивные и интенсивные. Экстенсивные переменные зависят от числа частиц и, как правило, аддитивны (величина целого равна сумме величин частей): объём, масса, энергия и т. п. Интенсивные переменные напрямую не зависят от общего числа частиц: давление, температура, концентрация, диэлектрическая проницаемость и т. д. Фазы системы – однородные макроскопические части системы, имеющие поверхности раздела (лёд и вода, жидкость и её насыщенный пар в сосуде и т. п.). Компоненты системы – составные части системы, способные к независимому существованию. Состояния системы бывают равновесные и неравновесные. Состояние равновесно, если интенсивные переменные Р и Т не изменяются от точки к точке в системе, другие интенсивные переменные внутри каждой конкретной фазы также неизменны и испытывают скачок только на границах раздела фаз, при этом отсутствуют какие-либо перемещения макроскопических частей системы относительно друг друга. Состояние неравновесно, если в разных частях системы значения интенсивных параметров различны и имеются макроскопические перемещения внутри системы. Всякая макроскопическая система, предоставленная сама себе, стремится к состоянию равновесия. Функция термодинамических переменных F (P, V, T, …) системы называется ее функцией состояния, если ее значение зависит только от величин термодинамических переменных в данном конкретном равновесном состоянии системы и не зависит от предыдущих состояний системы. Внутренняя энергия системы – её важнейшая функция состояния. Полная энергия термодинамической системы в системе отсчёта, где термодинамическая система покоится как целое, называется внутренней энергией. Часто обозначается латинской буквой U,и ее величина определяется следующим образом:
где Первое начало (закон) термодинамики – закон сохранения энергии в приложении к термодинамическим системам. Рассмотрим для простоты некоторую закрытую систему. Поступление энергии в эту систему из её окружения может протекать двумя способами: 1 При контакте системы с окружающей средой без каких-либо перемещений ее макроскопических стенок. Такой способ называют теплообменом, а количество энергии, поступившей при этом, называют теплотой. 2 При перемещении макроскопических стенок системы. Количество энергии, переданное таким путем, называется работой. Отсюда следует уравнение (2.2):
Здесь DU – изменение внутренней энергии системы. Оно не зависит от пути процесса, если начальное и конечное состояния системы равновесны, так как U – функция состояния. Величина Q – количество энергии, поступившей в систему в процессе теплообмена, A – количество энергии, поступившей в систему за счет работы. В отличие от DU, величины Q и A зависят в общем случае от пути процесса, поэтому не следует говорить о количестве теплоты и работы в системе. В системе СИ размерности внутренней энергии, теплоты и работы одинаковы и выражаются в Дж. Правило знаков. В формуле (2.2) предполагается, что DU, Q и A > 0, когда энергия и теплота поступают в систему, работа совершается над системой. Уравнение (2.2) является математической записью первого начала термодинамики, или закона сохранения энергии для закрытой системы: изменение энергии закрытой системы равно подведенной к системе теплоте плюс совершенной над системой работе. Изохорный процесс (V = const). Как известно, при небольшом изменении объёма системы величина работы определяется формулой
Так как V = const, получаем уравнение (2.4):
Индекс «n»у теплоты Q означает, что процесс идёт при постоянном объёме. Из (2.4) видно, что теплота, полученная или отданная в изохорном процессе, не зависит от пути его протекания, а определяется только конечным и начальным равновесными состояниями системы. Изобарный процесс (P = const).
Индекс «р» у теплоты Q означает, что процесс идёт при постоянном давлении. Произведём замену переменных в первом слагаемом правой части, выразив величину P∆V через величину D(PV):
Функция состояния термодинамической системы H = U + PV называется энтальпией, или тепловой функцией (теплосодержанием) системы. Эта величина измеряется в джоулях. Её изменение – это энтальпия процесса.
Теплота, полученная или отданная в изобарном процессе, не зависит от пути его протекания, а определяется только конечным и начальным равновесными состояниями системы. Если уравнения (2.4) и (2.7) применить к произвольной химической реакции, протекающей до конца, то получим формулировку известного в термохимии закона Гесса: тепловой эффект химической реакции при постоянном объеме или постоянном давлении не зависит от пути ее протекания и последовательности ее стадий, а определяется только химическим составом и физическим состоянием конечных продуктов и исходных реагентов. При Q < 0 (теплота выделяется системой) реакция называется экзотермической, а при Q > 0 (теплота поглощается системой) – эндотермической. Следовательно, ∆U < 0, ∆H < 0 отвечает экзотермической реакции, а ∆U > 0, ∆H > 0 эндотермической реакции соответственно. Закон Гесса позволяет легко рассчитывать тепловые эффекты подавляющего большинства практически важных реакций, пользуясь накопленными экспериментальными данными для других реакций, которые сведены в специальные таблицы. Расчёты обычно ведут для изобарных процессов в стандартных условиях: давление равно 101 325 Па (1 физ. атмосфере, или 760 мм рт. ст.), температура равна 298,15 К (25 °С). При этом используется следствие из закона Гесса, согласно которому тепловой эффект химической реакции
где n i и n j – стехиометрические коэффициенты уравнения реакции для продуктов (индекс i) и исходных веществ (индекс j), Теплотой образования вещества (DH 0 ) называется тепловой эффект реакции образования 1 моля сложного вещества из простых веществ, устойчивых при стандартных условиях. Теплоты образования простых веществ зависят от агрегатного состояния вещества, и для их устойчивых состояний в стандартных условиях эти теплоты приняты равными нулю. Стандартные теплоты образования ряда сложных веществ из простых веществ приведены в табл. 2.1. Тепловой эффект химической реакции можно также вычислить, используя второе следствие из закона Гесса: тепловой эффект химической реакции
где Теплотой сгорания вещества (DHсгор.) называется тепловой эффект реакции окисления 1 моля вещества кислородом с образованием высших (устойчивых) оксидов. Для органических соединений теплотой сгорания называется тепловой эффект реакции полного сгорания 1 моля данного органического вещества с образованием CO2 и H2O. Стандартные теплоты сгорания приведены в табл. 2.2. Обратите внимание на то, что теплоты сгорания высших оксидов (H2O, CO2 и т. п.) также приняты равными нулю. Пример 1. Вычислите стандартную теплоту образования бензола на основании термохимического уравнения реакции его сгорания: C6H6 (ж) + Решение: По следствию из закона Гесса:
Выразим из уравнения (1) теплоту образования бензола:
и подставим численные значения из табл. 2.1:
Пример 2. Рассчитайте количество тепла, которое выделяется при сгорании одного кубометра пропана при нормальных условиях. Решение Запишем термохимическое уравнение реакции сгорания: C3H8 + 5O2 = 3CO2 + 4H2O(г); ∆ Hхр Применяя к исходному уравнению следствие из закона Гесса, получаем:
Подставим табличные значения теплот образования, учитывая, что теплоты образования простых веществ приняты равными нулю: ∆ Hхр = 3(–393,51) + 4(–241,83) – (–103,92) = –2043,93 кДж/моль. Найденное количество тепла выделяется при сгорании одного моля пропана. Напомним, что 1 моль газа при нормальных условиях занимает объем VM = 22,4 л/моль. По условию задачи сгорает
Количество тепла, выделяемого при сгорании 1 м3 пропана, равно:
Надо подчеркнуть, что следствие из закона Гесса широко используется также для расчета изменения энтропии и изобарных потенциалов при химических реакциях.
Таблица 2.1 Термодинамические функции D Нобр (кДж/моль) и S 0 (Дж/ моль∙К) некоторых веществ при стандартных условиях
Таблица 2.2 Стандартные теплоты сгорания
Все процессы, протекающие в термодинамических системах, можно разделить на два класса – самопроизвольные и несамопроизвольные. Самопроизвольные процессы всегда протекают необратимо, а несамопроизвольные могут быть обратимыми. Обратимым называют такой процесс, который можно в любой момент заставить протекать в обратном направлении через те же стадии, по которым он протекал в прямом направлении. Обратимые процессы никогда не протекают самопроизвольно, они всегда требуют внешних воздействий (совершения работы и подведения или отведения тепла). Самопроизвольные процессы в термодинамических системах протекают самопроизвольно, без каких-либо внешних воздействий. Вода сама течёт вниз по склону, теплота переходит от нагретых тел к холодным, а не наоборот. Самопроизвольные процессы, протекая в одном направлении, никогда затем не идут в обратном направлении самопроизвольно, они однонаправленны. Первое начало термодинамики ничего не говорит о направлении процессов, протекающих в природе и технике. Второе начало (закон) термодинамики даёт такие предсказания. Математическое выражение второго начала термодинамики осуществляется с помощью введения специальной аддитивной функции состояния, которая называется энтропией, малое изменение которой dS по определению равно:
где Т – абсолютная температура системы. Размерность энтропии – Дж/К. Постулируем основное неравенство, являющееся одним из математических выражений второго начала термодинамики:
Величина Если система замкнута (изолирована), она не обменивается энергией с окружающей средой и неравенство (2.11) приобретает вид (2.12)
Неравенство (2.12) называется законом возрастания энтропии, являющимся наиболее общей формулировкой второго начала термодинамики: энтропия изолированной системы при любых протекающих в ней процессах никогда не убывает, она либо растёт, либо остаётся постоянной. Последнее реализуется, когда система пребывает в состоянии равновесия. При протекании самопроизвольного процесса в замкнутой системе энтропия всегда растёт. Очевидно, энтропия в системе СИ измеряется в Дж/К. Статистический смысл энтропии. Макроскопическое состояние термодинамической системы задаётся её макроскопическими переменными, такими как объём, давление, температура, концентрации и другие. Если для двух состояний системы эти переменные одинаковы, то и состояния одинаковы. Однако при микроскопическом рассмотрении системы легко обнаруживается, что данному макроскопическому состоянию системы соответствует весьма большое число неотличимых с макроскопической точки зрения микроскопических состояний. Так, например, данной величине давления газа на стенку сосуда соответствуют в разные моменты времени разные положения различных молекул по отношению друг к другу и удары молекул о стенку сосуда. Можно говорить о неком, при этом весьма большом, среднем числе W микросостояний системы, соответствующих данному макроскопическому состоянию. Больцман показал, что абсолютная энтропия системы связана с логарифмом среднего числа микросостояний системы W:
где k – константа Больцмана, k = 1,381·10-23 Дж/К. Из формулы (2.13) видно, что энтропия – мера статистического беспорядка в системе. При переходе вещества от кристаллического состояния к жидкому, а затем от жидкости к газу, его энтропия растёт, значит, растёт и число микросостояний, последовательно отвечающих каждому из этих макроскопических состояний. Учитывая статистический смысл энтропии, второе начало термодинамики можно сформулировать следующим образом: изолированная система, находящаяся в неравновесном состоянии, стремится к состоянию равновесия, которому отвечает наибольшее среднее число микросостояний системы. Для того чтобы выбрать начало отсчета абсолютной энтропии термодинамической системы, используют третье начало термодинамики, которое формулируется согласно Планку следующим образом: энтропия всех индивидуальных веществ, существующих в виде идеальных кристаллов при температуре абсолютного нуля, равна нулю. Предположим, что температура одного моля индивидуального вещества при постоянном давлении, например стандартном, увеличивается от абсолютного нуля (где вещество находится в состоянии идеального кристалла) до температуры Т, где вещество находится в газообразном состоянии. Тогда осуществляются следующие процессы нагревания вещества и его переходов из одних агрегатных состояний в другие.
Эти процессы могут протекать обратимо. Энтропия в конечном состоянии с температурой Т равна сумме изменений энтропии, произошедших на всех предыдущих этапах. Определенная таким образом величина S(T) есть абсолютная энтропия одного моля индивидуального вещества при температуре T и давлении P, выражается в Дж/(К·моль). В термохимических таблицах обычно приводятся стандартные мольные абсолютные энтропии индивидуальных веществ S 0, определяемые для стандартных условий (Т = 298,15 К, Р = 101325 Па) (см. табл. 2.1). Поскольку энтропия – аддитивная функция состояния, расчет изменения энтропии химической реакции
где В уравнении (2.14), в отличие от подсчета величины В случае закрытой системы постоянного состава, которая может совершать только работу расширения, можно объединить I и II начала термодинамики для обратимого процесса. Для этого в уравнение (2.2) подставим величину
Это уравнение часто называют фундаментальным уравнением для закрытой системы постоянного состава. Приведем некоторые важные положения термодинамики без доказательства. Вводится функция состояния G термодинамической системы, определяемая равенством
где ∆G – изменение изобарно-изотермического потенциала или потенциала Гиббса при протекании некоторого процесса в термодинамической системе. Критерий протекания самопроизвольных процессов: процесс в термодинамической системе протекает самопроизвольно при постоянных давлении и температуре, если изменение изобарного потенциала в системе меньше нуля (∆G < 0). Если ∆G = 0, то система находится в состоянии равновесия;
Величина ∆G 0 вычисляется так, как если бы химическая реакция протекала до конца. Величины ∆Н 0 и ∆S 0 вычисляются по формулам (2.8) и (2.14). Важность величины ∆G 0 заключается в том, что она связана с величиной константы химического равновесия K выражением (2.18):
Отметим, что в выражении (2.18) константа равновесия K безразмерна. Эта величина выражается или через парциальные давления реагентов, деленные на стандартное давление, или через концентрации реагентов, деленные на стандартные концентрации (например, 1 моль/л). Выражение (2.18), если вычислена величина ∆G 0для конкретной реакции, позволяет судить о величине константы равновесия и о том, в сторону какой реакции сдвинуто равновесие (K < 1 – в сторону исходных реагентов, K > 1 – в сторону продуктов реакции, K = 1 – равновесие примерно посередине).
Пример 3. Рассмотрите протекание реакции разложения перхлората калия в закрытой системе:
4KClO4(тв) = 2KClO3(тв) + 2KCl(г) + 5O2(г); ∆ H0хр = 50 кДж.
Решение Вычислим величину D G 0 этой реакции. Величина ∆ H 0 хр нам уже известна из термохимического уравнения реакции. Вычислим величину
Подставим стандартные энтропии участников реакции из таблицы 2.1: ∆ Sхр = 2×143 + 2×83 + 5×205 - 4×151 = 873 Дж. Следовательно, величина DG0 равна: D G 0 = ∆ H 0 – T ∆ S 0 = 50000 – 873∙298 = –210154 Дж. Рассчитаем величину константы равновесия химической реакции при стандартных условиях, выразив её из уравнения (2.18):
Как видно из расчета, равновесие реакции разложения перхлората практически полностью сдвинуто вправо. Очевидно, что самопроизвольное разложение перхлората возможно в закрытой системе. Однако термодинамика ничего не говорит о том, с какой скоростью будет протекать реакция. Найдем температуру T, при которой равновесие реакции разложения перхлората будет находиться примерно посередине между прямой и обратной реакциями. Этому будет соответствовать величина DGреакции = 0, откуда следует, что величина константы равновесия равна единице (формула (2.18)). Примем, что величины DH 0 и DS 0 практически не изменяются с изменением температуры. Тогда будем иметь ∆G 0 = ∆H 0– T∆S0 = 0 и
Пример 4. Вычислите значения стандартных изобарных потенциалов обратимой реакции: 2NO(г) + O2(г) Á 2NO2(г)
в температурном интервале 800–1100 К, через каждые 100 К, считая, что DH 0 и DS 0 не зависят от температуры. Постройте график ∆G0 = f(T) и сделайте вывод о направлении смещения равновесия реакции при разных температурах. Решение Запишем уравнение реакции в стандартном виде:
NO(г) +
По закону Гесса с помощью таблицы 2.1 найдем стандартное изменение энтальпии при этой реакции:
∆H0хр =
(поскольку кислород – простое вещество, то ∆ H 0 обр = 0). Теперь оценим изменение энтропии этой реакции. Качественная оценка может быть сделана на основе сопоставления числа молей газообразных конечных продуктов и исходных веществ: Проверим этот вывод путем расчета, используя данные таблицы 2.1.
Знак выражения ∆ S 0 < 0 свидетельствует о том, что беспорядок в изолированной системе при протекании прямой реакции до конца уменьшается. Найденные стандартные изменения энтальпии и энтропии имеют одинаковый знак, что свидетельствует о существовании такой температуры, при которой ∆G = 0, и равновесие химической реакции находится посередине. Подставим числовые значения изменений стандартных энтропии и энтальпии химической реакции в уравнение (2.17) и вычислим значение ∆G 0как функцию температуры: ∆ G 800 = +0,8; ∆ G 900 = +8,15; ∆ G 1000 = +15,5; ∆ G 1100 = +22,85 кДж/моль На основании этих данных строим график ∆ G = f (Т):
Рис. 2.1. Зависимость изменения изобарного потенциала
Из рис. 2.1 видно, что прямая линия на этом графике отражает совокупность равновесных состояний для обратимой реакции. Линия выражает множество равновесных состояний в заданном интервале температур. Роль температурного коэффициента для этой линии играет стандартная энтропия реакции ∆S 0, взятая с обратным знаком: чем больше величина ∆S 0, тем сильнее выражена зависимость ∆G = f(T). Точка пересечения с осью температуры характеризует температуру Величина стандартного изобарного потенциала позволяет оценить устойчивость, реакционную способность молекул и, соответственно, многие их химические свойства. Сопоставляя величины ∆G 0 для ряда веществ, можно сделать вывод о характере кислотно-основных и окислительно-восстановительных свойств и др. Задачи
21 Разложение бихромата аммония может быть описано следующим уравнением: (NH4)2Cr2O7(Г) = Cr2O3(Т) + N2(Г) + 4H2O(Г). Разложение сопровождается выделением q = 1344 кДж тепла. Сколько литров азота при этом образуется? Условия нормальные. Ответ: V = 100 л.
22– |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 328; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.224.105 (0.01 с.) |

 I–
I–
 Соли и гидроксиды Na
Соли и гидроксиды Na  , K
, K 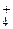 растворимы.
растворимы.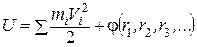 ,
,
 – кинетическая энергия всех частиц термодинамической системы,
– кинетическая энергия всех частиц термодинамической системы, 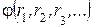 – потенциальная энергия их взаимодействия. Эту функцию невозможно не только детально записать, но и вычислить для конкретной системы. Однако экспериментально или теоретически легко определить величину изменения этой функции при переходе системы из одного состояния в другое.
– потенциальная энергия их взаимодействия. Эту функцию невозможно не только детально записать, но и вычислить для конкретной системы. Однако экспериментально или теоретически легко определить величину изменения этой функции при переходе системы из одного состояния в другое.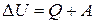 .
.
 ∆U = –P∆V + Qp.
∆U = –P∆V + Qp.

 равен
равен ,
,
 и
и  – мольные энтальпии (теплоты) образования продуктов реакции и исходных веществ соответственно. Верхний индекс 0 повсеместно указывает на стандартные условия.
– мольные энтальпии (теплоты) образования продуктов реакции и исходных веществ соответственно. Верхний индекс 0 повсеместно указывает на стандартные условия.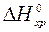 равен
равен
 и
и  – мольные энтальпии (теплоты) сгорания продуктов реакции и исходных веществ соответственно.
– мольные энтальпии (теплоты) сгорания продуктов реакции и исходных веществ соответственно. O2 = 6CO2 (г) + 3H2O(г); D Hхр = –3133 кДж/моль.
O2 = 6CO2 (г) + 3H2O(г); D Hхр = –3133 кДж/моль.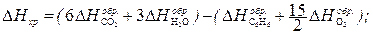 (1)
(1)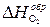 = 0, т. к. это простое вещество.
= 0, т. к. это простое вещество. .
.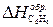 = 6 (-393) + 3 (-242) + 3133 = 49 кДж/моль.
= 6 (-393) + 3 (-242) + 3133 = 49 кДж/моль.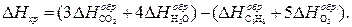
 , т. е.:
, т. е.:
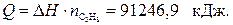


 C6H5NH2(ж)
C6H5NH2(ж)
 , кДж/моль
, кДж/моль
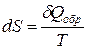 ,
,

 называется приведённой теплотой. Изменение энтропии при протекании процесса в системе больше или равно сумме приведённых теплот в этом процессе.
называется приведённой теплотой. Изменение энтропии при протекании процесса в системе больше или равно сумме приведённых теплот в этом процессе.

 , протекающей до конца, проводится аналогично расчету энтальпии химической реакции
, протекающей до конца, проводится аналогично расчету энтальпии химической реакции  :
: ,
,
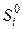 ,
,  – абсолютные мольные энтропии продуктов реакции и исходных веществ соответственно в Дж/(К·моль).
– абсолютные мольные энтропии продуктов реакции и исходных веществ соответственно в Дж/(К·моль).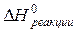 по (2.8), следует учитывать стандартные мольные энтропии как сложных, так и простых веществ. Простым веществам невозможно приписать нулевые значения стандартных энтропий.
по (2.8), следует учитывать стандартные мольные энтропии как сложных, так и простых веществ. Простым веществам невозможно приписать нулевые значения стандартных энтропий. из уравнения (2.9) и получим (2.15):
из уравнения (2.9) и получим (2.15):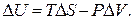
 . Функция G называется изобарно-изотермическим потенциалом, или просто изобарным потенциалом, или потенциалом Гиббса, измеряется в джоулях. В изобарно-изотермических условиях для закрытой термодинамической системы имеется важный критерий самопроизвольности протекания процессов:
. Функция G называется изобарно-изотермическим потенциалом, или просто изобарным потенциалом, или потенциалом Гиббса, измеряется в джоулях. В изобарно-изотермических условиях для закрытой термодинамической системы имеется важный критерий самопроизвольности протекания процессов: . Согласно уравнению (2.16) и уравнению химической реакции величину
. Согласно уравнению (2.16) и уравнению химической реакции величину 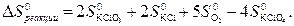
 ,
, .
. .
.
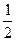 O2(г) Á NO2(г); ∆ Hхр .
O2(г) Á NO2(г); ∆ Hхр . –
–  = 33 – 91 = –58 кДж/моль
= 33 – 91 = –58 кДж/моль = 240 – 211 –
= 240 – 211 – 



