
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Конструирование покрытий по стрельчатым аркамСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ АРХИТЕКТУРНО-СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ
Г.Н. ШМЕЛЕВ КРУГОВАЯ И СТРЕЛЬЧАТАЯ АРКА Рекомендовано Учебно-методическим объединением вузов РФ по образованию в области строительства в качестве учебного пособия для студентов, обучающихся по направлению 270100 «Строительство»
Казань, 2015 год УДК 694 ББК 38.55 Ш 72
Шмелёв Г. Н. Ш 72 Круговые и стрельчатые арки: Учебное пособие. Казань: КГАСУ, 2015. – 117 с.
В учебном пособии приведены основы расчёта и конструирования круговых и стрельчатых арок, справочные данные и графическая часть проектов. Выполнение расчётов вручную и в программном комплексе позволит студентам сравнить результаты двух методов расчета. Предназначено для студентов, обучающихся по направлению «Строительство».
Рецензенты: Главный инженер «Казанский ГИПРОНИИАВИАПРОМ» Никитин Г.П. Доцент кафедры конструкций из дерева, древесных композитов и пластмасс ННГАСУ Крицин А.В.
УДК 694 ББК 38.55
© Казанский государственный архитектурно-строительный университет, 2015 © Шмелев Г.Н., 2015 Содержание
Введение
Повышение производительности труда, в том числе в учебном процессе, невозможно без интенсивного применения информационных технологий, особенно на трудоемких этапах; статических расчетов, оформлении чертежей, пояснительной записки и т.д. Активному освоению традиционных и компьютерных технологий расчета и проектирования круговых и стрельчатых деревянных арок будет способствовать и разработанное учебное пособие. Разработанное пособие планируется использовать по курсу «Конструкции из дерева и пластмасс» на практических занятиях, в курсовой работе, которая включает обе эти схемы и дипломном проектировании по направлению «Строительство». Пособие позволяет студентам сравнивать результаты расчета, выполненные традиционно и на ПК «Лира». Приведена пошаговая технология расчета арок в наиболее используемом в проектных организациях ПК. В приложении приведены необходимые для расчета справочные данные и примеры выполнения графической части проекта по обеим схемам.
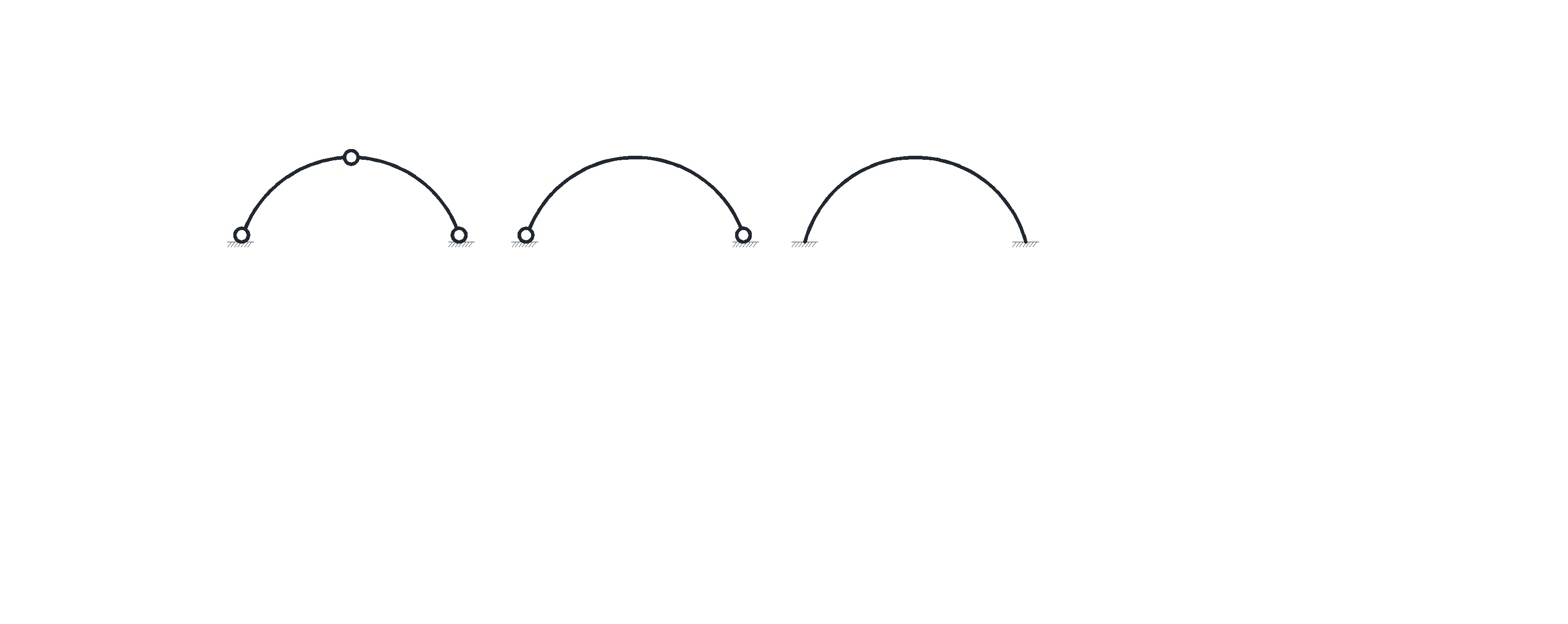
Общие сведения об арках Виды и область применения Деревянные арки широко применяются в качестве основных несущих конструкций зданий различного назначения: сельскохозяйственные, гражданские и общественные пролетом от 12 м до 70 м. За рубежом арки из дерева применяют при пролетах до 100 м и более. По статической схеме арки разделяют на трехшарнирные, двухшарнирные без ключевого шарнира и бесшарнирные.
Рис. 1.1. Статические схемы арок
По схеме опирания их делят на арки без затяжек, распор которых передается на опоры, и арки с затяжками, воспринимающими распор, который уже на опоры не передается.
Рис. 1.2. Арки с затяжками и без затяжек
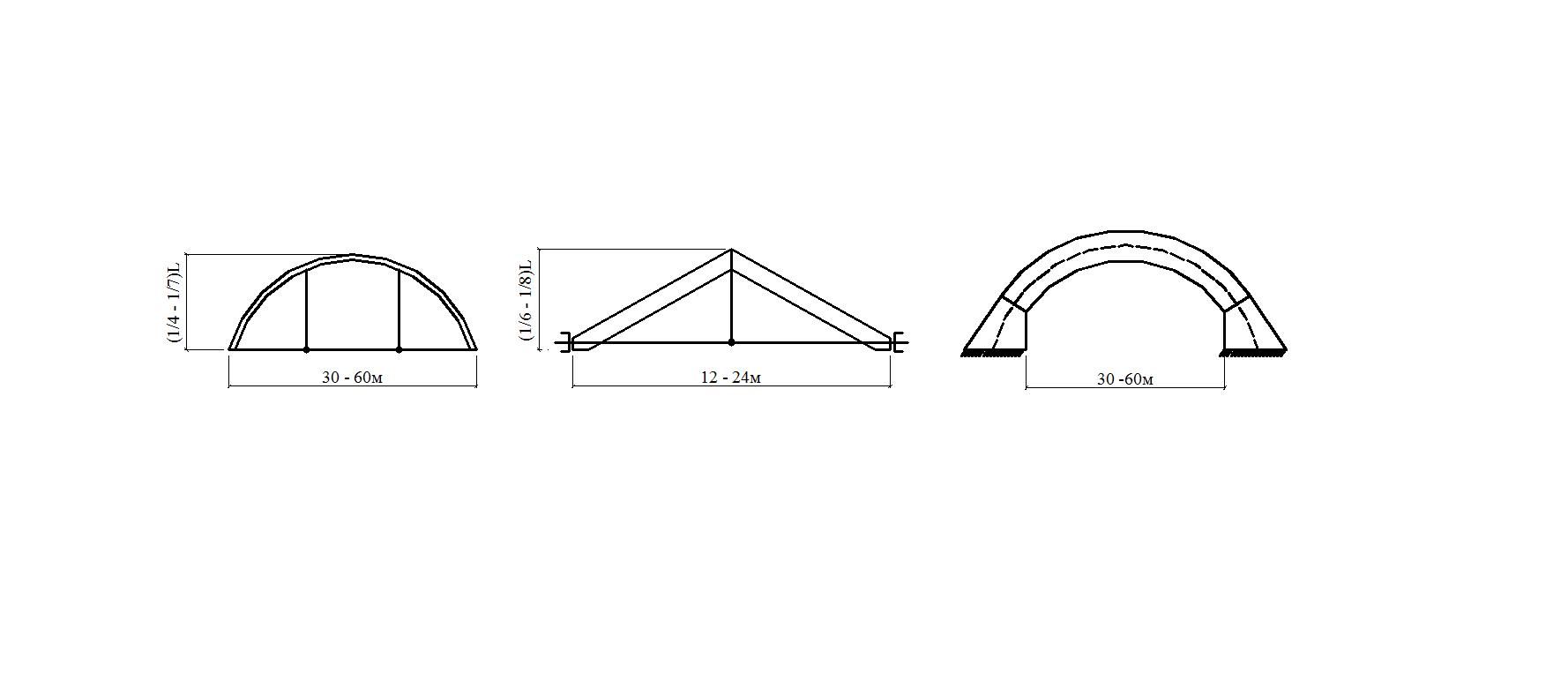
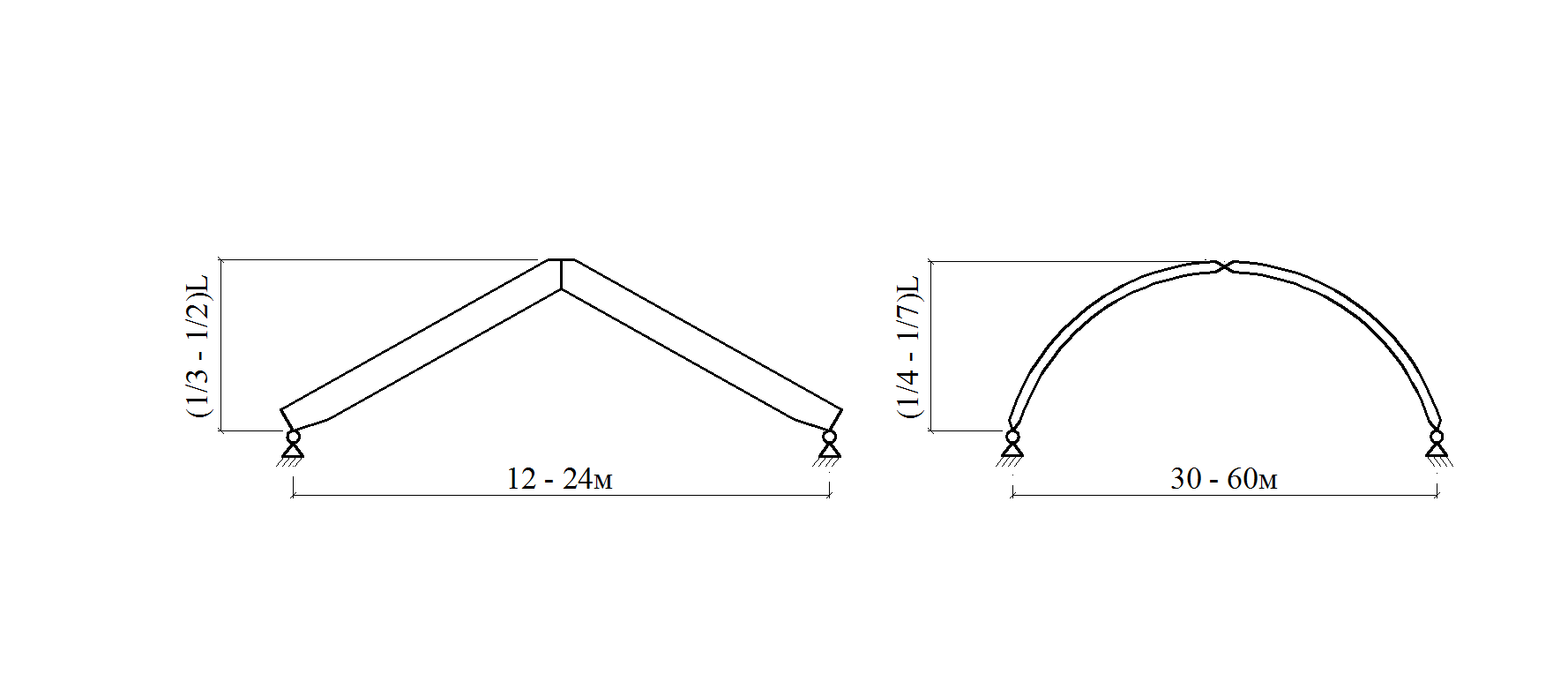
Рис. 1.3. Формы арок а) треугольная; б) круговая; в) стрельчатая; г) многоугольные
По конструкции арки делятся: - цельные; клееные; из ферм.
Рис. 1.4. Арки из ферм
Трехшарнирные арки являются наиболее простыми и распространенными. Усилия в них не зависят от деформаций опор и затяжек. Коньковый стык простой. Двухшарнирные арки применяют в отдельных случаях при сегментной ферме и клееных конструкциях. Они не имеют преимуществ по сравнению с трехшарнирными, но позволяют получить некоторую экономию, когда возможна транспортировка целых элементов. Арки без затяжек являются наиболее простыми, состоят только из двух одинаковых полуарок. Такие арки применяют в зданиях значительной высоты, как правило, без вертикальных стеновых ограждений: спортивные, зрелищные, складские помещения. Арки с затяжками применяют в покрытиях общего типа в том же качестве, что балки и фермы, и опирают на стены или колонны. Арки из клееных элементов заводского изготовления имеют наиболее широкую область применения, поскольку их форма, размеры и несущая способность могут отвечать требованиям сооружения самого различного назначения. Арки из целых элементов построечного изготовления могут найти эффективное применение, однако их форма, пролеты и несущая способность ограничена сортаментом стройматериалов. Дощатоклееные арки, склеенные из досок плашмя в условиях заводского изготовления, получили наибольшее распространение (L=12 – 16 м).
Треугольные клееные арки Они имеют трехшарнирную схему ( Треугольные арки отличаются простотой изготовления, не требуют гнутья досок, однако они имеют повышенный расход древесины и значительные пролетные моменты. Полуарки крепятся в углах с эксцентриситетом, позволяющим уменьшить моменты от вертикальных сил.
Сегментные клееные арки Они могут иметь трехшарнирную и двухшарнирную схемы. При малых пролетах изгибающие моменты в таких арках значительно меньше, чем в треугольных, а сосредоточенные нагрузки, вызывающие большие моменты, к ним, как правило, не прикладываются. Сечение поясов при небольших пролетах принимаются также до 17 см без поперечных стыков. При
Стрельчатые клееные арки Они имеют трехшарнирную схему и сегментное очертание полуарок. Применяют, как правило, без затяжек при Стрельчатые клееные арки применяют при действии распределенных и сосредоточенных нагрузок в зоне ключевого узла от подвесного оборудования. Пятиугольные арки имеют те же параметры что и стрельчатые. Форма и величина усилий в сечениях зависит от соотношения распределенной и сосредоточенной нагрузок. Чем больше относительная величина сосредоточенной нагрузки в зоне ключа, тем ближе форма оси арки должна приближаться к треугольной, при которой от этой нагрузки не возникает изгибающих моментов. Чем больше величина распределенных нагрузок, тем больше форма арки должна приближаться к параболической, при которой изгибающие моменты от них минимальны. Определяется оптимальное очертание.
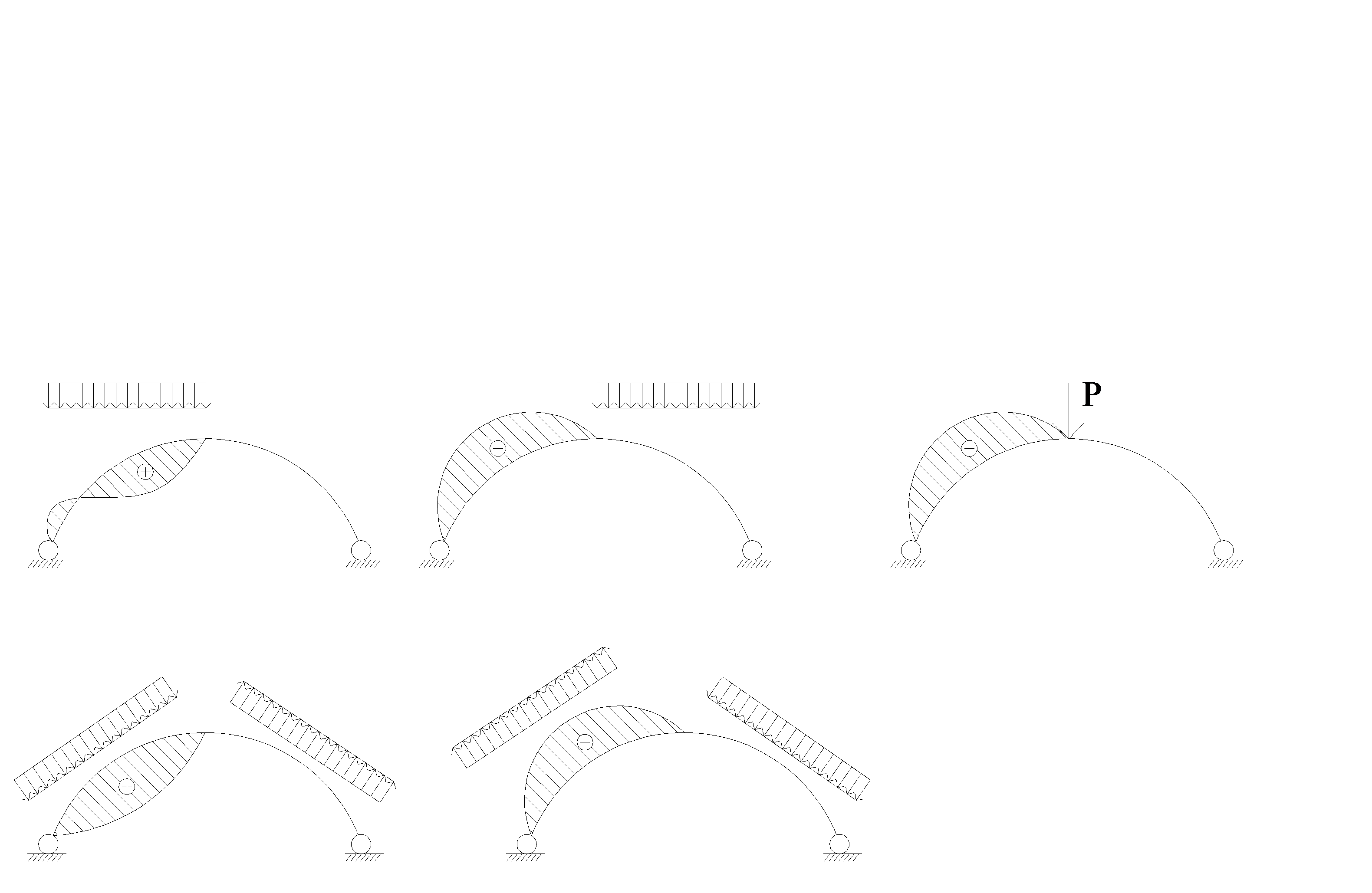
Рис. 1.5. Эпюры моментов в арке от: а) нагрузки на левой половине; б) нагрузки на правой половине; г) сосредоточенной; д) ветер слева; г) ветер справа.
В нашей стране имеется многочисленный успешный опыт применения большепролетных клееных стрельчатых арок в покрытиях складов комбинатов удобрений. L=45м; h=22.5м; радиус полуарок 31м. Оборудование располагается в зоне конькового узла. Полуарки имеют сечение 35 Пятиугольные клееные арки Они выполняются без затяжек. Полуарки состоят из двух сомкнутых прямолинейных участков. В местах переломов осей они имеют гнутые участки, создаваемые в процессе склеивания, или соединяются на угловое зубчатое соединение. Основным преимуществом является то, что покрытие по ним состоит из плоских поверхностей, удобных для устройства кровли из панелей, шифера и профнастила. Арки из целых элементов Они могут быть только треугольной формы и с затяжкой. Пролет до 12 м. Шаг стропил – 3 м. Они выполняются из спаренных досок с затяжкой из одной доски. Сквозные арки Они находили некоторое применение в большепролетных покрытиях. Полуарки представляют собой сегментные дощатые фермы с пониженной высотой 1) Геометрический расчет арки заключается в определении всех необходимых для статического расчета углов наклона и их геометрических функций. Для симметричных схем обычно рассматривают левую половину схемы. Рассматривать удобно в прямоугольной системе координат. Основными исходными величинами являются 2) Статический расчет арок производится в следующем порядке: - определяют действующие на арку нагрузки; - вычисляют опорные реакции: - R – вертикальную, H – горизонтальную; - M; N; Q; - подбирают сечение арки: - верхнего и нижнего поясов; - проверяют действующие напряжения - рассчитывают узловые соединения. Расчет деревянных арок Нагрузки от собственной массы определяются по формулам или по аналогам. Для сегментных арок S принимается в зависимости от H, l, L. Криволинейные эпюры разрешается заменять на прямолинейные и нормальные к хорде арок. В треугольных арках S зависит от угла наклона и отношения
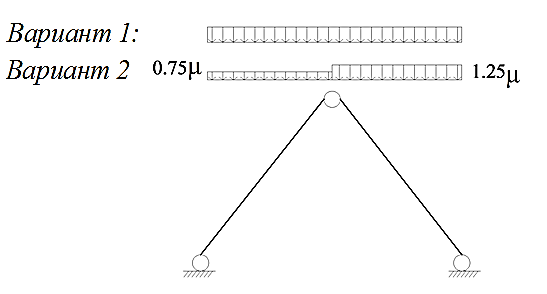
Треугольная арка При Вариант №1: Вариант №2:
Рис. 1.7. Снеговая нагрузка на треугольную арку
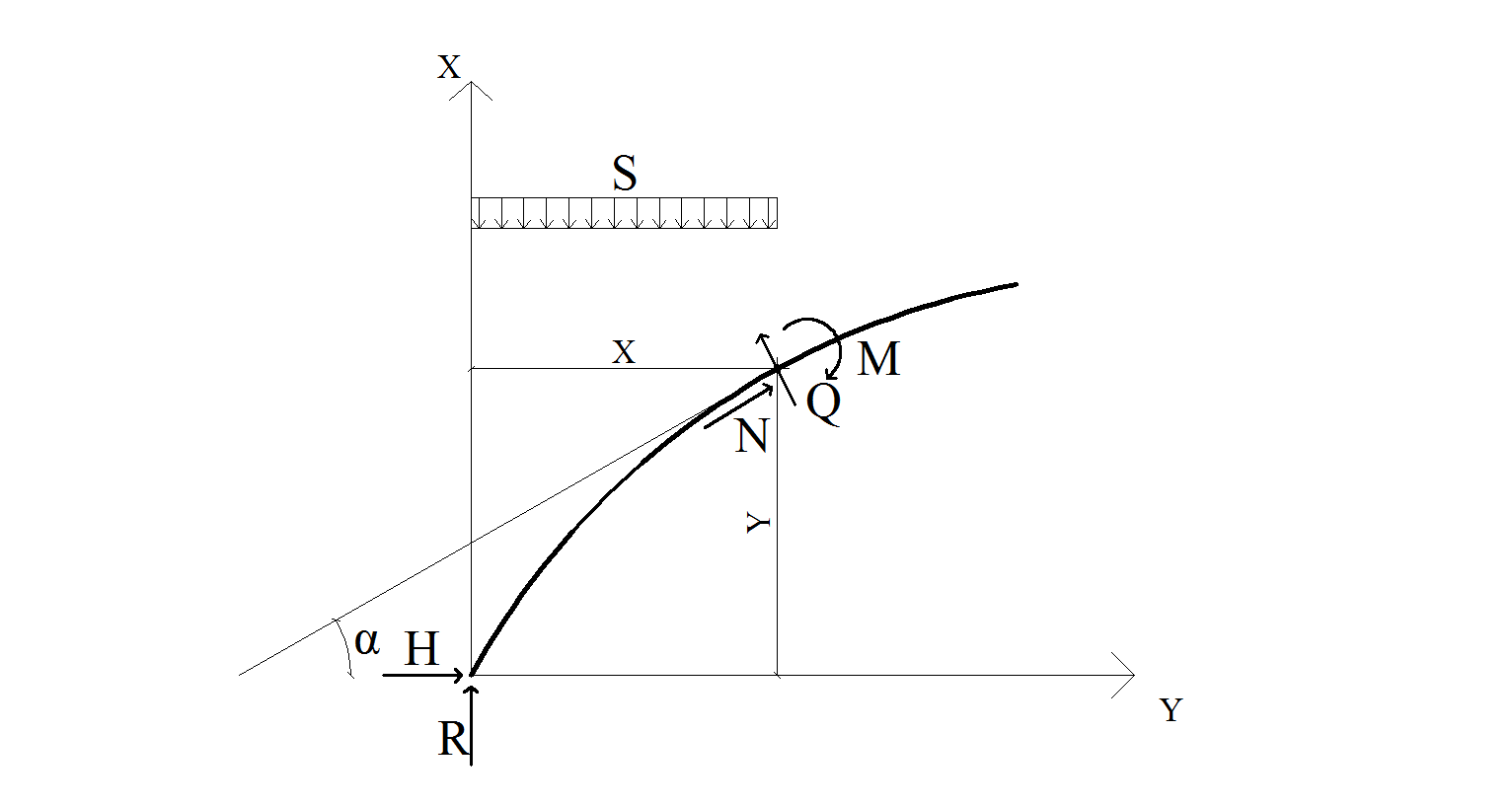
Определение усилий M, N, Q в выбранных сечениях
Рис. 1.8. К определению M, N, Q в сечениях арки Схема работы
Определенные усилия от рассматриваемых нагрузок заносят в таблицы и производят сочетания нагрузок. Максимальный изгибающий момент возникает обычно в сечениях близ четверти пролета арки (середины полуарки). Наибольшие продольные и поперечные силы возникают в сечениях арок в опорном и коньковом узлах. В треугольных арках моменты определяют с учетом эксцентриситета «е» крепления полуарок в опорном и коньковом узлах: Верхние пояса арок рассчитываются на сжатие с изгибом и скалывание, а нижние – на растяжение. Подбор сечения можно производить в следующем порядке: 1. Задаться шириной прямоугольного сечения, в начале b=14-17 см в одну доску. 2. Определить требуемую высоту сечения:
0.8 – коэффициент, учитывающий влияние продольной силы «N». Проверка нормальных напряжений:
N можно принять в коньке сегментной арки и в четверти стрельчатой и треугольной арок.
Расчет на устойчивость плоской формы верхнего пояса производят с учетом закрепления их распорками и плитами (прогонами). При действии отрицательных моментов верхняя зона растянута, а нижняя сжата и не закреплена. Необходим расчет, а при необеспечении устойчивости – дополнительные связи (распорки). Расчет узлов арок: 1) Опорный узел арок без затяжки Он проверяется на смятие по формуле при направлении волокон под углом
Рис. 1.9. Опорный узел сегментной арки
Рис. 1.10. Опорный узел треугольной арки
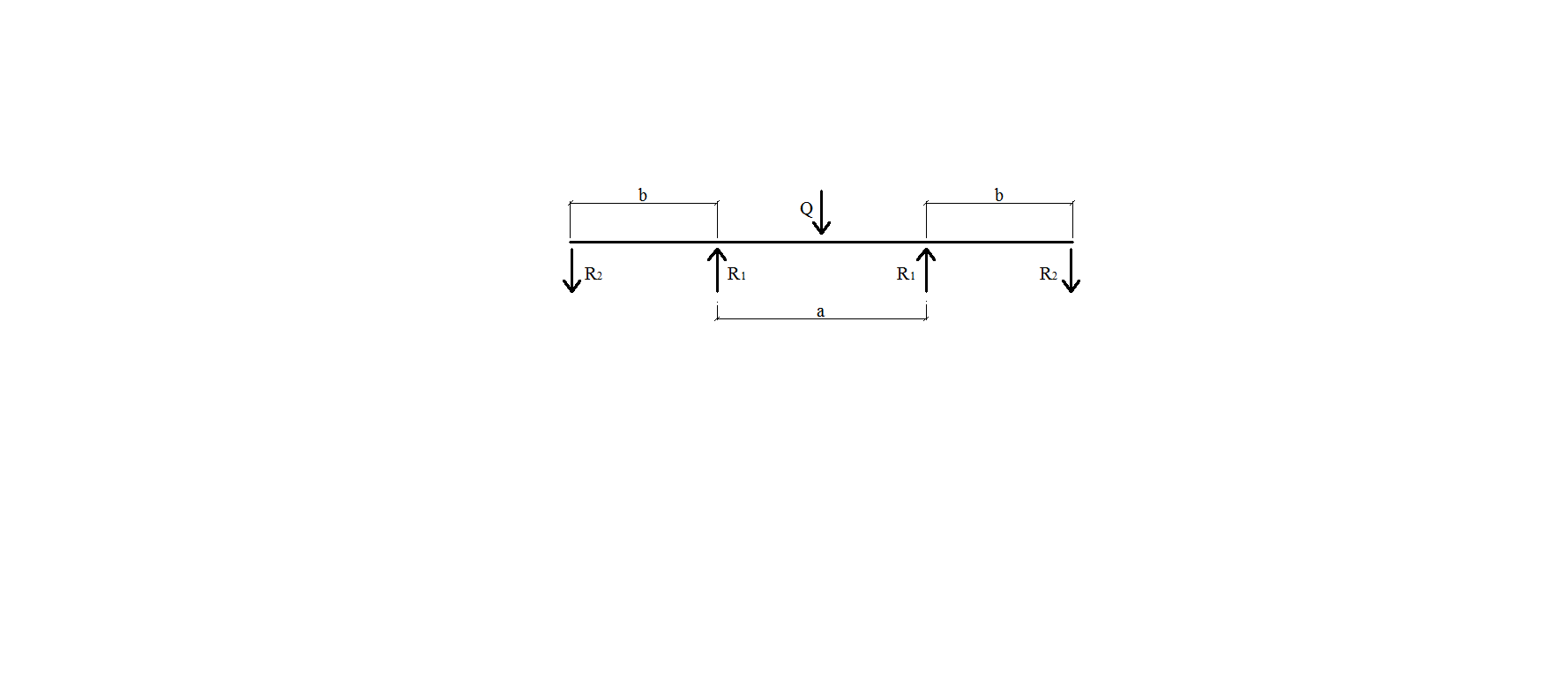
Число крепления концов сегментной и стрельчатой арок к боковым фасонкам башмака определяется по величине поперечной силы как для двусрезных нагельных соединений. Опорный лист башмака работает на изгиб как балка на упругом основании (см. схему расчета). Цилиндр опорной конструкции проверяется на цилиндрическое смятие по толщинам опорных ребер. 2) Опорный узел арок с затяжкой
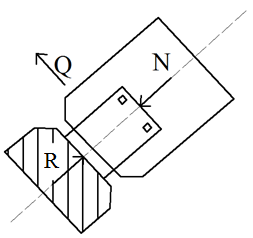
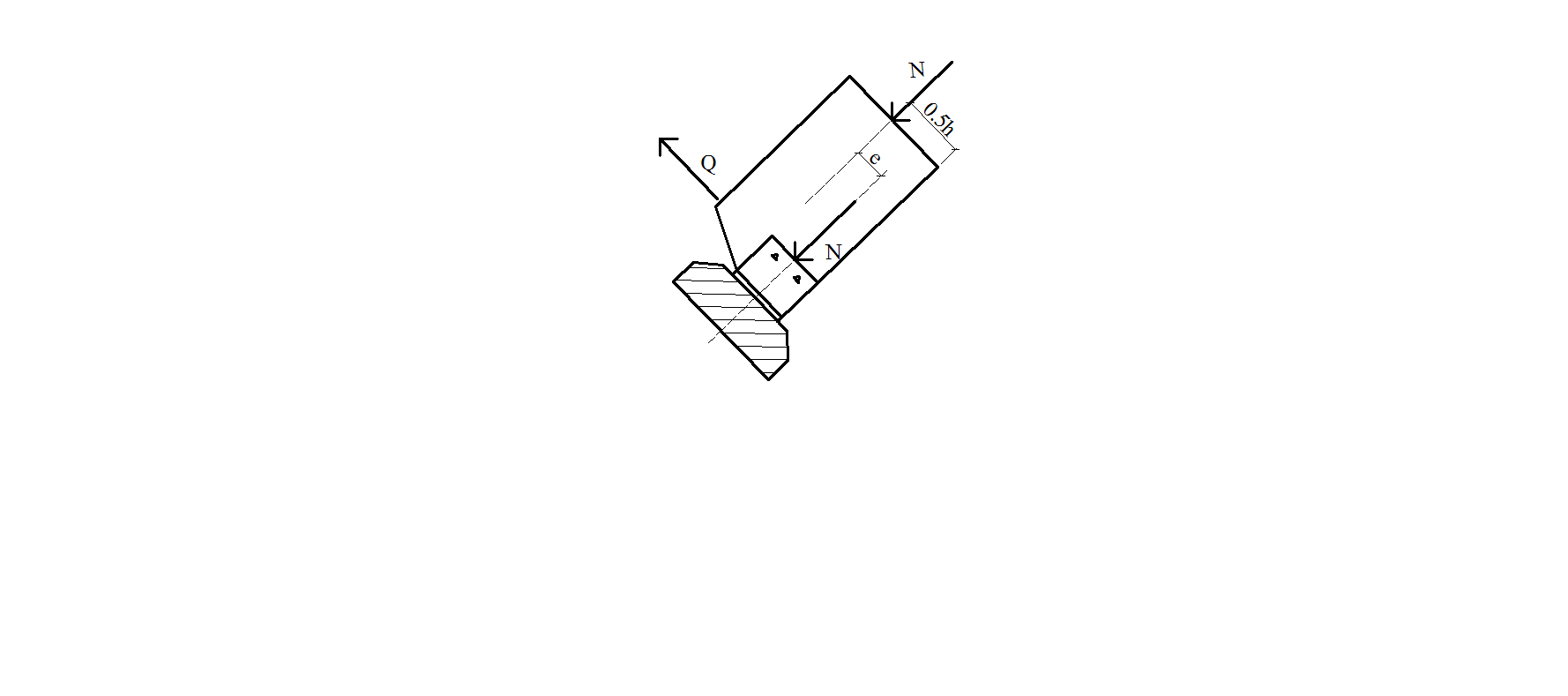
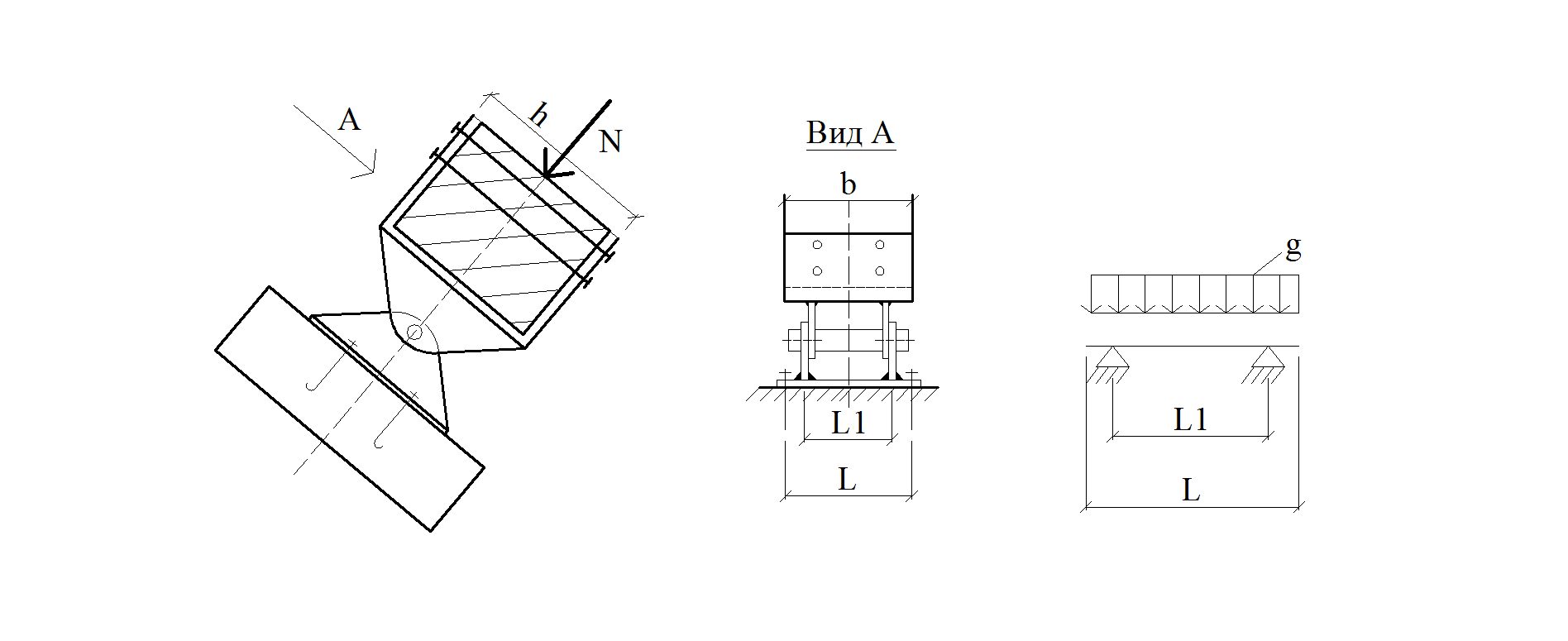
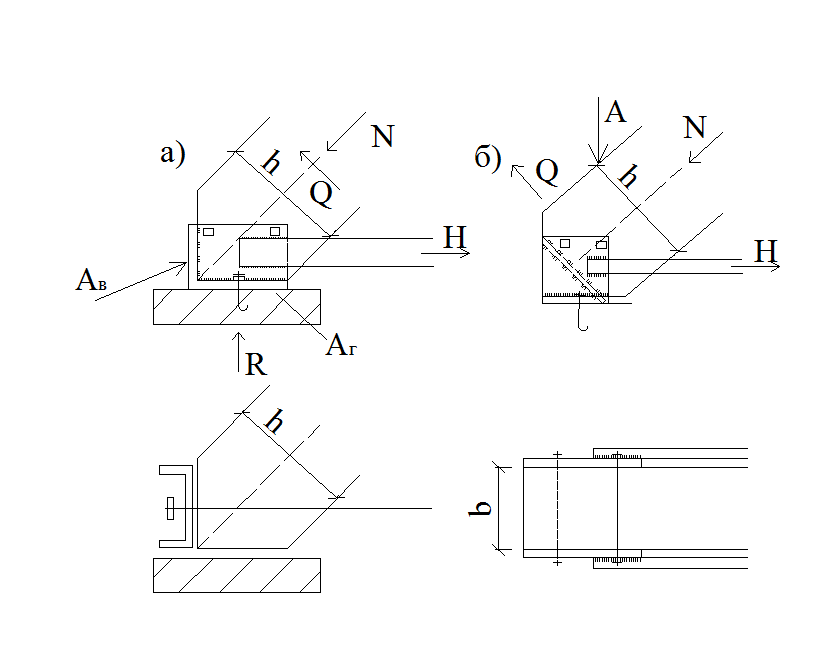
Рис. 1.12. Опорный узел арки с затяжкой При расчете по варианту «а» нижняя опорная поверхность рассчитывается на вертикальную составляющую силы N–R: Вертикальная поверхность упора рассчитывается на смятие диафрагмой от горизонтального усилия: Опорный лист этого башмака работает на изгиб, как стальная пластина, опертая по трем сторонам. В опорном узле с наклонной ребристой диафрагмой торец полуарки рассчитывается на смятие силой N. Число болтов определяется по величине Q, а диафрагма рассчитывается на изгиб как балка с пролетом равным расстоянию между пластинами b.
Сварные швы затяжки рассчитываются на силу H. Анкерные болты арок с затяжками рассчитываются косвенно на Q или устанавливаются конструктивно.
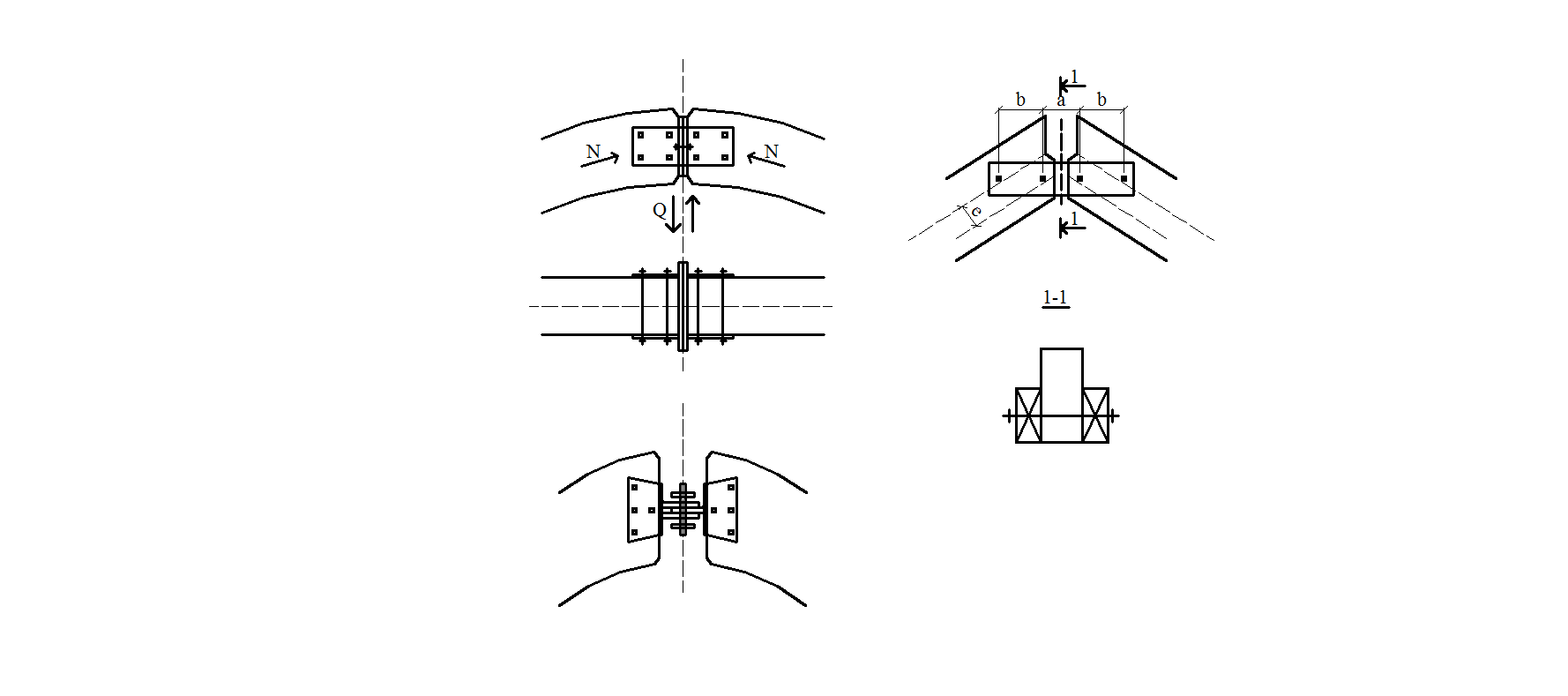
3) Расчет коньковых узлов Расчет коньковых узлов сегментной арки со стальными узловыми элементами производится по прочности лобовых упоров торцов полуарок. Число двусрезных симметричных болтов, соединяющих концы полуарок с фасонками, определяется по величине поперечной силы Q, действующей под углом
Рис. 1.13. Коньковый узел арок: а) большого пролета, б) небольшого, в) с деревянными накладками
Рис. 1.14. Расчетная схема узла с накладками
Круговая арка 2.1. Основные положения по проектированию Клееные деревянные арки рекомендуется проектировать, как правило, трехшарнирными, статически определимыми. Пролеты арок составляют 18...60 м и более (за рубежом имеются примеры применения клееных арок пролетом до 250 м). Шаг арок определяется технико-экономическим расчетом (3; 4,5; 6 м). Наибольшее распространение в строительстве получили арки кругового и стрельчатого очертания. Статический расчет арок ведется по общим правилам строительной механики на персональных компьютерах с использованием стандартных программ (например, «Лира»).
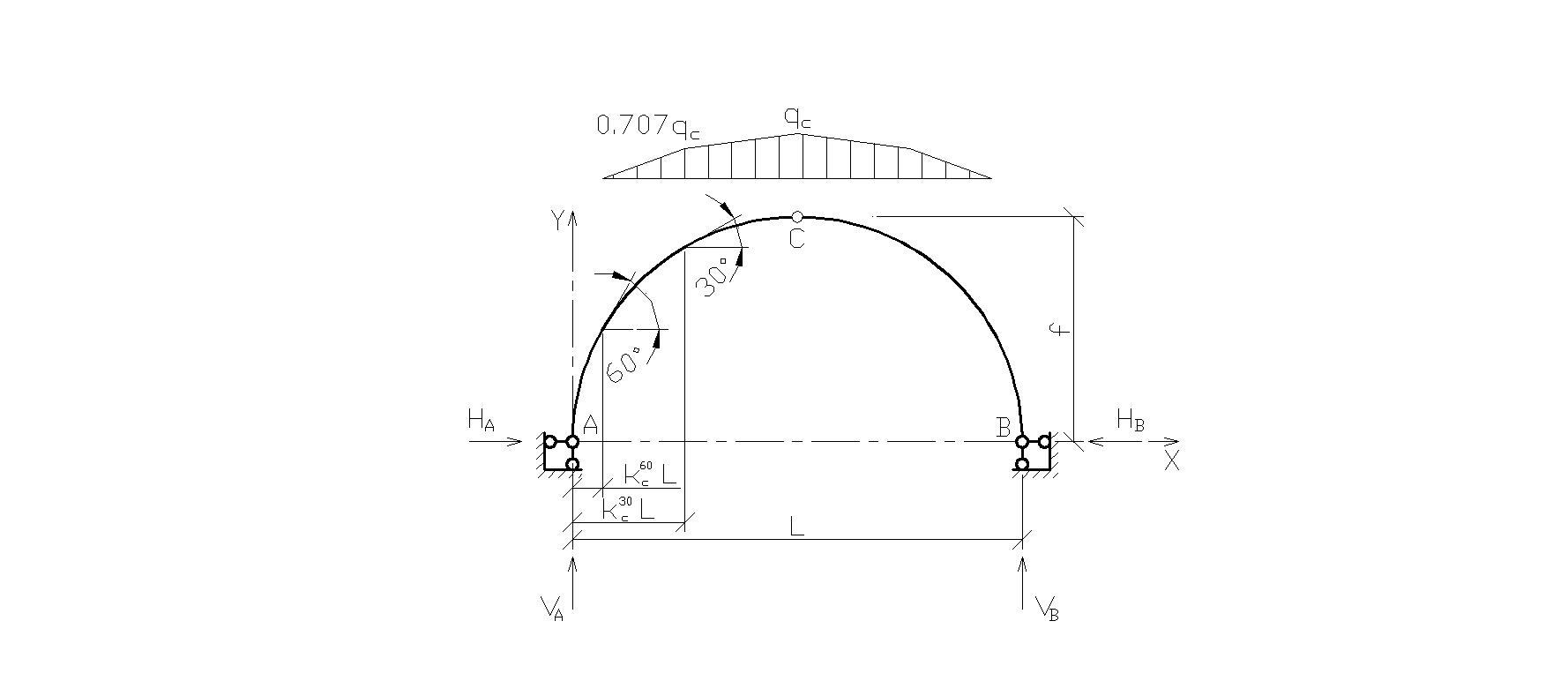
Рис. 2.1. Расчетная схема
1. По СП 20.13330.2011 «Нагрузки и воздействия» снеговая нагрузка к зданиям со сводчатыми и близкими к ним по очертанию покрытиями (приложение Г.2.1.) прикладывается как распределенная по параболе, которую, при ведении статического расчета «вручную», можно разложить на треугольную и трапецеидальную следующим образом: 1)
Рис. 2.2. Снеговая нагрузка по параболе в виде ломаной хорды
2)
В случае пологой арки, когда не образуется на покрытии угол в 60˚, расчет ведется по формулам:
Рис. 2.3. Снеговая нагрузка по параболе в виде трапеции
1)
2)
2. Также по СП 20.13330.2011 «Нагрузки и воздействия» снеговая нагрузка к зданиям со сводчатыми и близкими к ним по очертанию покрытиями (приложение Г.2.1) прикладывается как неравномерно распределенная по треугольнику:
Рис. 2.4. Снеговая нагрузка по «треугольнику»
Если угол 60º лежит в пределах арки, то усилия от снеговой нагрузки, распределенной по треугольнику на всём пролете, определяются по формулам: 1)
2)
3)
В случае, когда снег лежит наоборот расчет примет вид:
Рис. 2.5. Снеговая нагрузка зеркально по «треугольнику» 1)
2)
3)
В случае пологой арки, когда не образуется на покрытии угол в 60˚, расчет ведется по формулам: 1)
Рис. 2.6. Снеговая нагрузка по «неполному треугольнику»
2)
В случае, когда снег лежит наоборот расчет примет вид: 1)
Рис. 2.7. Снеговая нагрузка зеркальному по «неполному треугольнику»
2)
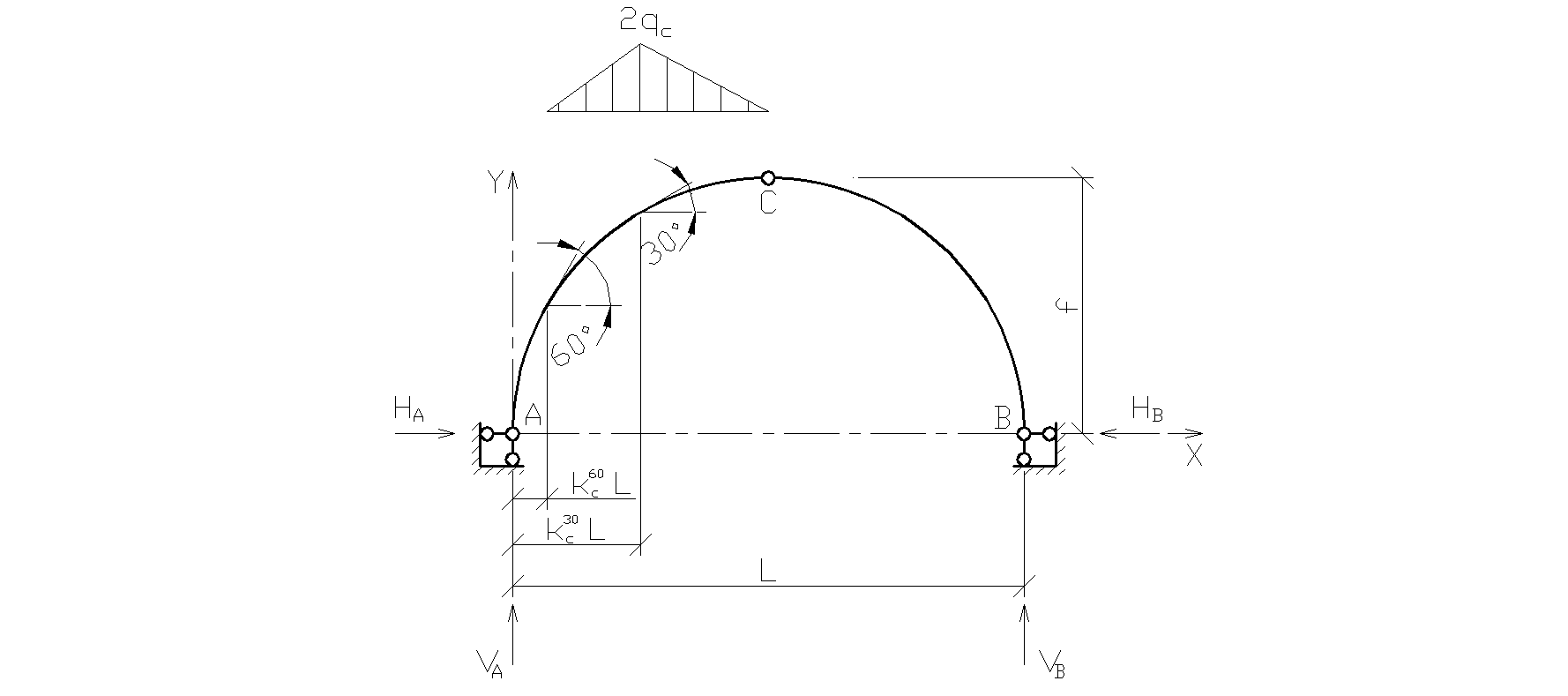
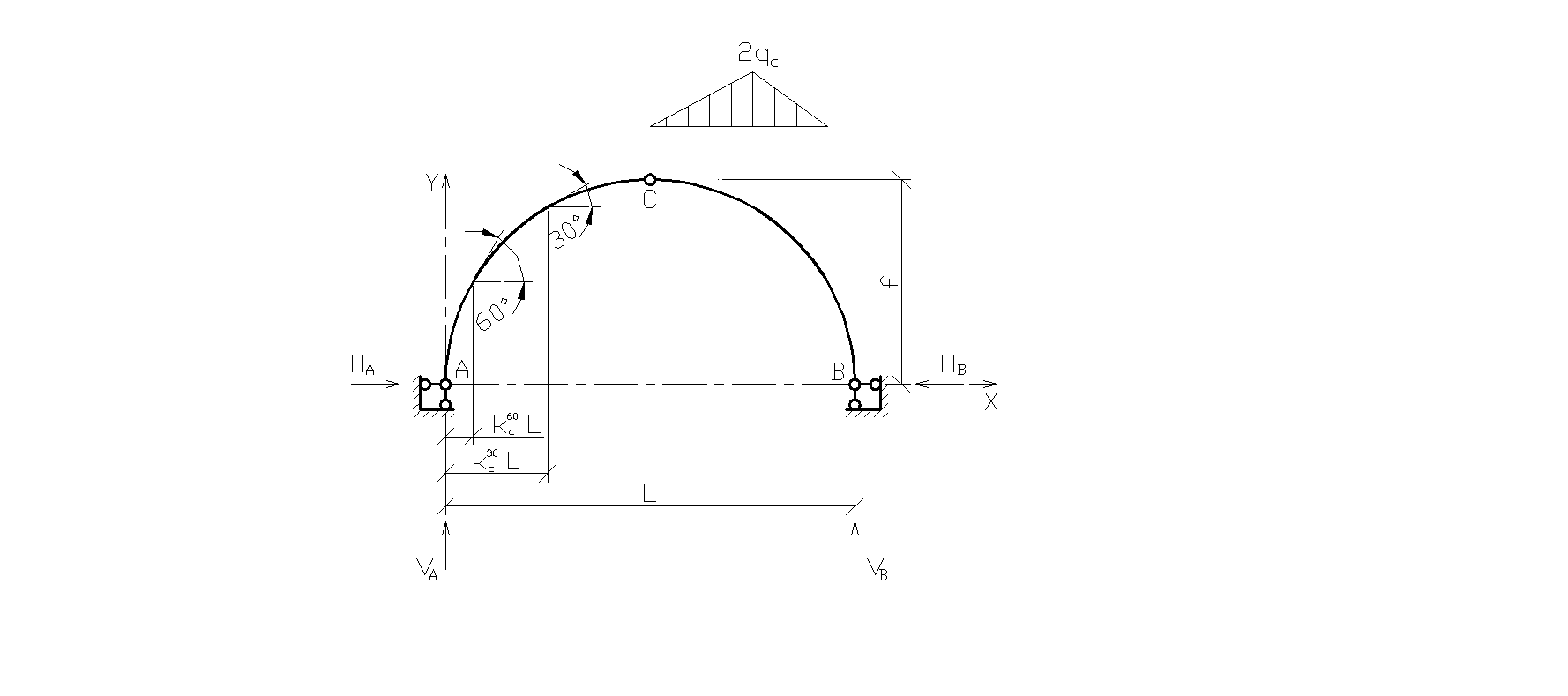
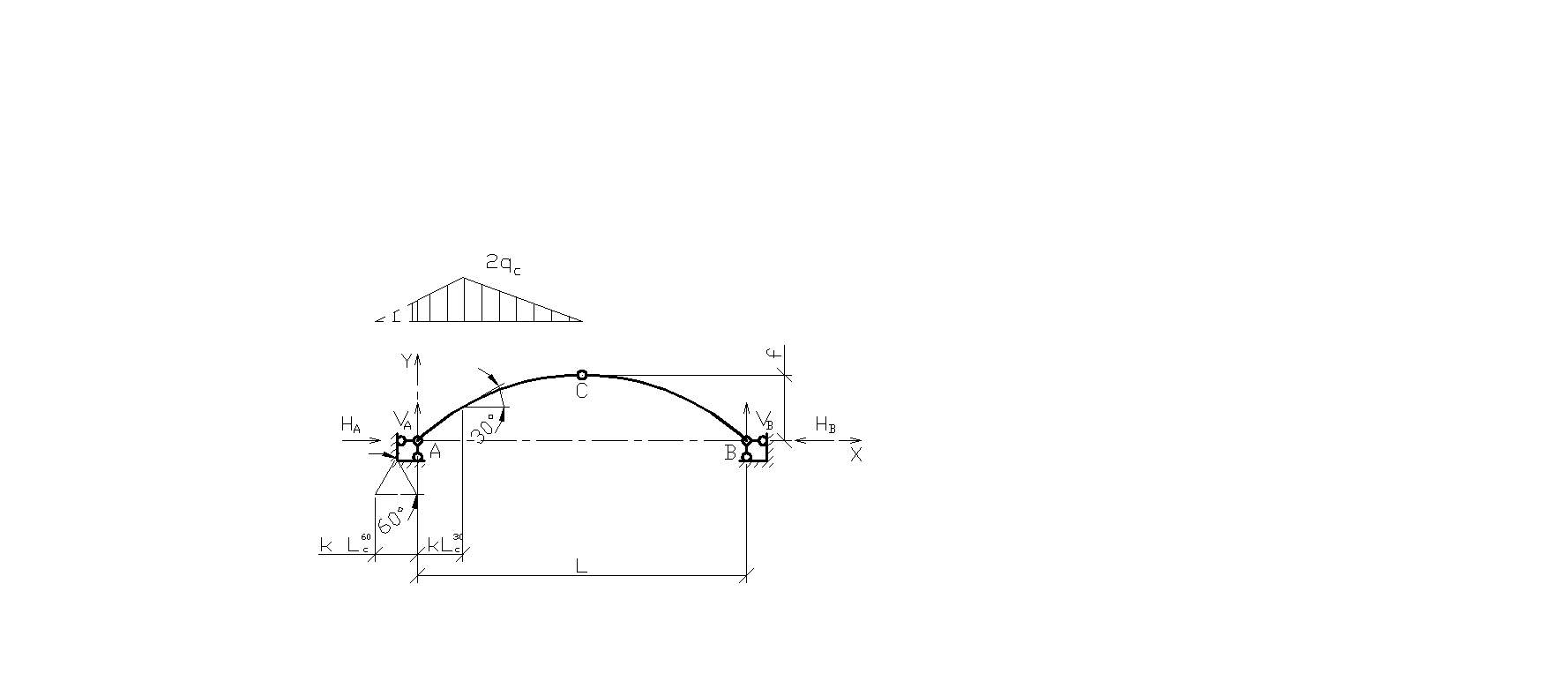
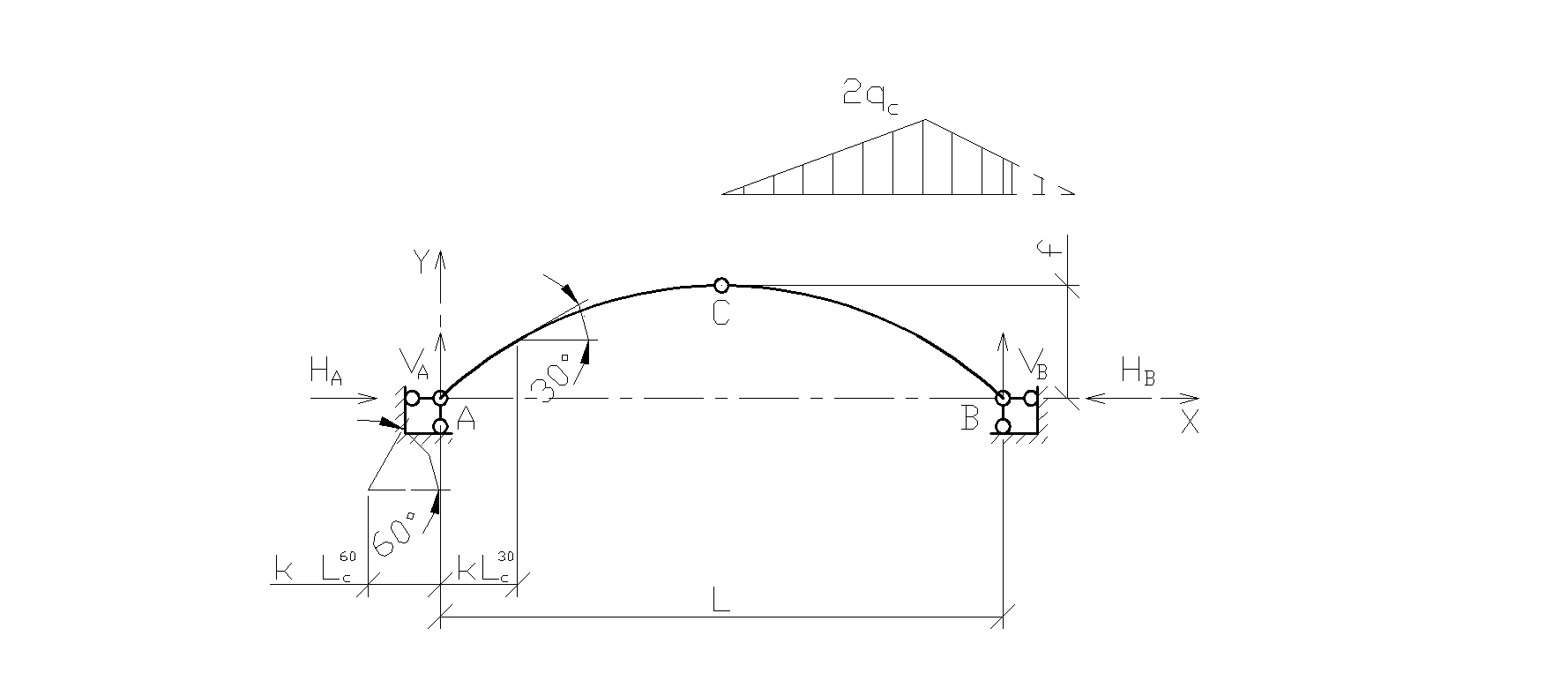
2. Третий вариант снеговой нагрузки рассмотрим как распределенную по треугольнику на полупролете слева: 1)
Рис. 2.8. Снеговая нагрузка на левой полуарке 2)
3)
В случае, когда снег лежит наоборот на полупролете справа расчет примет вид:
Рис. 2.9. Снеговая нагрузка на правой полуарке
В случае пологой арки, когда не образуется на покрытии угол в 60˚, расчет ведется по формулам:
Рис. 2.10. Снеговая нагрузка на левой полуарке по «неполному треугольнику»
1)
2)
В случае, когда снег лежит наоборот расчет примет вид:
1)
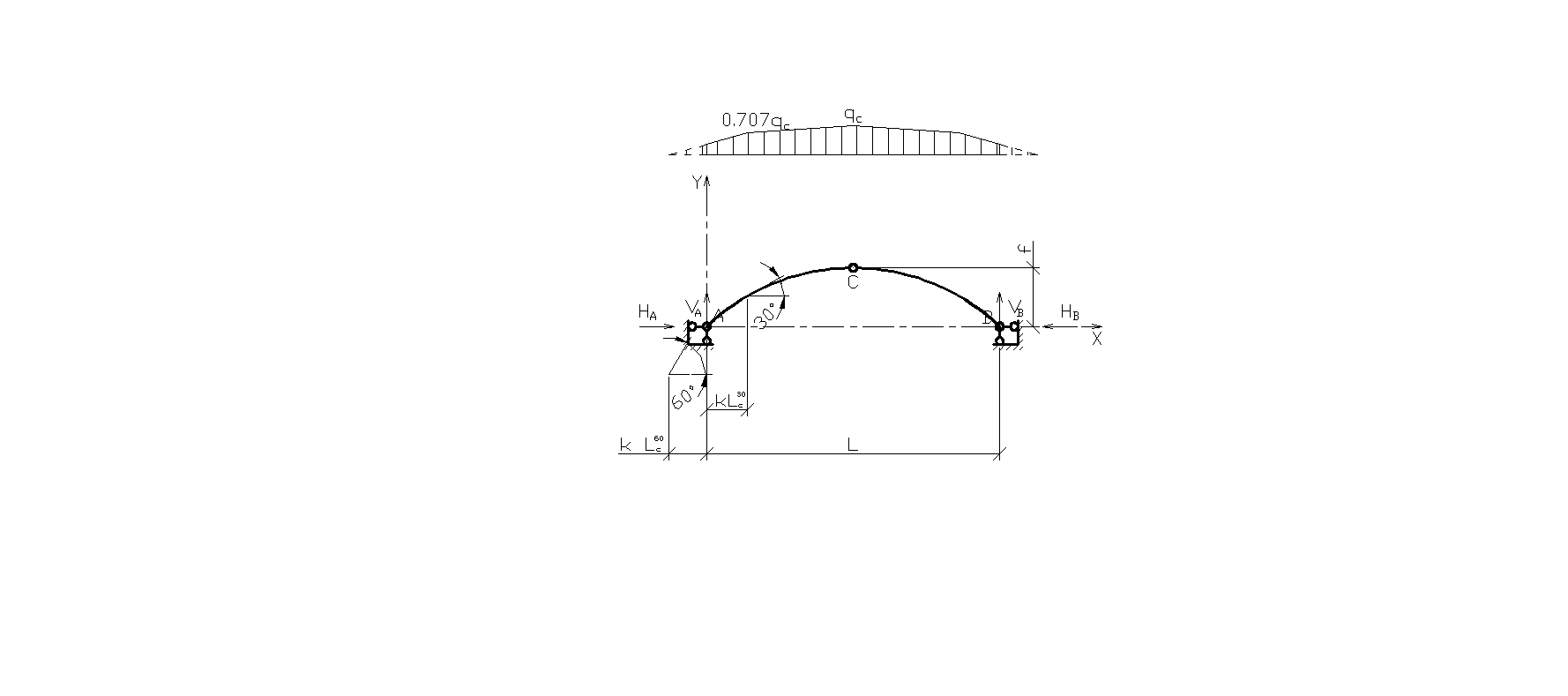
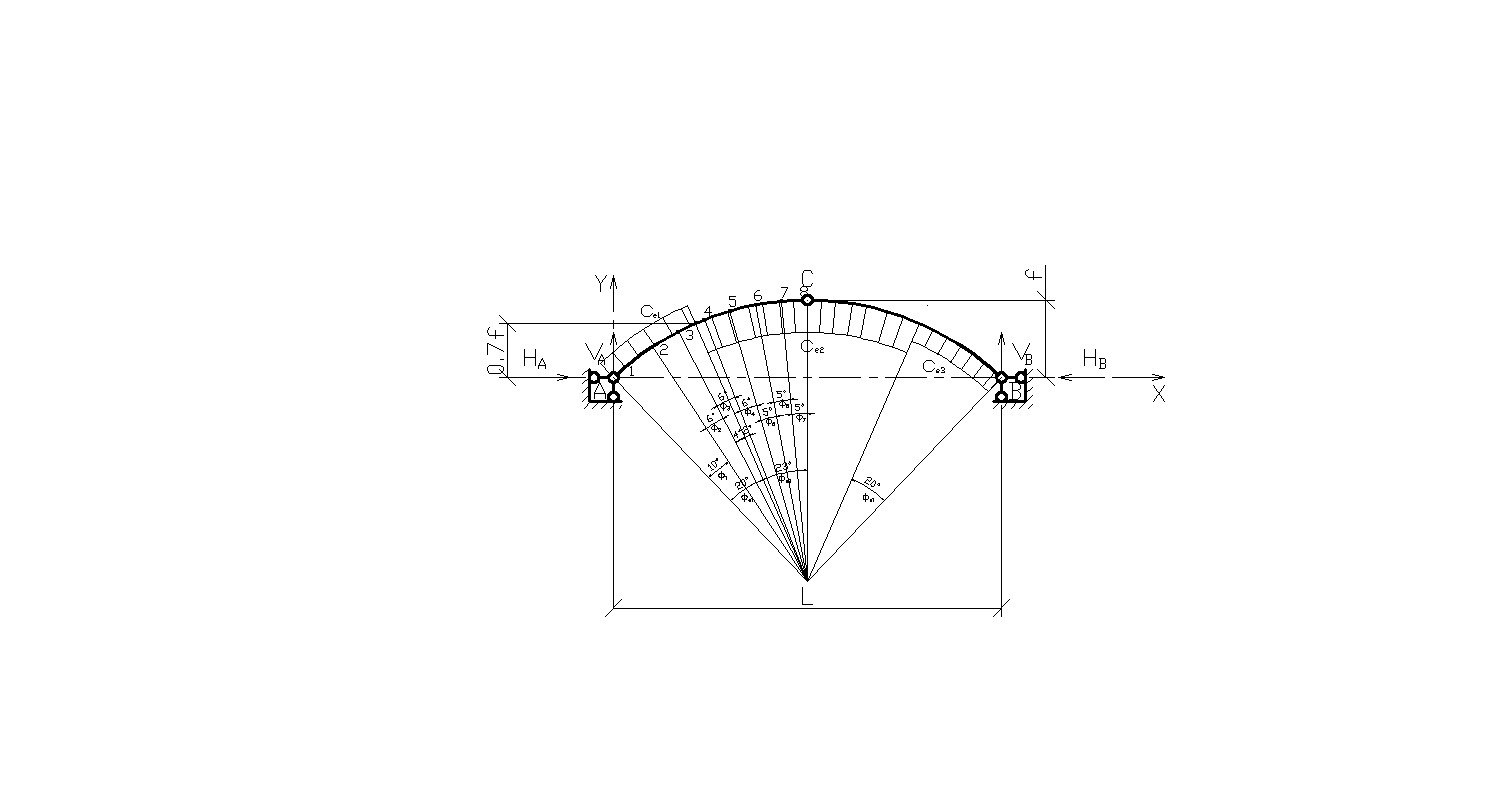
3. По СП 20.13330.2011 «Нагрузки и воздействия» ветровая нагрузка к зданиям со сводчатыми и близкими к ним по очертанию покрытиями (приложение Д.1.3) прикладывается следующим образом (углы должны быть в радианах): 1) т.1:
2) т.2:
Рис. 2.12. Ветровая нагрузка на арку 3) т.3:
4) т.4:
5) т.5:
6) т.6:
7) т.7:
8) т.8:
Аналогичные формулы для правой половины арки, только вместо реакций
Рис. 2.13. Ветровая нагрузка на арку Расчетным сечением арок является сечение с максимальным изгибающим моментом от наиболее невыгодного сочетания нагрузок. При том же сочетании нагрузок определяются значения продольной силы в расчетном сечении и величины продольных и поперечных сил в коньковом и опорном узлах арки. Конструктивный расчет арок заключается в подборе поперечного сечения по формулам для сжато-изгибаемых элементов в соответствии с требованиями СП 64.13330.2011, основные формулы для расчета сжато-изгибаемых элементов приведены также в СП. При расчете арок на прочность и устойчивость в плоскости кривизны расчетная длина l 0 принимается: - для трехшарнирных арок при симметричной и несимметричной нагрузках и двухшарнирных арок при несимметричной нагрузке l 0= 0,585; - для двухшарнирных арок при симметричной нагрузке l 0= 0,355; - для стрельчатых и треугольных арок l 0 = 0.5S, где S - длина дуги всей арки. При расчете арок на прочность по деформированной схеме и на устойчивость плоской формы деформирования, в формулу определения коэффициента ξ учитывающего дополнительный момент от продольной силы при деформации оси элемента, подставляется значение продольной силы в коньковом узле Nk:
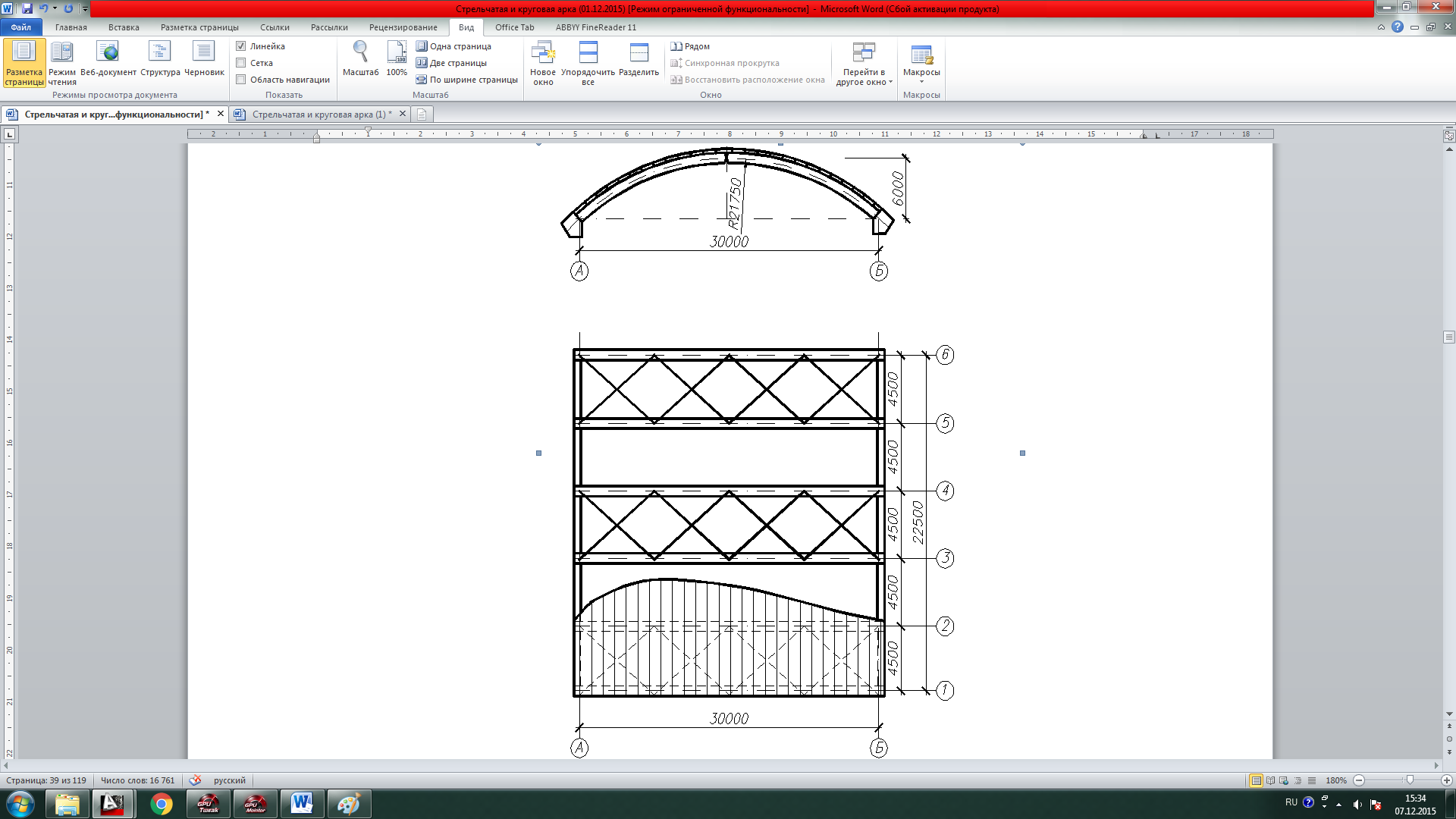
После подбора сечения арки конструируются и рассчитываются коньковый и опорный узлы. Пример расчета круговой арки Расчет можно выполнить полностью вручную, или же частично с применением ПК «ЛИРА». Мы приведем пример выполнение расчета ручным способом и автоматизированным в ПК «ЛИРА». Для выполнения расчета ПК нам необходимо для начала произвести сбор нагрузок, затем выполнить все пункты в ПК, и после этого продолжить ручной расчет. Задание: спроектировать и рассчитать трехшарнирную круговую гнутоклееную арку покрытия склада с классом эксплуатации А1. Арка постоянного прямоугольного сечения, пролет l = 30 м, стрела подъема f = 6 м > l/6 при шаге 4,5 м, опоры железобетонные (рис. 2.14). Район строительства III по снеговой нагрузке.
Рис. 2.14. Поперечный разрез и план арочного покрытия
Класс ответственности здания II, следовательно γп =1 (Приложение 1.18). Ограждающая часть покрытия состоит из утепленных плит размером 1х4.5 м, укладываемых непосредственно на арки. По плитам устраивается кровля из оцинкованной стали. Устойчивость арок из плоскости обеспечивается продольными деревянными ребрами плит и стальными диагональными тяжами, которые расположены в торцах здания и через 24 м вдоль здания, образуя поперечные связевые фермы. Продольные ребра плит прикреплены к верхним граням арок, а в коньке и пятах полуарок поставлены продольные элементы распорки с упором в боковые грани арок.
Решение Геометрические размеры арки При расчетном пролете l = 30 м и стреле подъема ее f = 6 м радиус арки находим по формуле: r = (l2+4 f2)/(8f) = (302 + 4∙62)/(8∙6) = 21,75 м Центральный угол дуги полуарки α определяем из выражения: cosα = (r - f)/r = (21,75 - 6)/ 21,75 = 0,724, откуда α = 43°36’. Центральный угол дуги арки 2 α = 87°12’, длина друга арки: S = (πr∙2α)/180° = (3,14∙21,75∙87,2°)/180° = 33,08 м. Координаты точек оси арки у для вычисления моментов М находятся по формуле:
где Д = r – f = 21,75 -6 = 15,75 м и приведены в таблице 2.1.
Таблица 2.1
Нагрузки Постоянные расчетные нагрузки на 1 м2 горизонтальной проекции покрытия определяются с введением коэффициента перегрузки n в соответствии с СП 20.13330.2011, пп. Г.2.1. Нормативные нагрузки умножаются на коэффициент k = S/l =33,08/30 = 1,1, учитывающий разницу между длиной дуги арки и ее проекцией. Вес снегового покрова для III района Sg = 240 кг/м2 горизонтальной проекции; нормативная равномерно распределенная снеговая нагрузка по формуле 10.1 СП 20.13330.2011: S0 = 0,7се сtµ Sg = 0,7*0,85*1*µ*240 кг/м2 = 142,8 µ кг/ м2 Тогда расчетная снеговая нагрузка на 1 м2 горизонтальной проекции покрытия: Sр = γf Sо=1,4* 142,8µ=199,92 µ кг/м2 Собственный вес арки в зависимости от нормативного веса кровли и снега определим по формуле: gсвн = (gпн + Рснн)/[1000/(Ксв l) - 1]= (54,2+142,8)/[1000/(4∙30)-1]= 26,86 кг/м2 Сбор постоянных нагрузок арочного покрытия приведен в таблице 2.2. Полная нормативная нагрузка от собственного веса gн =81.06 кг/м2 горизонтальной проекции. Таблица 2.2
*нагрузка от плиты покрытия принята из занятия 3[13].
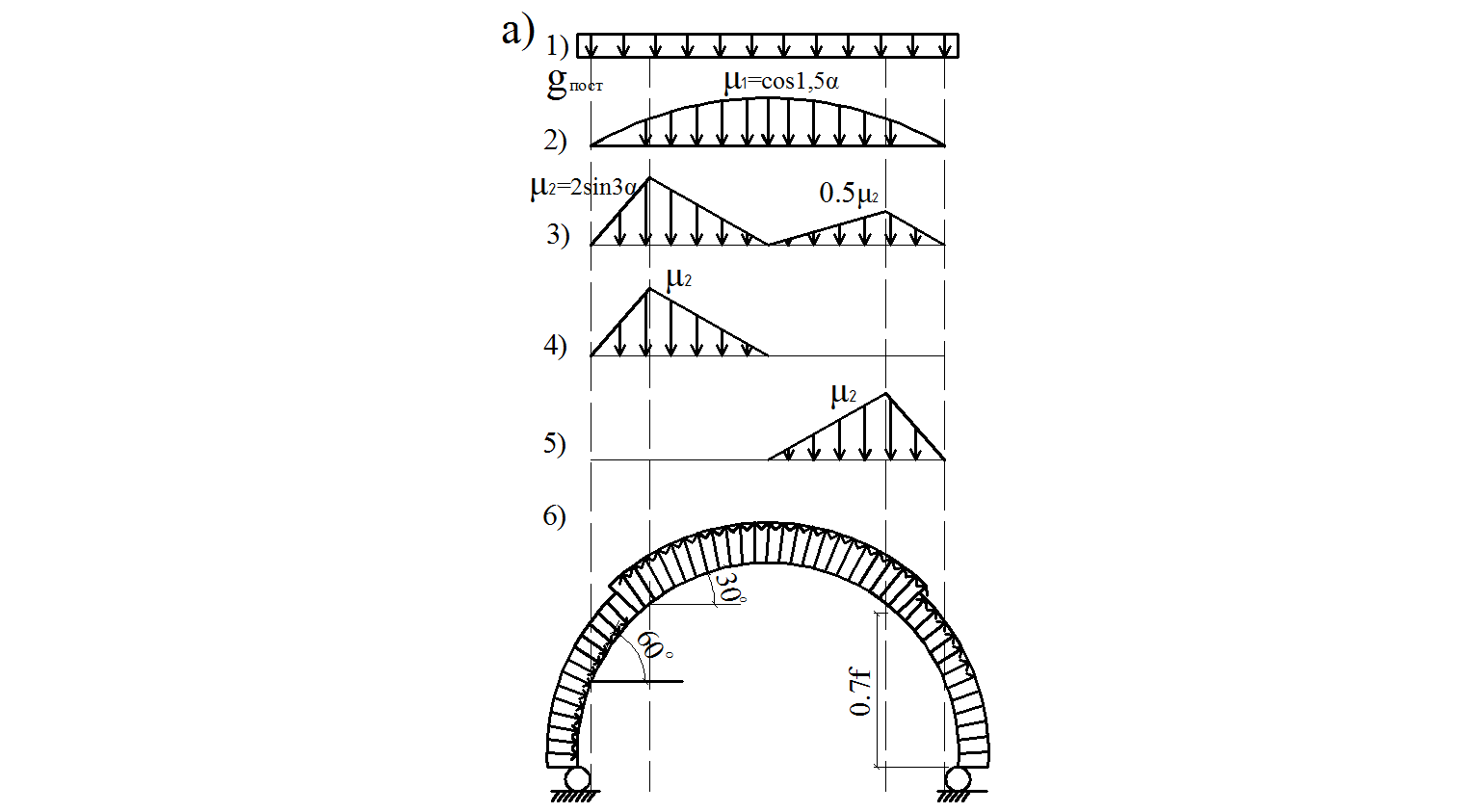
При снеговой нагрузке, распределенной по треугольнику, коэффициент μ1 =2 sin 3 ∙ α= 2 sin 3 ∙ 30’ = 2 и Р1 = 199,92 µ1 =199,92 ∙2 = 399,84кг/м2 При снеговой нагрузке, распределенной по параболе, коэффициент μ 2 = cos1,5 ∙ α При х=0м: Р2 = 199,92 cos1,5 ∙ α =199,92 cos1,5 ∙ 43.6 = 83,22кг/м2 При х=3м: Р2 = 199,92 cos1,5 ∙ α =199,92 cos1,5 ∙ 33.48 = 127,92кг/м2 При х=5м: Р2 = 199,92 cos1,5 ∙ α =199,92 cos1,5 ∙ 27.37 = 150,76кг/м2 При х=7м: Р2 = 199,92 cos1,5 ∙ α =199,92 cos1,5 ∙ 21.58 = 168,85кг/м2 При х=9м: Р2 = 199,92 cos1,5 ∙ α =199,92 cos1,5 ∙ 16.01 = 182,61кг/м2 При х=11м: Р2 = 199,92 cos1,5 ∙ α =199,92 cos1,5 ∙ 10.59 = 192,29кг/м2 При х=13м: Р2 = 199,92 cos1,5 ∙ α =199,92 cos1,5 ∙ 5.27 = 198,02кг/м2 При х=15м: Р2 = 199,92 cos1,5 ∙ α =199,92 cos1,5 ∙ 0 = 199,92кг/м2
Расчетные нагрузки, приходя
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 1881; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.105.101 (0.018 с.) |

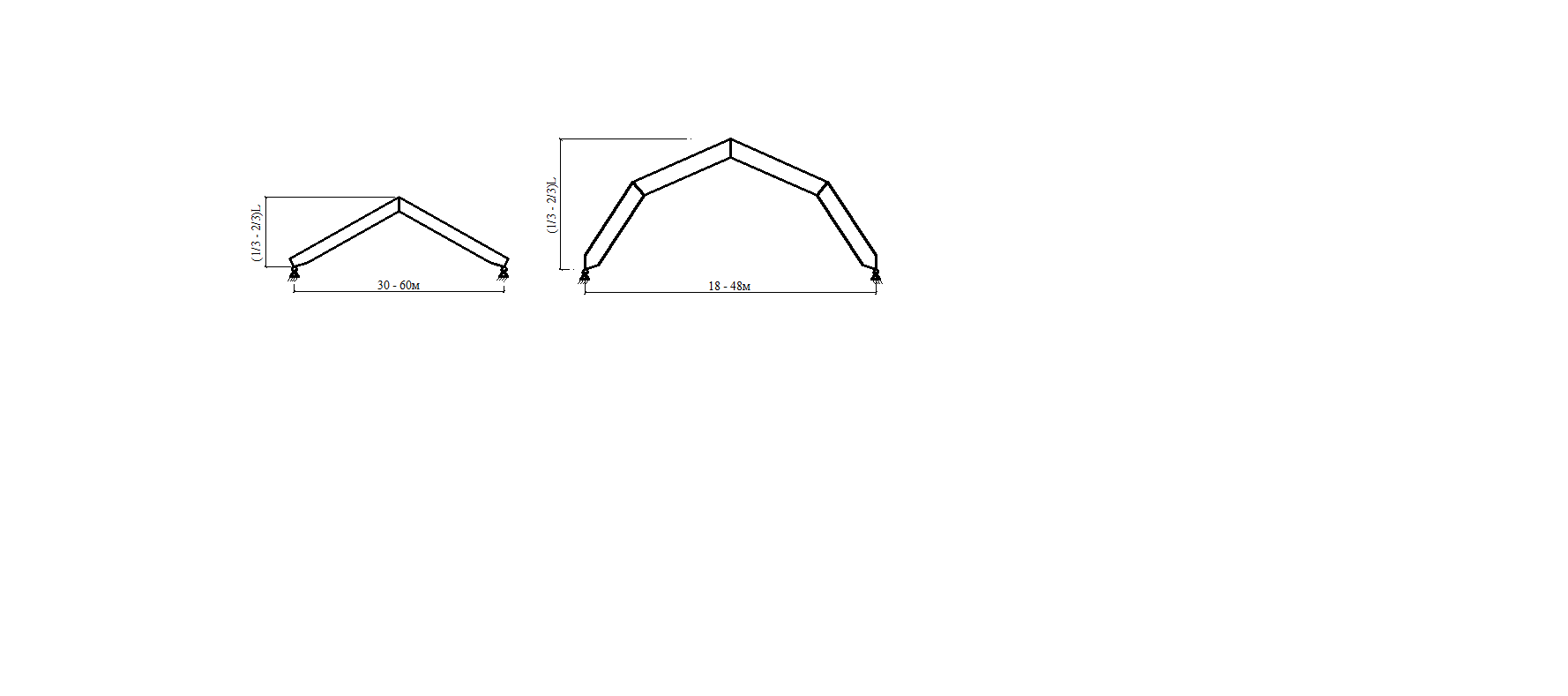

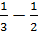 )L без затяжек и (
)L без затяжек и (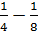 )L с затяжками и пролетом до 24м. пояса таких арок имеют сечение шириной не более 17см, что позволяет склеивать их из целых досок в один ряд. Затяжки арок выполняют из арматурной и профильной стали.
)L с затяжками и пролетом до 24м. пояса таких арок имеют сечение шириной не более 17см, что позволяет склеивать их из целых досок в один ряд. Затяжки арок выполняют из арматурной и профильной стали.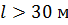 сплачивание по ширине.
сплачивание по ширине.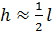 при
при 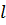 до 50 м. Сечение при больших пролетах собирается из 2 и 3 досок по ширине.
до 50 м. Сечение при больших пролетах собирается из 2 и 3 досок по ширине.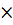 120 см. Разработаны типовые стрельчатые арки пролетом 18 и 24 м.
120 см. Разработаны типовые стрельчатые арки пролетом 18 и 24 м.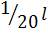 и гвоздевыми или болтовыми соединениями. Трудоемки. Требуют закрепления сжатых нижних поясов от потери устойчивости. Почти не применяются.
и гвоздевыми или болтовыми соединениями. Трудоемки. Требуют закрепления сжатых нижних поясов от потери устойчивости. Почти не применяются. и для стрельчатой арки R.
и для стрельчатой арки R.
 .
.

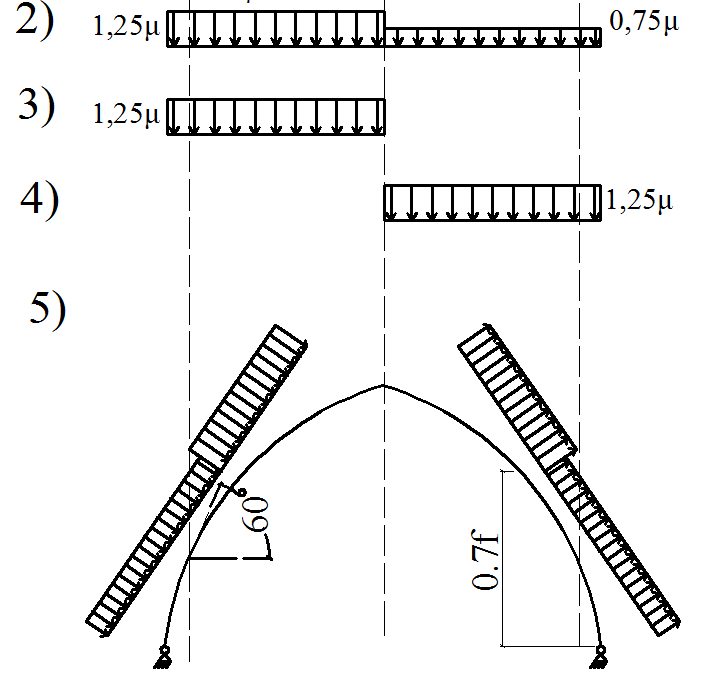
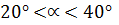 следует рассмотреть I и II варианты;
следует рассмотреть I и II варианты;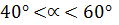
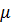 определяется интерполяцией с сохранением второго варианта:
определяется интерполяцией с сохранением второго варианта: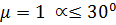
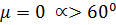
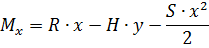
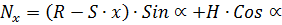
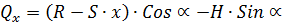
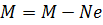 .
.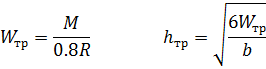
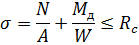
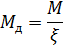
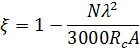
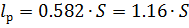 – треугольной и стрельчатой; S – длина полуарки.
– треугольной и стрельчатой; S – длина полуарки.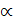 .
.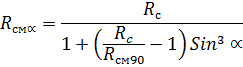
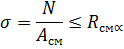
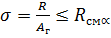 .
.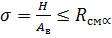
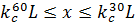
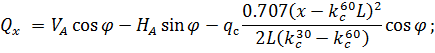
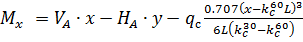 ;
;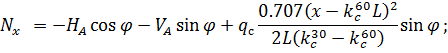
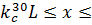
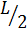
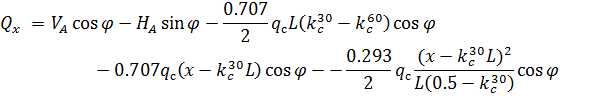
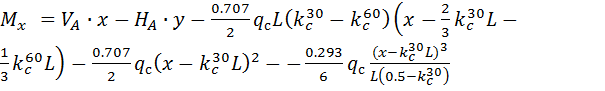
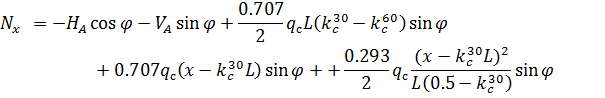
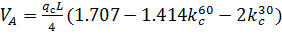 ;
;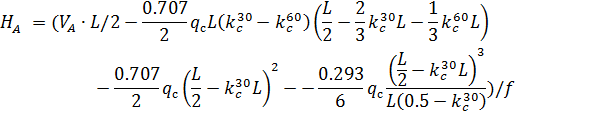
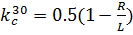 ;
; .
.
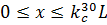
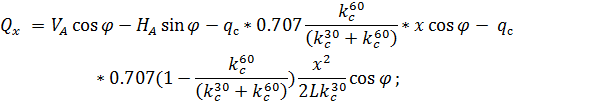
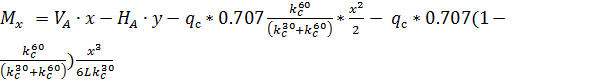 ;
;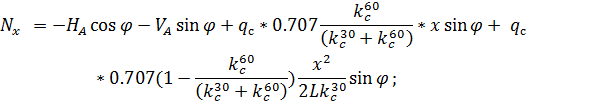
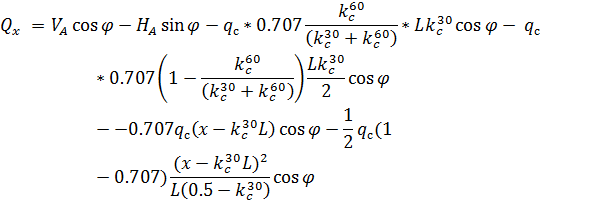
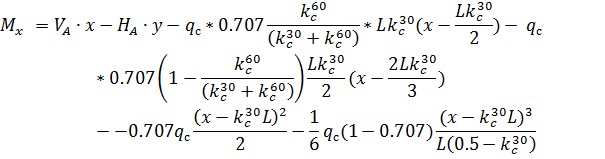
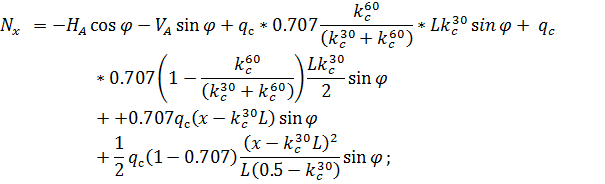
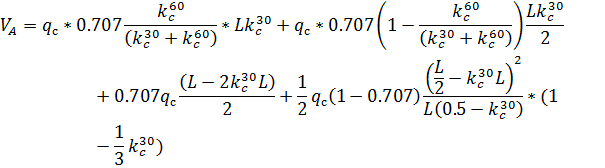
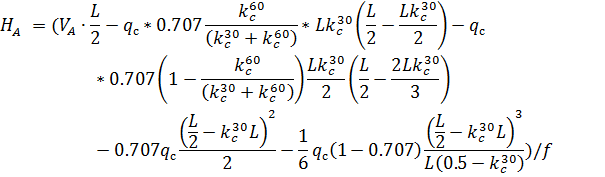
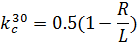
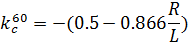
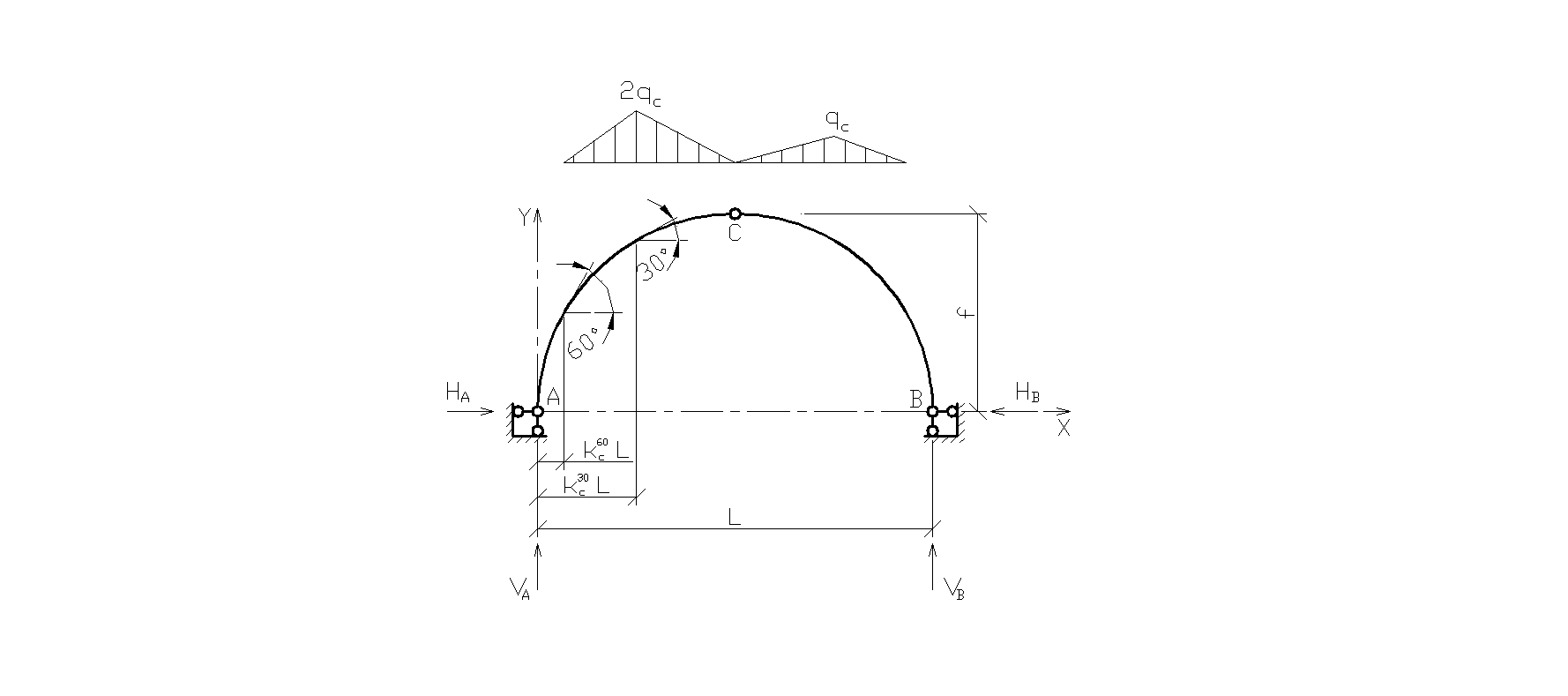
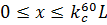
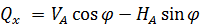
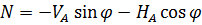
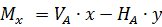
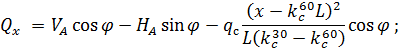
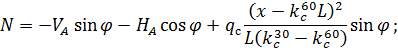
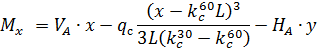
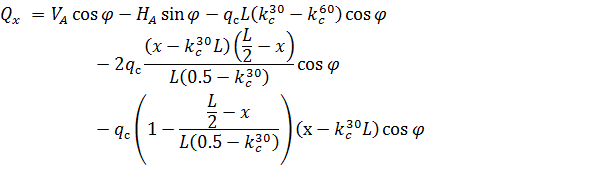
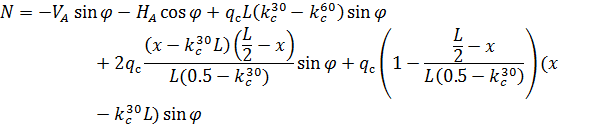
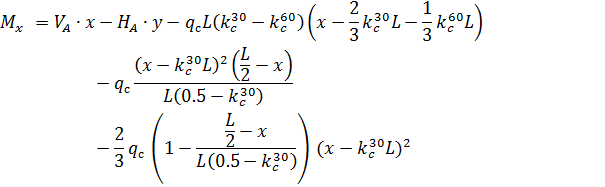
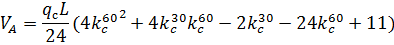
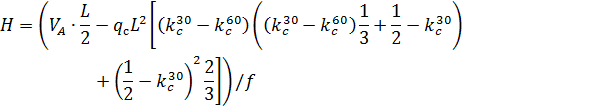
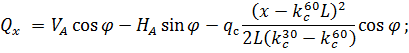
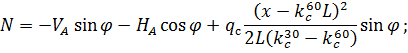
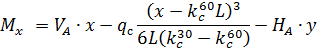
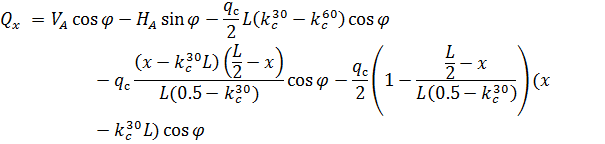
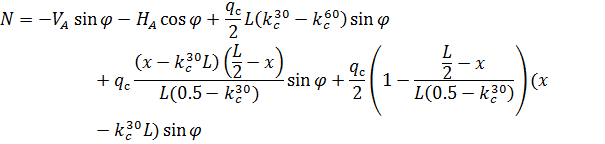
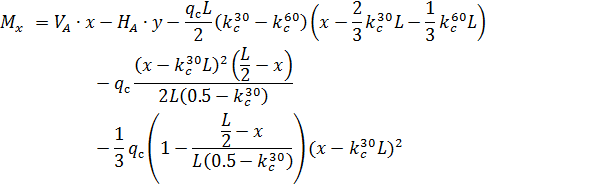
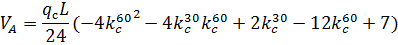
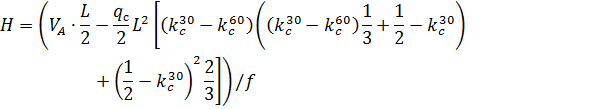
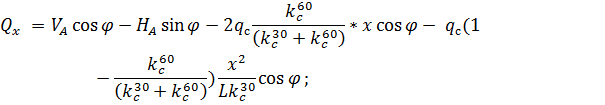
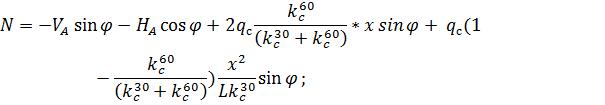
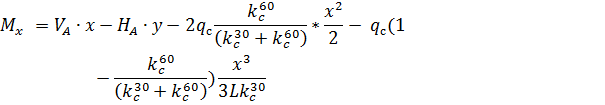
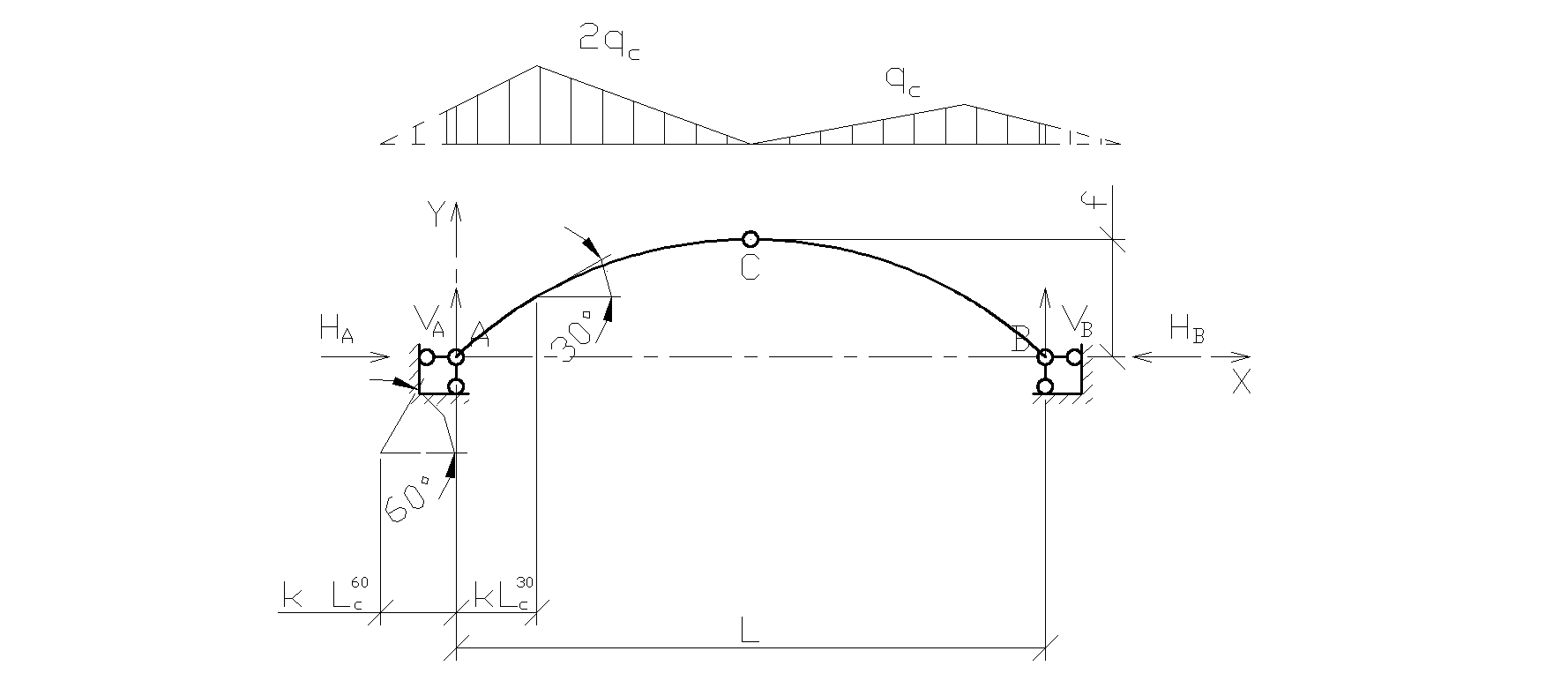
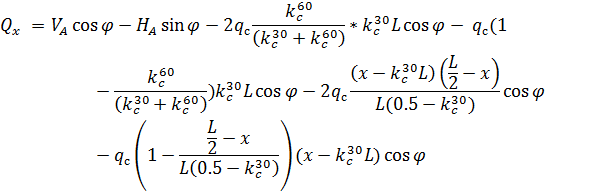
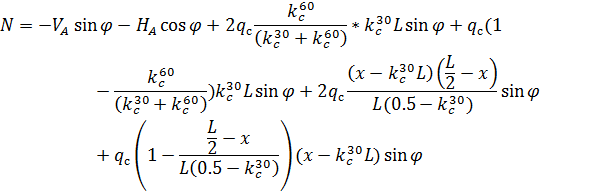
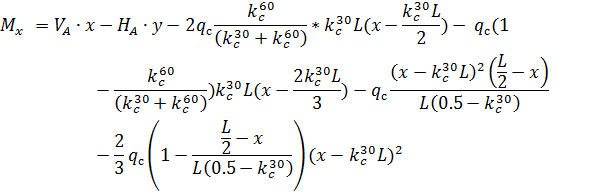
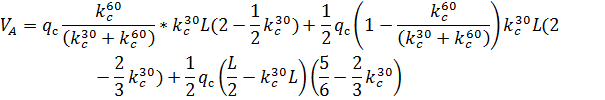
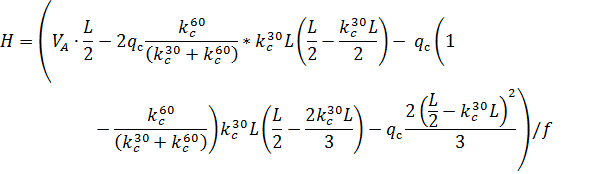
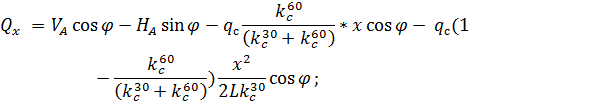
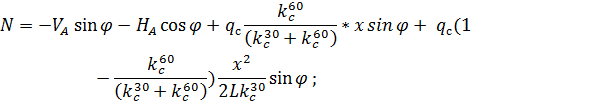
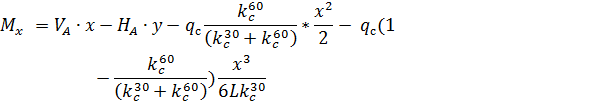
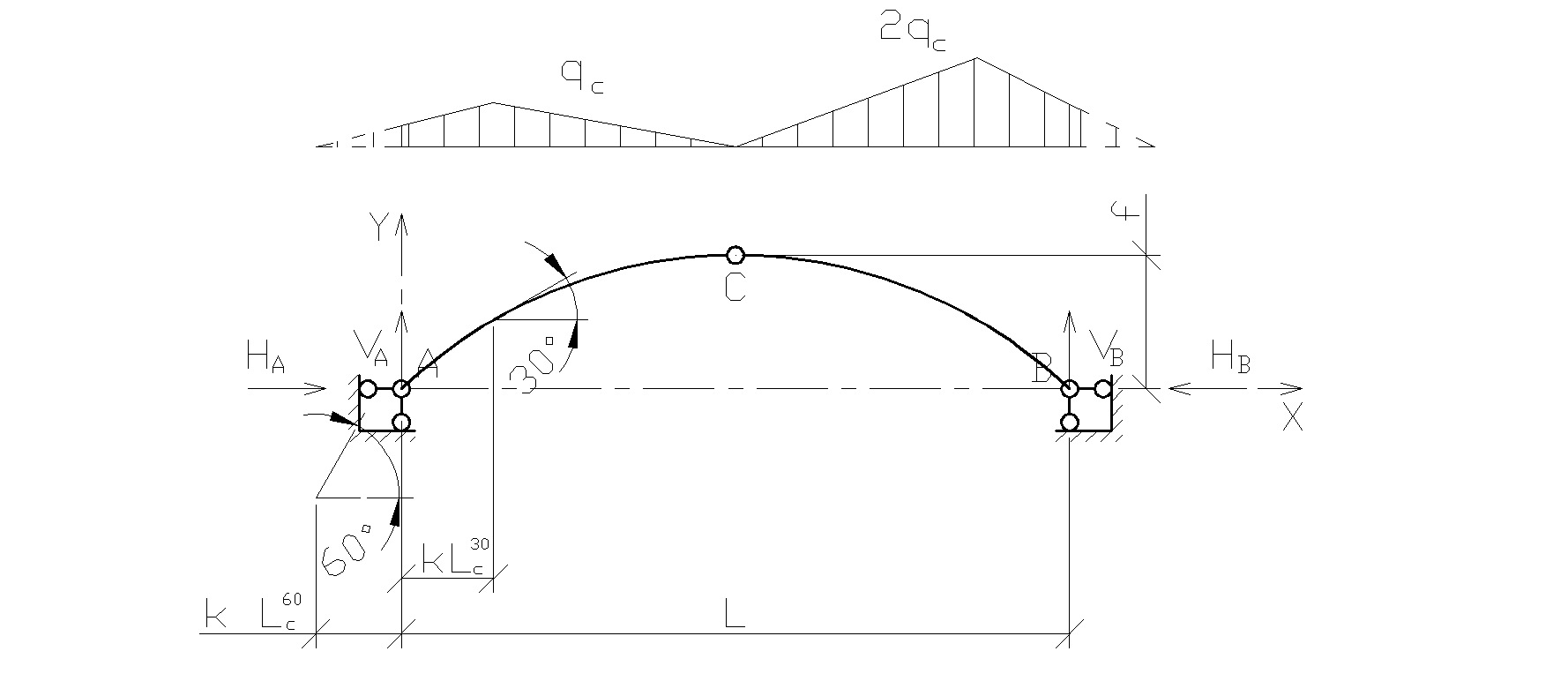
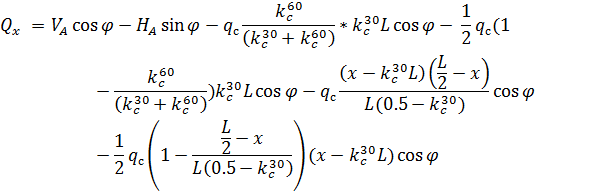
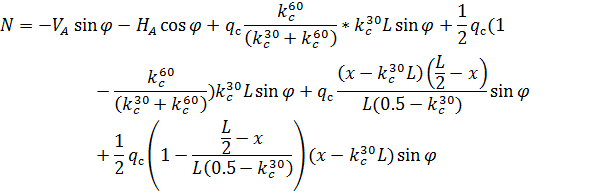
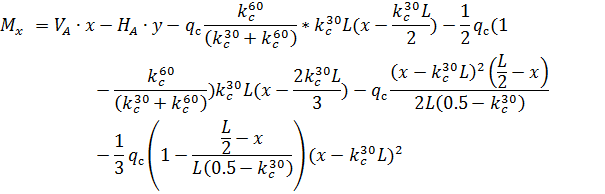
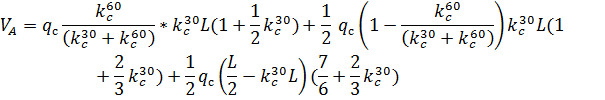
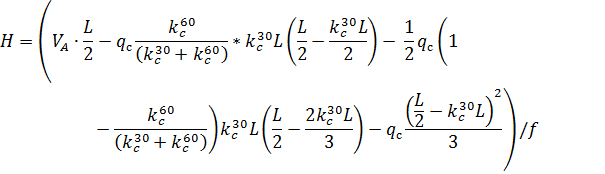
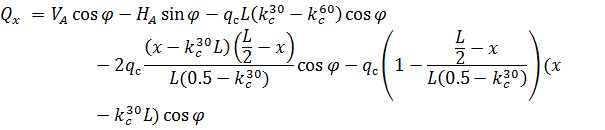
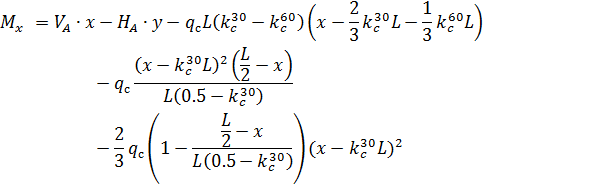

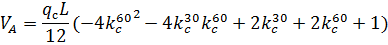
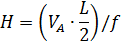
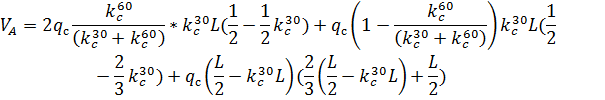
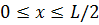
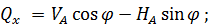
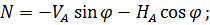
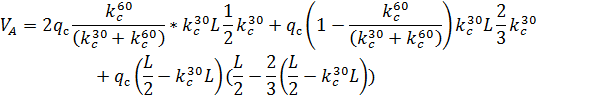
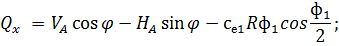
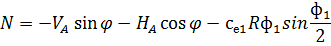
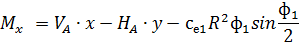
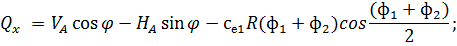
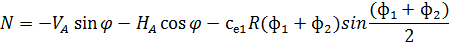
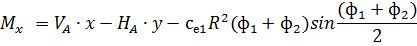
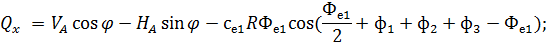
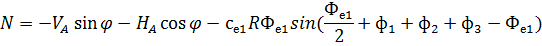
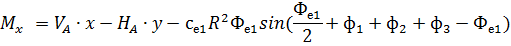
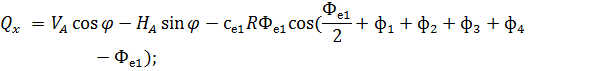
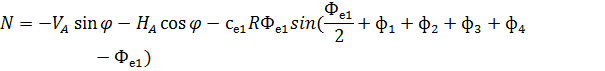
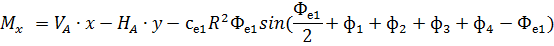
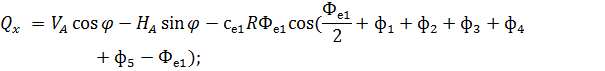
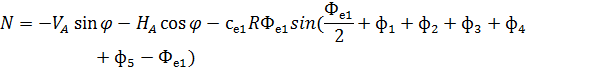
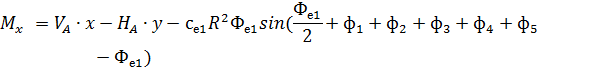
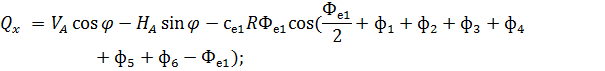
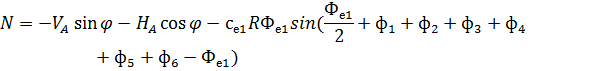
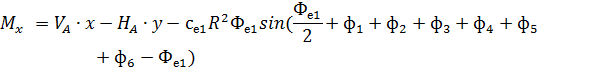
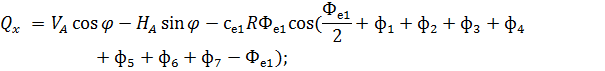
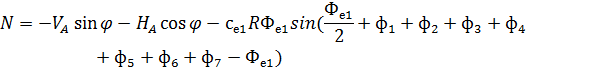
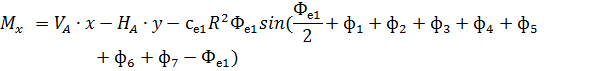
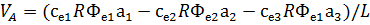
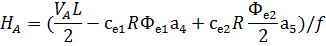
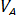 и
и 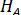 использовать реакции
использовать реакции 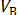 и
и 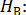
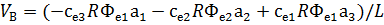
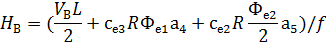
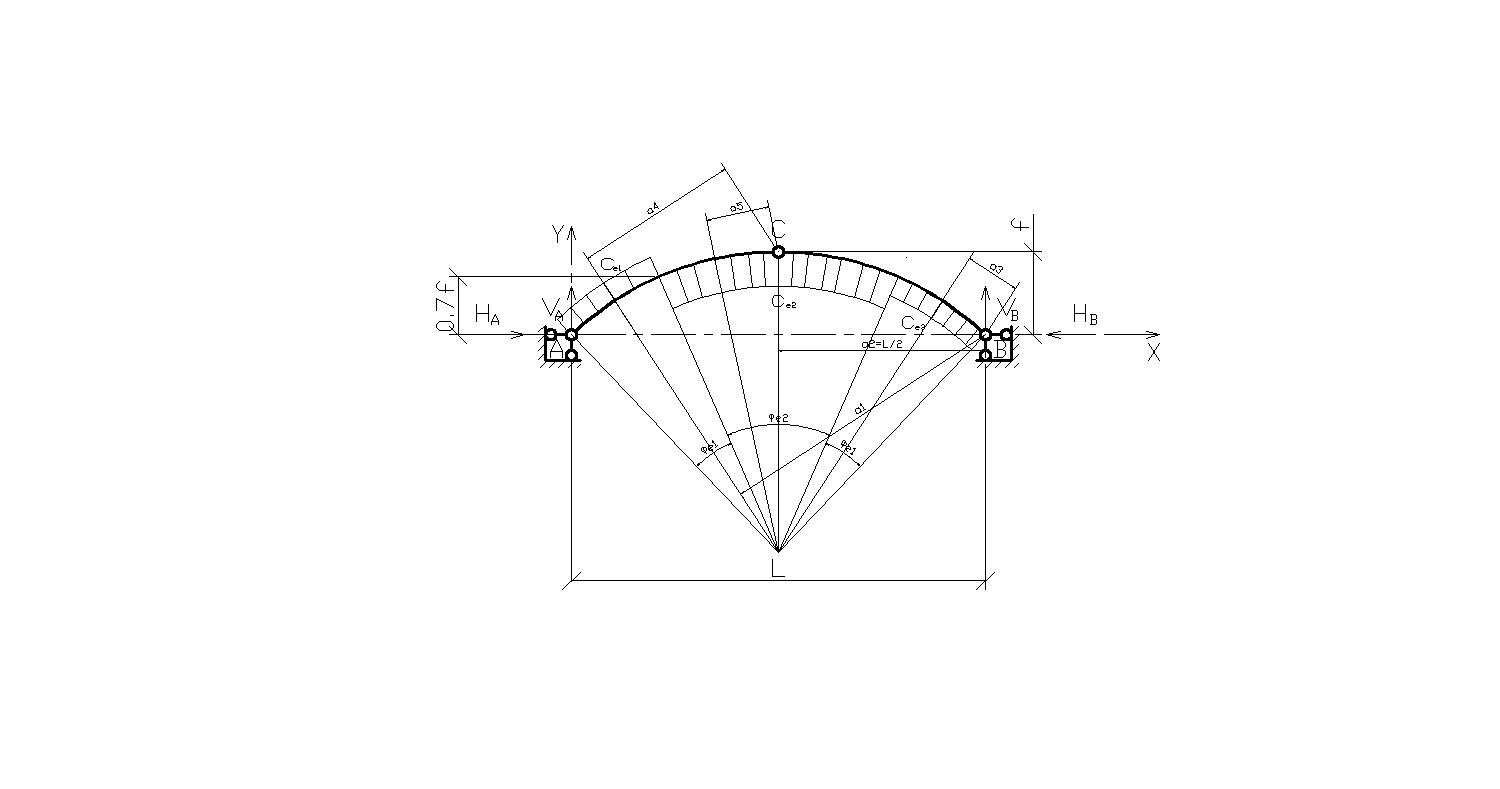
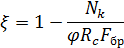
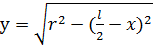 – Д,
– Д,


