
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Шаг 10. Просмотр и анализ результатовСодержание книги
Поиск на нашем сайте
· После расчета задачи, переход в режим результатов расчета осуществляется с помощью меню Режим Результаты расчета (кнопка · В режиме просмотра результатов расчета по умолчанию расчетная схема отображается с учетом перемещений узлов. Для отображения схемы без учета перемещений узлов выполните пункт меню Схема Исходная схема (кнопка ·
 , а затем , а затем  на панели инструментов). на панели инструментов).
· Для вывода эпюры QZ, выполните пункт меню Усилия Эпюры Эпюры поперечных сил (QZ) (кнопка · Для вывода эпюры N, выполните пункт меню Усилия Эпюры Эпюры продольных сил (N) (кнопка
Шаг 11. Формирование и просмотр таблиц результатов расчета · Для вывода на экран таблицы со значениями расчетных сочетаний усилий в элементах схемы, выполните пункт меню Окно Интерактивные таблицы. · После этого в диалоговом окне Редактор форм выделите строку Усилия (стержни). · Щелкните по кнопке Применить. · В диалоговом окне Создание таблицы элементов выберите Для всех загружений (рис. 2.37). · Нажмите Подтвердить.
Усилия в арке от нагрузок приведены в таблице 2.4. Расчетные усилия в арке: 1) постоянной (собственный вес арки); 2) снеговой, распределенной по треугольнику; 3) снеговой, распределенной по треугольнику на полупролете слева; 4) снеговой, распределенной по параболе; 5) ветровой; 6) динамические
Расчетные усилия в арке Таблица 2.4
Сочетания нагрузок по СП 20.13330.2011 «Нагрузки и воздействия». Усилия в арке от сочетания расчетных нагрузок: 1 – постоянной (1), снеговой (2) и ветровой (5) и динамика(6); 2- постоянной (1), снеговой (3) и ветровой (5) и динамика (6); 3 - постоянной (1), снеговой (4) и ветровой (5) и динамика (6).
Таблица 2.5
Усилия, полученные на ПК «Лира» больше усилий, полученных вручную (см. табл. 2.3) с учетом динамической составляющей по шестому загружению. Авторы проекта совместно с руководством принимают решение о необходимости учета динамики.
Подбор сечения круговой арки Расчетные усилия М23= - 11973,73 кг∙м; N23 = -12263,5 кг – расчетное сочетание усилий 2 из таблицы 2.3. М7 = 22003,82 кг∙м; N7 = -12009,4кг – расчетное сочетание усилий 2 из таблицы 2.3. Предварительное определение размеров поперечного сечения арок производим по СП 64.13330.2011, п. 6.17, формула (30): N/Fрасч + МД/Wрасч ≤ Rc. Приняв h/b = β, получим: h3 – βNh/ Rc - 6βM/(ξ Rc)= 0. (1) Это уравнение приводим к виду: h3 + 3рh + 2q = 0, где р = – βN/ 3Rc; q =- 3βM/(ξ Rc); β = 5÷6; ξ = 0,5÷0,8; Rc – расчетное сопротивление древесины сжатию с учетом коэффициентов условий работы по пп. 5.1 и 5.2 и коэффициентов надежности по назначению конструкций согласно стандарту. Поскольку q>>р, дискриминант приведенного уравнения Д = q2+ р3>0 и оно имеет одно действительное и два минимальных решения. Согласно по формуле Кардано, действительное решение h = U + V, где U = Подбор сечения арки Учитывая уникальный характер здания по степени ответственности, для изготовления арок принимаем пиломатериал из сосны 1-го сорта толщиной 4,2 см. Коэффициент надежности по назначению γn = 1. Оптимальная высота поперечного сечения арки находится в пределах (1/40 - 1/50) l = (1/40 - 1/50) 3000 = 75 - 60 см. Примем δсл = 4,2 см и rk/а = 2175/4,2 =517,86>500 коэффициенты условий работы будут mв = 1, mн = 1,2, mб = 0,915, mсл = 0,95, mгн = 1; соответственно расчетное сопротивление сжатию и изгибу: Rc = Rи =1*1,2 0,915∙0,95∙1,0∙14/1,0 =146 кг/см2 Для определения поперечных размеров сечения арки пользуемся уравнением (1). Принимаем β=h/b=5,5; ξ=0,79; определяем U=86 и V=1,8 и определяем высоту и ширину сечения арки h =882 мм, b = 882/5,5 = 160,4 мм≈160 мм. Принимаем поперечное сечение арки b х h = 160 х 882 мм из 21 слоев толщиной 42 мм. Тогда расчетное сопротивление сжатию и изгибу: Rc = Rи =1*1,2 0,88∙0,95∙1,0∙14/1,0 =140,4 кг/см2 Расчет арки на прочность выполняем в соответствии с указаниями СП 64.13330.2011, п. 6.17, формула (30). Определяем гибкость согласно СП 64.13330.2011, пп. 6.4 и 8.56, формула (9): λ = l0/r = 0,58S/ При определении коэффициента ξ вместо N в формулу (30), п. 6.17, СП 64.13330.2011 надо поставить N7 = -12009,4кг – сжимающее усилие в ключевом сечении для расчетного сочетания нагрузок (рис. 4): ξ = 1 – λ2 N7/(А RcFбр) = 1-762*12009,4 /(3000*140,4*1411,2)=0,883 момент: МД = М/ξ =22003,82/0.883=24919,4 кг*м расчетный момент сопротивления: Wрасч = bh2/6 =20745 см3 Подставив эти значения в формулу (30) СП 64.13330.2011, получим: N/Fрасч+МД/ Wрасч=12009,4/1411,2+24919,4 *100/ 20745 =128,61<140,4кг/см2, т.е прочность сечения обеспечена. Проверим сечение на устойчивость плоской формы деформирования по формуле (38) п. 6.20 СП 64.13330.2011. Покрытие из плит шириной 100 см раскрепляет верхнюю кромку арки по всей длине, откуда lp = 2∙100 cм<140∙b2/(hmб)=140*162/(88,2*0.88)=461,76 см, т.е. имеет место сплошное раскрепление при положительном моменте сжатой кромки, а при отрицательном – растянутой, следовательно, показатель степени n=1 в формуле (38), СП 64.13330.2011. Предварительно определяем: а) коэффициент φм по формуле (25), п. 6.14, СП 64.13330.2011: φм = 140b2Kφ/(hlp) = 140*162*1.13/(88,2*1654)=0.278 Согласно СП 64.13330.2011, п. 6.14, к коэффициенту φм вводим коэффициенты Кжм и Кпм. С учетом подкрепления внешней кромки при m>4 Кжм = 1. Кпм = 0,142lp/h + 1,76 h/ lp+1,4αp=0.142*1654/88,2+1.76*88,2/1654+1.4*0.761=3,82 φм=φм Кпм = 1,06 б) коэффициент φ по СП 64.13330.2011, п. 6.3, формула (8) для гибкости из плоскости: φ = А/λу2 =3000/((0.5*S/(0.29*b)2)=3000/((0.5*3308/(0.29*16)2)=0.0236 Согласно СП 64.13330.2011, п. 6.20, к коэффициенту φ вводим коэффициенты КпN, который при m>4 равен: КпN = 0,75 + 0,06(lp/h)2 + 0,6 αp lp/ h =0,75 + 0,06(1654/88,2)2 + 0,6*0.761*1654/88,2=30,41 φy=КпN =0,73 Подставив найденные значения в формулу (38) СП 64.13330.2011, получим: N/(FбрφRc) + МД/(Wбр φмRи)=12009,4/(1411,2*0.73*140,4)+24919.4*100 /( 20745 *1.06*140,4)=0,89 < 1 Таким образом, условие устойчивости выполнено и раскрепления внутренней кромки в промежутке между пятой и коньковым шарниром не требуется. Расчет опорного узла арки При пролетах арок до 18 м опорные узлы выполняются простым лобовым упором с парными стальными накладками. Требуемая площадь смятия в опорном узле определяется по продольной сжимающей силе. Поперечная сила воспринимается анкерными болтами, заделанными в фундамент, или сварными швами, прикрепляющими стальной башмак к закладной детали фундамента. Стальные накладки башмака крепятся к арке глухарями или болтами. Требуемая площадь сечения анкерных болтов и необходимое количество болтов или глухарей находится по известным формулам. При пролетах более 18 м опорные узлы решаются в виде классических шарниров (рис. 2.38). Опорный башмак арок малых и средних пролетов включает опорный лист с отверстиями для анкерных болтов и две вертикальные фасонки с отверстиями для болтов крепления опорного конца полуарки, которые упираются лобовыми упорами в опорный лист. Зазор между фасонками равен ширине сечения полуарки. Для уменьшения сдвигающих усилий в анкерных болтах опорный башмак устанавливается на наклонную поверхность фундамента, параллельную опорному сечению сегментных арок. Расчет на смятие плиточного шарнира производится по формуле:
где N - продольное усилие в коньковом узле; r - радиус закругления плиточного шарнира (100... 150 мм); l - длина плиточного шарнира (можно принять равной ширине сечения арки b); Rcd - расчетное сопротивление стали диаметральному сжатию при свободном касании, принимаемое по табл. 2 в соответствии с требованиями п. 6.1 СП 16.13330.2011. Расчет крепления стального башмака к арке заключается в проверке условия, чтобы равнодействующая усилий в наиболее нагруженном (крайнем) болте от действия расчетной поперечной силы Q и момента в башмаке Mб не превышала его минимальной несущей способности, по формуле:
где
пш - число срезов; Мб - расчетный момент в башмаке, Мб = Q∙e; e - расстояние от оси шарнира до центра болтового соединения; nб - число болтов в крайнем ряду, параллельном оси элемента; mб - общее количество болтов в башмаке; zi - расстояние между осями болтов в направлении, перпендикулярном оси элемента; zmax - максимальное расстояние между осями болтов в том же направлении. Если это условие не выполняется, то необходимо увеличить диаметр болтов либо их количество и повторить расчет. Затем подбирается требуемый радиус цилиндрического шарнира или требуемая высота плиточного шарнира. В узлах арок вследствие опирания неполным сечением через стальные башмаки (особенно при внецентренном опирании) возникают местные напряжения, которые необходимо учитывать при расчете. Конструктивно эти участки арок усиливаются фанерными накладками на клею, стяжными хомутами или вклеенными арматурными стержнями. Опорные узлы сегментных и стрельчатых арок, в сечениях которых могут действовать изгибающие моменты разного знака и незначительные поперечные силы, центрируются по осям полуарок, и опорный лист располагается перпендикулярно им. Узлы треугольных арок, в сечениях которых действуют в основном положительные изгибающие моменты и значительные поперечные силы, центрируются по расчетным осям, расположенным с эксцентриситетом относительно оси полуарок, а опорный лист башмака располагается перпендикулярно равнодействующей вертикальной и горизонтальной опорных реакций или продольной и поперечной силам в узле. При этом уменьшаются изгибающие моменты в арке и сдвигающие усилия в узле. Концы полуарок для облегчения их шарнирных поворотов в опорных узлах имеют одно- или двусторонние срезки. Опорные узлы большепролетных сегментных арок без затяжек выполняются с применением стальных шарниров качающегося или поворачивающегося типа. Стальные поверхности башмаков отделяются от древесины арок слоем гидроизоляции для предупреждения опасности ее конденсационного увлажнения. Пример расчета узла Рассчитать и запроектировать опорный узел на действие расчетных нагрузок, взятых из таблицы 2.3. Расчетная нормальная сила N = -17274.7 кг (поперечная сила Q = 3749.10 кг (таблица 2.3). Высота сечения 882 мм, ширина 160 мм. Материалы шарнирного соединения в пяте, сталь марки ВСт3кп2 по ГОСТ 380-71* и гнутый профиль из трубы диаметром 50 мм с толщиной стенки 5 мм по ГОСТ 8732-78*.
Решение Проверка напряжений в шарнире на смятие производится по формуле (199), п.15.12.2, СП 16.13330.2011:
Требуемый радиус шарнира:
Конструктивно принимаем стержень d = 40 мм. При этом для гнутого профиля башмака принимаем половину трубы d = 50 мм с толщиной стенки 5 мм. Производим проверку торцевого упора арки на смятие. Расчетное сопротивление смятию Rсм = Rс = Rи = 140,4 кг/см2; Требуемая площадь смятия: Fсм = N/ Rсм = l Исходя их этих размеров, назначаем ширину и длину башмака соответственно 20 и 30 см. Усилие от шарнира передается на башмак через сварной профиль из пластин, имеющий два боковых и одно среднее ребра (рис.2.38). Тогда площадь смятия торца арки под башмаком: Fсм =16∙50 = 800 см2; Напряжение смятия:
Площадь смятия ребер под сварным профилем: Fсм = (2∙4+12)δ = 20δ; Требуемая толщина ребер башмака:
Принимаем ребра толщиной 10 мм. В пределах башмака оголовок работает как плита, защемленная с трех сторон и свободная короткой стороной, с размером в плане 150х140 мм. Максимальный изгибающий момент определяем по формуле: М = αql2 = 0,112∙142∙28,8 =632,2 кг∙см q = N/Fсм = где d - один из размеров участка: α - коэффициент, принимаемый в зависимости от соотношения сторон участка. Для консольного участка d -вылет консоли и α = 0.5. Для участка опертого по четырем сторонам d-меньшая из его сторон, а α - принимается по таблице 2.6. Для участка опертого по трем сторонам, d - длина свободного края, а α - принимается по таблице 2.7. Здесь при отношении менее 0.5 плита рассчитывается как консольная с вылетом, равным длине закрепленного края. Для участка, опертого по двум смежным сторонам d-размер диагонали участка и α - принимается по таблице 2.7. Таблица 2.6 Коэффициент α для расчета плит, опертых на четыре
Коэффициент α для расчета плит, опертых на три стороны, при отношениях длины опертой стороны к длине свободного края (или на две стороны при отношениях длины перпендикуляра, опущенного из угла на диагональ, к длине диагонали). Таблица 2.7
Требуемый момент сопротивления: W = δ2/6 = M/Rу = 632,2 /2300 =0,275 см3, откуда: δ = Принимаем лист толщиной 1,4 см. Концевые части пластины оголовка подвергаются изгибу как консольные от равномерно распределенной нагрузки интенсивностью, соответствующей напряжениям смятия по всей внутренней площадке оголовка от нормальной силы.
Рис. 2.38. Опорный узел арки 1 – стальной шарнир; 2 – боковые ребра опорного башмака; 3 – оголовок; 4 – гнутый профиль; 5 – среднее ребро башмака; 6 – болты; 7 – опорная плита; 8 – накладка; 9 – фундамент q = Nbпл/Fсм = Безопасное расстояние х от края пластины оголовка до ребер башмака определяем из равенства: W = Мконс/(1,2 Rу) =bt2/6 = 20∙1,42/6=431,87 ∙ х2/(1,2∙2∙Rи), откуда: х = Таким образом, конструктивно длину башмака принимаем: а =50-2∙10=30см. На болты, присоединяющие оголовок, действуют усилия, вызываемые поперечной силой при третьей схеме нагружения: Nб = 3749.1 ∙(16+1,4+13,2/3)/50 = 2009,5 кг. Необходимый диаметр болта определим исходя из его несущей способности по изгибу согласно СП 64.13330.2011, п. 7.16: Тб = n∙250∙d2= Nб при n=2; d = Принимаем болты диаметром 24 мм. Расчет конькового узла арки Коньковые узлы арок пролетом до 18 м решаются простым лобовым упором и перекрываются парными деревянными или стальными накладками на болтах. Толщина деревянных накладок принимается равной половине ширины сечения арок. Толщина стальных накладок определяется расчетом (обычно, 10...20 мм). Длина накладок зависит от диаметра, шага расстановки болтов и их количества. Задаются диаметром болтов и расставляют их по длине накладок с учетом требуемых минимальных расстояний между болтами вдоль и поперек волокон древесины. Стальное крепление конькового узла состоит из упорного листа и двух фасонок. Вертикальный упорный лист имеет ширину, равную ширине лобового упора полуарок, и длину, необходимую для постановки двух монтажных болтов, соединяющих полуарки при сборке. Фасонки имеют зазор, равный ширине сечения полуарок, и отверстия для болтов крепления к концу полуарки. В коньковом узле полуарки сегментных и стрельчатых арок соединяются центрированно, а концы треугольных арок - с эксцентриситетами. Для облегчения шарнирных поворотов полуарок в этом узле можно между упорными листами ставить стальную шайбу. Клеедеревянные накладки в коньковых узлах арок имеют толщину порядка 10 см и крепятся к концу каждой полуарки двойными болтами, ближайшими к центру узла, и одиночными болтами у концов накладок. Коньковые узлы арок, работающих в химически агрессивной среде, могут выполняться с помощью вклеенных стальных стержней. При пролетах арок более 18 м коньковые узлы решаются в виде классических (валиковых, плиточных или балансирных) шарниров (рис. 2.39). Конструирование узла начинается с выбора диаметра крепежных болтов и назначения размеров боковых пластин стального башмака из условия размещения болтов. Толщина опорной пластины определяется расчетом (20...40 мм), толщина боковых накладок стального башмака 10...20 мм. Диаметр валикового шарнира определяется из условия его работы на срез и изгиб, обычно 40...80 мм, а щеки башмака проверяются на смятие по формулам СП 16.13330.2011. Высота плиточного шарнира назначается конструктивно (hш=100 мм). Расчет на смятие плиточного шарнира производится по формуле:
где N - продольное усилие в коньковом узле; r - радиус закругления плиточного шарнира (100...150 мм); l - длина плиточного шарнира (можно принять равной ширине сечения арки b); Rcd - расчетное сопротивление стали диаметральному сжатию при свободном касании, принимаемое по табл. 2 в соответствии с требованиями п. 6.1 СП 16.13330.2011. Расчет крепления стального башмака к арке заключается в проверке условия, чтобы равнодействующая усилий в наиболее нагруженном (крайнем) болте от действия расчетной поперечной силы Q и момента в башмаке Mб не превышала его минимальной несущей способности, по формуле
где
пш - число срезов; Мб - расчетный момент в башмаке, Мб = Q∙e; e - расстояние от оси шарнира до центра болтового соединения; nб - число болтов в крайнем ряду, параллельном оси элемента; mб - общее количество болтов в башмаке; zi - расстояние между осями болтов в направлении, перпендикулярном оси элемента; zmax - максимальное расстояние между осями болтов в том же направлении. Если это условие не выполняется, то необходимо увеличить диаметр болтов либо их количество и повторить расчет. Затем подбирается требуемый радиус цилиндрического шарнира или требуемая высота плиточного шарнира. Пример расчета узла Рассчитать и запроектировать коньковый узел на действие расчетных нагрузок, взятых из таблицы 2.3. Расчетная нормальная сила N = -20690.1 кг (РСУ №3), поперечная сила Q = -3508.45кг (таблица 2.3). Высота сечения 882 мм, ширина 160 мм. Материалы шарнирного соединения в коньке, сталь марки ВСт3кп2 по ГОСТ 380-71* и гнутый профиль из трубы диаметром 50 мм с толщиной стенки 5 мм по ГОСТ 8732-78*. Решение Принимаем пластину размером 300х160 мм. Нормальная сила, сжимающая пластину N = 20690.1 кг. Напряжения смятия торца арки в ключе: σсм = N/Fcм = 20690.1 /(30∙16) = 43,1<140,4 кг/см2. Толщину пластины находим из условия ее работы на изгиб по схеме двухконсольной балки, для которой нагрузка: q = 20690.1 /0,3 = 68967 кг/м; Изгибающий момент М = 68967∙0,142/2 =675,88 кг∙м. Требуемый момент сопротивления (с учетом пластичности): W = M/(Rу∙1,2) = 675,88 ∙102/(2300∙1,2) = 24,5 cм3 Требуемая толщина пластины: δ = Принимаем толщину пластины 40 мм. Расчет упорного штыря производим на изгиб как консоли. Изгибающий момент М = Q∙l = 3508.45 ∙4 = 14033,8кг∙см; Требуемый момент сопротивления с учетом пластичности: W = 14033,8/(2300∙1,2) = 5,1 см3; При ширине штыря b = 100 мм требуемая толщина: δ = Принимаем δ = 20 мм. Аналогично рассчитываются спаренные штыри, вваренные справа в опорную пластину. Оголовок и его крепление принимаем таким же, как и в опорных узлах арки. Безопасное расстояние от края пластины оголовка до опорной пластины определяем так же, как при расчете пятового шарнира: х = где: q = 20690.1*16/50/16 = 413,8 кг/см. Тогда длину опорной пластины конструктивно принимаем: 50-2∙10 = 30 см
Стрельчатая арка Пример расчета стрельчатой дощатоклееной арки 3.1.1. Условия примера Запроектировать трехшарнирную стрельчатую арку постоянного сечения, пролет l = 24 м, высота ƒ= 16 м, шаг расстановки арок – B = 4,5 м, фундаменты – железобетонные. Арки проектируются для неотапливаемого склада сыпучих материалов (удобрений). Район строительства – г. Казань. Сосна 2-го сорта; класс ответственности II, γn =1. (рис.3.1). Ограждающая часть покрытия состоит из прогонов с шагом 1.0, 1.5 м, укладываемых непосредственно на арки. По прогонам устраивается кровля из профнастила. Устойчивость арок из плоскости обеспечивается прогонами и деревянными диагональными элементами, которые расположены в торцах здания, образуя поперечные связевые фермы. Прогоны прикреплены к верхним граням арок, а в коньке и в зоне опор полуарок поставлены продольные элементы с упором в боковые грани (распорки).
Рис. 3.1. Конструктивная схема стрельчатой арки
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 991; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.239.79 (0.014 с.) |

 на панели инструментов).
на панели инструментов). на панели инструментов).
на панели инструментов). Рис. 2.37. Диалоговое окно Создание таблицы элементов
Рис. 2.37. Диалоговое окно Создание таблицы элементов
 на панели инструментов).
на панели инструментов). на панели инструментов).
на панели инструментов). V = =
V = =  .
. = 76.
= 76.
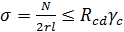


 - равнодействующее усилие в максимально нагруженном болте;
- равнодействующее усилие в максимально нагруженном болте; - минимальная несущая способность одного среза болта;
- минимальная несущая способность одного среза болта; ;
;
 / 140,4 = 123 см2, откуда при b =16cм
/ 140,4 = 123 см2, откуда при b =16cм принимаем l = 40 см.
принимаем l = 40 см.

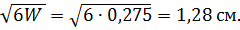



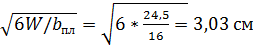

 ,
,





