
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статический расчет стрельчатой аркиСодержание книги
Поиск на нашем сайте
Расчет арки выполняется на сочетания нагрузок: постоянной, снеговой (слева), ветровой (слева), и от загрузочной тележки (рис. 3.3). Опорные реакции от постоянной нагрузки:
Опорные реакции от загруженной тележки:
В связи с тем, что для распорных конструкций более неблагоприятные условия возникают при несимметричном нагружении, рассматриваем схему со снеговой нагрузкой на одном скате. Опорные реакции от снеговой нагрузки на участке левого ската:
где Хс - горизонтальная проекция участка кровли с уклоном до 50°, равная 5,9 м (см. рис. 3.3). Реакции от ветровой нагрузки определяем из условия равенства нулю суммы моментов относительно опорных и ключевого шарниров. - вертикальные:
- горизонтальные:
где Р1, Р2, Р3, Р4 - равнодействующие соответствующих зон ветрового давления; а1,а2,а3,а4 - плечи равнодействующих относительно опорных шарниров; b 1, b 2 - то же относительно ключевого шарнира. Вычислим плечи равнодействующих ветрового давления:
где
Плечи равнодействующих можно также определить графически на ПК. Опорные реакции приведены в таблице 3.3, а изгибающий момент от вертикальных нагрузок - в таблице 3.4. Изгибающий момент: где
Опорные реакции Таблица 3.3
Значения изгибающих моментов от ветровой нагрузки в кН·м приведены в таблице 3.5. Они определены по следующим формулам: - в левой полуарке:
- в правой полуарке:
где моменты от ветровой нагрузки, действующей слева и справа от сечения n:
Значения Mx Таблица 3.4
Примечания: 1. Считаем, что снеговая нагрузка начинается от т. З. 2. Для более точного определения расчетного момента от снеговой нагрузки можно участок между 3 и 4 точками разделить на более короткие отрезки, определить координаты и вычислить изгибающие моменты. Значения изгибающих моментов от ветровой нагрузки, кН·м.
Таблица 3.5
В связи с тем, что в полуарках напряжения от изгиба значительно больше, чем от сжатия, определим расчетные сечения. Для этого сведем в таблицу 3.6 значения M, Q, N от постоянных и кратковременных нагрузок. Основное сочетание нагрузок составляется из постоянных и кратковременных (длительные временные нагрузки в данном проекте отсутствуют).
где Сm- нагрузка от основного сочетания; Pd- постоянные нагрузки; P11- основная по степени влияния кратковременная нагрузка; ψ11=1- коэффициент сочетания, соответствующий нагрузке; ψ12=0,9- коэффициент сочетания, соответствующий нагрузке P12; P13 и т.д.-остальные по степени влияния кратковременные нагрузки; ψ13=0,7 и т.д. соответсвующие коэффициенты сочетания (п.6.4 [3]). По степени влияния в данном примере являются (см.табл.3.6): - по изгибающему моменту: ветровая нагрузка (ψ1=1), снеговая нагрузка на левой полуарке для сечения «3» (ψ2=0,9); - по продольной силе: снеговая несимметричная нагрузка для сечения «1» (ψ1=1); - по перерезывающей силе: ветровая нагрузка (ψ1=1), снеговая нагрузка слева для сечения «1» (ψ1=0,9). Нормальная сила определяется по формуле: N =Qδ·sinφ+HA·cosφ от всех нагрузок, за исключением ветра, т.к. в силу незначительной величины и обратного знака ее можно принять в запас прочности.
Перерезывающая сила Qx определяется по формуле: Qx = Qδ·cosφ-HAsinφ, где Qδ -определяется по балочной схеме. Таблица 3.6
Из сочетания нагрузок видим, что максимальный положительный и отрицательный изгибающие моменты возникают в точке 3 и равен 169,29 кН·м. При других исходных данных номера точек и величина моментов могут не совпадать и значительно разниться. В нашем случае, как отмечалось выше, изгибающие моменты максимальны и близки по модулю.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 591; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.115.187 (0.009 с.) |




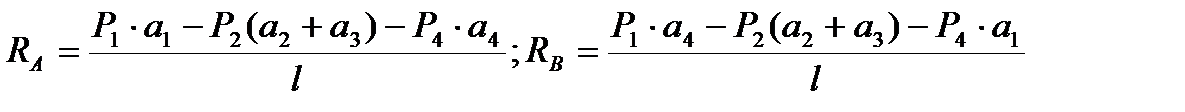







 ;
; 
 ;
; 

 изгибающий момент простой балки от рассматриваемой нагрузки.
изгибающий момент простой балки от рассматриваемой нагрузки.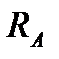




 ,
,













