Т4.1. Что является общим у математических и эвристических методов?

1. Применение математической теории. 2. Учет ограничений по многим ресурсам.

3.Поиск оптимальной очередности заказов. 4. Возможность улучшения качества процесса.

 

Т4.2. Целевая функция в задаче оптимизации процесса предназначена для расчета:

1. Результатов решения задачи. 2. Оценочного показателя качества процесса.

3. Ограничений по ресурсам. 4. Потребности в ресурсе.

Т4.3. Целью применения математических методов в менеджменте не является:

1. Сертификация продукции. 2. Гарантия оптимальности полученного решения.

3. Ускорение процесса решения задачи. 4. Использование готовых программ.

 

Т4.4. Допустимые варианты плана удовлетворяют:

1. Требованиям целевой функции. 2. Требованиям качества продукции.

3. Требованиям ограничений. 4. Потребности в ресурсах.

 

Т4.5. Оптимальный план при ограниченных ресурсах удовлетворяет:

1. Только ограничениям. 2. Только целевой функции.

3. Потребности в ресурсах. 4. Ограничениям и целевой функции.

 

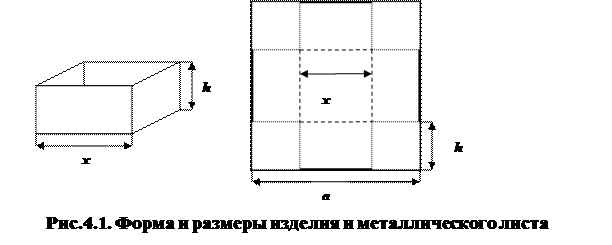
Т4.6. Что не препятствует применению метода линейного программирования?

1. Несоответствие критерия оптимальности реальным интересам предприятия.

2. Нелинейность ограничений и/или целевой функции. 3. Необходимость выбора
очередности выполнения заказов. 4.Наличие ограничений ресурсов.

Глава 4

ОПТИМИЗАЦИЯ ПРОДУКТОВ БИЗНЕС-ПРОЦЕССОВ

ОПИСАНИЕ И АНАЛИЗ БИЗНЕС-ПРОЦЕССОВ

Исходные условия. На предприятии изготавливают для продажи из имеющихся квадратных листов металла с длиной стороны а металлические изделия (рис.4.1) с квадратным основанием, вертикальными стенами и открытым верхом, предназначенные для хранения жидкостей. Технология изготовления изделий следующая: по углам листа делаются одинаковые квадратные вырезы, чтобы получить квадратное основание. Затем оставшиеся части загибаются так, чтобы примыкать своими краями друг к другу, и соединяются с помощью сварки.

Входом в данный процесс являются упомянутые металлические листы, рабочие места для изготовления емкости, оборудование, необходимое для резки, гнутья и сваривания, рабочие соответствующей квалификации, проектная и технологическая документация с указанием размеров вырезаемых кусков и технических условий выполнения производственных операций, необходимые параметры потребляемой энергии и т.д.

ЗАДАНИЕ

 

1. Описать рассмотренный бизнес-процесс. 2. Представить описание процесса с помощью диаграмм системы АРИС.

МЕТОД ВЫПОЛНЕНИЯ

Под бизнес-процессом понимается сеть функций (операций), результат (выход) которых имеет ценность, как для внешнего, так и для внутреннего потребителя. В свою очередь, сеть бизнес-процессов образует бизнес-систему. Например, бизнес-система энергетики состоит из БП производства энергии, БП передачи энергии и БП обеспечения энергией потребителей. Конечный результат на выходе бизнес-системы - электрическая энергия с заданными характеристиками, имеющими ценность для внешнего потребителя (клиента).

Любой бизнес-процесс можно представлять вначале как блок, в котором указаны только его входы и выходы, т.е. без указания функций преобразования его входов в выходы (рис.4.2). Входы и выходы БП устанавливают его границы. Следует вспомнить, что такое описание процесса в системном анализе называлось моделью «черный ящик».

	Рис.4.2. Общее описание бизнес-процесса

 

 

К входам БП относятся материалы, оборудование, люди, энергия, финансы, клиенты, окружающая среда и т.д., используемые в процессе или влияющие на него. Для сравнения, в подобном описании процессов, происходящих в телевизоре, на входе выделяются используемые каналы, положения управляющих органов, электрическая энергия, а на выходе – показываемая программа на экране, яркость, громкость и т.д.

При выделении бизнес-процессов существенное значение имеет его название, так как оно должно определять охватываемые функции. Если процесс назван «Производство продукта», то из этого следует, что в этот процесс не включаются функции проектирования продукта, создания производства и т.д.

БП «Создание изделия» является более широким, так как он охватывает все функции, необходимые для создания продукта. Но он не включает в себя функции сбыта, распределения и продажи продукта. При таком выделении экономическая сторона производства оказывается вне рассмотрения. В результате проектирование может осуществляться только из представлений дизайна продукта, без экономического обоснования.

При совершенствовании БП «Создание и продажа изделия» учитываются затраты на создание продукта и получаемая прибыль от его продажи. Это предполагает максимизацию цены продукта за счет повышения его ценности для потребителя и минимизацию затрат на его создание.
В данном задании требуется описать бизнес-процесс «Создание металлических изделий для хранения жидкостей». Если выходом этого процесса рассматривать созданное изделие, то это будет означать, что процесс охватывает только производство емкости. Описание этого бизнес-процесса в виде «черного ящика» представлено рис.4.3.

Следующим шагом в описании бизнес-процесса является его структурирование, т.е. переход вначале к группам операций, а затем к отдельным операциям в группах. Этот шаг будет рассмотрен ниже на конкретном примере.

Структурирование процесса. В рассматриваемом процессе выделяются следующие группы операций:
1. Подготовка исходного материала для производства работ.
2. Изготовление и отделка емкости.

		Рис.4.2. Представление бизнес-процесса в виде «черного ящика»

 

При детализации группы 1 могут быть выделены такие операции:
Операция 1.1. Поместить лист на рабочий стол.
Операция 1.2. Разметить лист.
Операция 1.3. Отрезать куски по углам

Для группы 2 выделяются:
Операция 2.1. Загнуть оставшиеся части.
Операция 2.2. Сварить соединения.
Операция 2.3. Обработать под покраску и покрасить емкость.

Если для создания емкости размеры изделия и вырезаемых частей листа заданы, то рассматриваемый процесс является достаточно простым. Если же эти размеры надо определить, то требуется дополнительно ввести в процесс группу операций «Проектирование формы изделия».

При проектировании изделия и технологии его производства естественно стремиться к минимизации затрат на его изготовление, обеспечивая при этом требуемое качество. Более широкий взгляд на задачу состоит в учете функции продажи изделия. В этом случае должна рассматриваться ожидаемая прибыль от продажи, зависящая не только от себестоимости выполнения операций, но и от стоимости используемых ресурсов, а также рыночных цен на подобные изделия.

Таким образом, оптимизация БП «Создание и продажа продукта» предполагает взаимосвязанное рассмотрение проектных решений по изделию и технологических аспектов: минимизация используемого материала, в том числе минимизация его отходов при производстве изделий, минимизация энергопотребления при резке и сварке и т.д.

Метод представления описания бизнес-процесса с помощью диаграмм системы АРИС содержится в другой документации.

 

 

ОПТИМИЗАЦИЯ ФОРМЫ ИЗДЕЛИЯ

ЗАДАНИЕ

Определить форму изделия для хранения жидкостей, показанного на рис.4.1, объем которого будет максимальным, в заданных условиях его изготовления из квадратного листа с длиной стороны а = 3,1 + 0,1N м.

МЕТОД ВЫПОЛНЕНИЯ

Для того, чтобы определить форму изделия, надо выяснить, как она влияет на эффективность бизнес-процесса при заданных характеристиках исходного материала. Рассмотрим варианты решения этой задачи для БП «Создание и продажа изделия для хранения жидкости» на числовых примерах.
Вариант 1. Если из квадратного листа с длиной основания а=3 м сделать емкость кубической формы, при которой x = h = 1 м, то для этого надо вырезать по углам квадратные куски шириной 1 м. Объем такого изделия будет равен V = x²*h = 1 м³, а отходы металла S = 4 м².

Вариант 2. Если попытаться для уменьшения отходов металла сделать вырезы шириной 0.1x, т.е. h = 0.1x м, то получим, что V= 0,1x³ м³. Величину переменной x найдем из равенства x + 2 × 0,1x = 3 м. Из него следует, что x = 3/1,2 = 2,5 м, а h = 0,25 м. В результате получим, что

V = 0,1(2,5)³ = 1,56 м³, а отходы составят S = 4×0,25 = 1 м².

Отметим, что в этом варианте формы изделия его объем увеличился более чем в полтора раза, что позволит продавать изделие по большей цене.
Вариант 3. Продолжая уменьшать отходы, примем, что h = 0,05 м. Тогда найдем, что x = 3/1,1=2,73 м, h = 0,135м. При такой форме изделия его объем V = 1,54 м³, а отходы металла S = 0,56 м².

Очевидно, что дальнейшее уменьшение отходов не только не увеличило объем изделия, но даже и уменьшило его.

Если бы критерием эффективности процесса была минимизация потерь металла, то лучшим из рассмотренных вариантов был бы вариант 3. А с точки зрения максимизации объема емкости и, соответственно ему, цены продукта – лучшим является вариант 2. Но при этом нет уверенности, что это самый лучший вариант, так как количество вариантов может быть достаточно большим.

Как найти оптимальный вариант по критерию максимума объема изделия, не перебирая все возможные варианты. Решение подобной задачи возможно только с использованием математических теорий, моделей и методов, гарантирующих оптимальность найденного решения поставленной задачи без перебора всех вариантов.

Формальная постановка задачи оптимизации формы изделия:
Найти длину x квадратного основания изделия, при которой выполняются ограничения:

1) x + 2h = a, 2) x>0, (4.1)

где а – длина стороны квадратного листа,
и удовлетворяется критерий оптимальности V=max.
Целевая функция в данной задаче следующая:

Надо найти max V = x²h. (4.2)

Из ограничения 1 следует, что высота изделия h = (a-x)/2. Подставив это выражение в целевую функцию, получим непрерывную функцию от одного переменного:

V = ax²/2 – x³/2. (4.3)

Для решения задачи в данной постановке следует использовать математический анализ. В нем для непрерывных функций доказан ряд теорем и разработаны методы, позволяющие находить значение переменной, при которой функция имеет экстремальное значение.

Условием экстремума является равенство нулю первой производной от функции. Отсюда следует порядок решения задачи: надо взять первую производную, приравнять полученное выражение нулю и решить уравнение относительно x.

Математический анализ указывает, как взять производную от составной степенной функции. Производная (xⁿ) ′ от степенной функции xⁿ определяется следующим образом:

при n>0 (xⁿ) ′ = n*x^n-1, (4.4)

при n <0 (x ^-n) ′ = -n*x ^-n-1 = -n/x^{n +1}.

Тогда для анализируемой составной степенной функции получим следующее уравнение для первой производной:

V ′ = (аx²/2) ′ – (x^3/2) ′ = ax – 3x²/2 = 0. (4.5)

Так как x не может быть равным нулю (это бы противоречило второму ограничению), то из этого уравнения следует, что x = 2a/3.

В качестве независимой переменной можно было бы выбрать и величину h. Но это усложнило бы решение задачи.

Теперь надо узнать тип экстремального значения. Он может быть либо минимумом, либо максимумом. Для этого надо определить знак значения второй производной в точке экстремума. Функция имеет максимальное значение, если это значение отрицательное. Для запоминания этого способа в математическом анализе было правило, так называемого, «ковшика»: если он стоит так, что из него не выливается вода (его профиль при этом напоминает функцию с минимумом), то это соответствует знаку «+». Если он перевернут, то его профиль похож на функцию с максимумом. При таком положении ковшика вода из него выливается и ему ставится в соответствие знак минус.

Выражение для второй производной будет следующим:
V ″ = a – 3x. (4.6)

При x = 2a/3 получим, что V ″ = -а, т.е. является отрицательным. Следовательно, в найденной точке экстремума функция V = f(x) принимает максимальное значение. Таким образом, решение x = 2a/3 является оптимальным по заданному критерию.

В данном случае вывод о том, что функция V = f(x) имеет максимальное значение для х в интервале [0,3], можно было сделать и простым логическим заключением: на границах интервала V = 0, а в промежутке между ними V > 0.

В точке экстремума объем изделия будет следующим:

V =(2a/3)² × (a-2a/3)2 = (4a²/9) × a/6 = 0,074a³ м³. (4.7)

При а = 3 м получим, что V=1,998 м³, а отходы S = 2 м².

Таким образом, в оптимальном варианте по критерию максимума V изделие будет иметь объем в 2 раза больший, чем в варианте 1 и в 1,25 раза, чем в вариантах 2 и 3.

Системный анализ решения. Итак, была решена задача оптимизации конструкции изделия. Ее результатом стало определение размеров изделия, при которых оно имеет максимально возможный объем. Это позволит соответственно увеличить цену изделия и таким образом увеличит доходы предприятия без дополнительных производственных затрат. Потребуются только затраты на решение задачи, например, на приобретение программного обеспечения.

За счет получился такой результат? За счет лучшего использования материала? Не только, так как самое лучшее использование материала будет при минимальной высоте изделия. Здесь найдена оптимальная форма изделия, т.е. соотношение длины основания к высоте x/ h, равное 4.

Для решения задачи оптимизации формы изделия потребовалось привлечь геометрию и математический анализ. А в реальной ситуации потребовалось бы еще использовать вычислительную математику и информатику для выбора или разработки необходимого информационно-программного обеспечения решения задачи на компьютере.

Сама задача возникла в рамках производственной системы. Ее границами на входе являются имеющиеся материальные ресурсы, трудовые ресурсы, оборудование, производственная инфраструктура, а на выходе – готовое изделие, удовлетворяющее техническим условиям и требованиям к качеству от заказчика.

Если изделие готовится для продажи, то конечным бизнес-процессом в системе будет продажа изделий. Его выходом будет выручка от продажи. В этом случае определение адекватного критерия выбора оптимального решения осуществляется в рамках экономической системы, в которой формируются цены на продукцию, условия продажи и т.д.
Проблемы принятия решений возникают в рамках производственных и экономических систем. А для выработки решений используются создаваемые информационные системы, в которых, в частности, могут реализовываться математические методы. При этом можно выделить следующие этапы решения задачи:

Этап 1. Содержательная постановка задачи.
Этап 2. Математическая постановка задачи.
Этап 3. Выбор метода решения задачи.
Этап 4. Анализ результатов.

В заключение следует отметить, что был оптимизирован продукт бизнес-процесса, а не процесс его изготовления. При оптимизации же процесса производства уменьшаются затраты на его осуществление, например, за счет уменьшения количества передач изделия между рабочими местами и, соответственно этому, ускорения процесса, а также за счет уменьшения общей величины вынужденных простоев из-за несогласованности работ во времени.