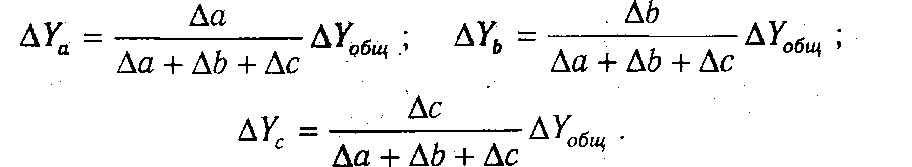Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Способ пропорционального деления и долевого участияСодержание книги
Поиск на нашем сайте
В ряде случаев для определения величины влияния факторов на прирост результативного показателя может быть использован способ пропорционального деления. Это касается тех случаев, когда мы имеем дело с аддитивными моделями типа V =
В первом случае, когда имеем одноуровневую модель типа V= а + b + с. расчет проводится следующим образом:
Методика расчета для смешанных моделей несколько сложнее. Взаимосвязь факторов в комбинированной модели показана на рис. 6.1.
Когда известны Величина коэффициента (К) определяется следующим образом:
Умножив этот коэффициент на абсолютное отклонение В за счет соответствующего фактора, найдем изменение результативного показателя:
В моделях кратно-аддитивного вида сначала необходимо способом цепной подстановки определить, насколько изменился результативный показатель за счет числителя и знаменателя и знаменателя, а затем произвести расчет влияния факторов 2го порядка способом пропорционального деления.
Для решения такого типа задач можно использовать также способ долевого участия. Сначала определяется доля каждого фактора в общей сумме их приростов, которая затем умножается на общий прирост результативного показателя (табл. 6.5):
Графические методы Графические методы связаны с геометрическим изображением функциональной зависимости при помощи линий на плоскости. Графики используются для быстрого нахождения значения функций по соответствующему значению аргумента, для наглядного изображения функциональных зависимостей. Часто графики используются как иллюстрация тех или иных расчетов. В отличие от табличного представления график дает обобщающий рисунок, положение или развитие изучаемого явления, позволяет зрительно увидеть те закономерности, которые содержит числовая информация. В экономическом анализе применяются почти все виды графиков: -диаграммы сравнения, -диаграммы временных рядов, -кривые распределения, -графики корреляционного поля Основные формы графиков, которые используются в АХД, -диаграммы. Диаграммы по своей форме бывают столбиковые, полосовые, круговые, квадратные, линейные, фигурные. По содержанию различают диаграммы сравнения, структурные, динамические, графики связи, графики контроля и т.д. Особенно широко распространены диаграммы сравнения плановых и отчетных показателей. В системе осей координат изображение показывает влияние различных факторов на тот или иной показатель. Графический метод широко применяется для исследования производственных процессов, организационных структур, для анализа эффективности использования производственного оборудования и тд. В математической форм-ой системе анализа, планирования и управления особое место занимают сетевые графики. Они дают большой эффект при моделировании процессов строительства, модернизации. Сетевой график позволяет из всего комплекса работ выделить наиболее значимые и лежащие на критическом пути, сосредоточить на них основные ресурсы организации и координировать их работу. Работы, лежащие на критическом пути, требуют наиболее продолжительного ожидания и наступления очередного события. Основные элементы сетевого графика:-события, - ожидания, - зависимость. При анализе сетевых графиков следует установить, не допущено ли завышение критического пути, учтены ли при оптимизации графика все возможности его сокращения, нельзя ли какие-л. работы выполнить параллельно или сократить время, затраченное на них путем увеличения средств механизации. Это особенно важно в тех случаях, когда продолжительность работ по графику не обеспечивает окончание их в срок. Линейные графики очень широко используются при изучении связей между показателями (графики связи). На оси абсцисс откладываются значения факторного показателя (X), а на оси ординат - значения результативного показателя (У) в соответствующем масштабе. Линейные графики в наглядной и доходчивой форме отражают направление и форму связи. Графики контроля находят широкое применение в АХД при изучении сведений о ходе выполнения плана. В таком случае на графике будут две линии: плановый и фактический уровень показателей за каждый день или другой промежуток времени. Графические способы могут использоваться также при решении методических задач АХД и в первую очередь при построении разнообразных схем для наглядного изображения внутреннего строения изучаемого объекта, последовательности технологических операций, взаимосвязей между результативными и факторными показателями и т.д. Как видим, для построения графиков чаще всего используют первый квадрат системы координат. Здесь важно отметить некоторые требования, которые должны выполняться при построении графиков: 1) выразительность и контрастность рисунка (для этого могут использоваться разноцветные краски); 2) масштаб, который бы обеспечивал наглядность и не усложнял его чтение; 3) не нужно забывать и про эстетичную сторону - график должен быть простым и красивым. Чтобы обеспечить эти требования при построении графика, умышленно прерывают оси координат или берут только отдельные их отрезки, на которых отражается исследуемая информация. Можно также сжимать или растягиватьоси, делать с ними разные преобразования.
|
||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 305; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.195.168 (0.007 с.) |

 Xi и кратно-аддитивного типа
Xi и кратно-аддитивного типа
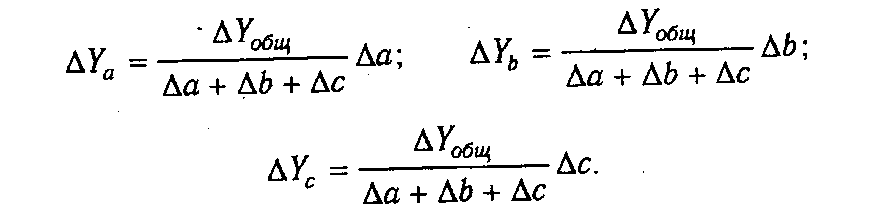

 Вd,
Вd,