
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Смешанное расширение бескоалиционной игры. Равновесие по нэшу В смешанных стратегиях. Свойства и условия существования равновесия по нэшу В смешанных стратегиях.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте игроки выбирают свои стратегии независимо. Тогда для каждой ситуации x(i)=вероятность ее появления будет равна P(x(i))=pi*qj
Доминируемые стратегии игроков в бескоалиционной игре: определение, свойства. Рационализуемые стратегии. Доминирование смешанных стратегий. Определение. Стратегия
для всех В этом случае стратегия Если неравенство (1) выполняется нестрого, но хотя бы для одного набора Свойство. Множество стратегий, выдерживающих такое исключение (оставшихся после удаления) строго доминируемых стратегий, не зависит от последовательности (порядка) исключений. (Для слабо доминируемых стратегий данное свойство может не выполняться.) Замечание. Наличие домин. стратегии у игрока приводит к тому, что он будет пользоваться только этой страт. незав. от выбора других игроков. Тогда его можно искл. из рассмотр. и перейти к редуцированной игре с меньшим числом участников. Если все игроки имеют доминирующие стратегии, то игра имеет решение в доминирующих стратегиях. Решение в доминирующих стратегиях может быть неэффективным (не оптимальным) по Парето. Определение. Стратегия si является лучшим ответом игрока i на набор стратегий оппонентов s-i, если u(si, s-i) ³ u(si ', s-i) при любых si 'ÎSi. Стратегия si является "никогда не лучшим" ответом (НЛО), если не существует s-i, для которых она была бы лучшим ответом. Рациональный игрок не должен играть НЛО, как только он исключает возможность того, что его противники могут играть НЛО и т.д. Стратегии, остающиеся после такого итеративного удаления, — это те стратегии, которые рациональный игрок может оправдать, или рационализовать, разумеется, при некоторых разумных предположениях о выборе своих противников. Определение. Стратегии в Si, которые выдерживают последовательное удаление НЛО называются рационализуемыми стратегиями 10. Задачи игроков в матричной игре (смешанное расширение): аналитическая форма записи. Геометрическая интерпретация решений задач игроков
|
||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 580; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.78.90 (0.007 с.) |

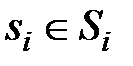 игрока i в игре Г = {I, S, H} строго доминируема (строго доминируется), если существует другая стратегия
игрока i в игре Г = {I, S, H} строго доминируема (строго доминируется), если существует другая стратегия 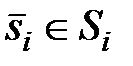 такая, что
такая, что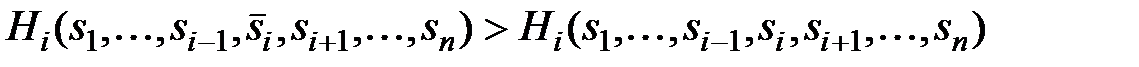 (1)
(1)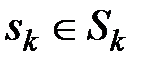 , k = 1, 2, …, i – 1, i + 1, …, n.
, k = 1, 2, …, i – 1, i + 1, …, n.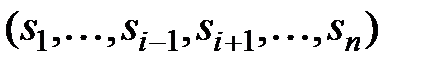 – строго, то стратегия
– строго, то стратегия 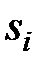 слабо доминируется стратегией
слабо доминируется стратегией 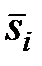 .
.


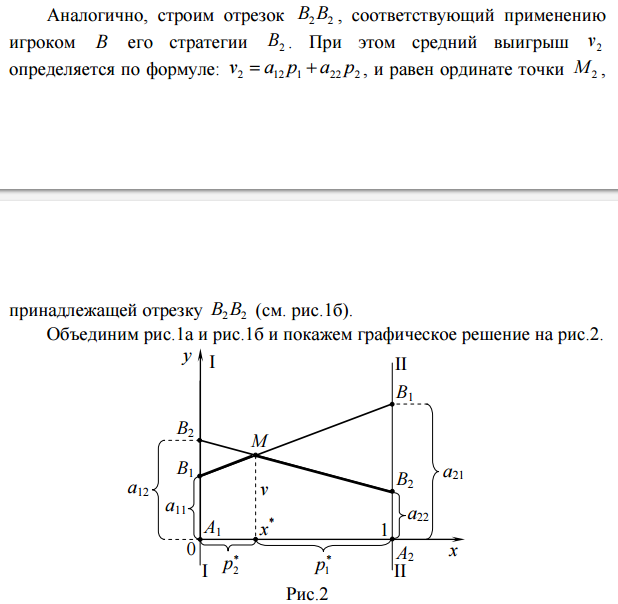 В соответствии с принципом максимина оптимальная стратегия * x такова, что минимальный выигрыш игрока A (при наихудшем поведении игрока B) обращается в максимум. Ординаты точек, лежащих на выделенной ломаной B1MB2, на рис.2 показывают минимальный выигрыш игрока A при использовании им любой смешанной стратегии (участок B1M – против стратегии B1, участок MB2 – против стратегии B2). Оптимальную стратегию определяет точка M, в которой минимальный выигрыш достигает максимума, а ее ордината равна цене игры v.
В соответствии с принципом максимина оптимальная стратегия * x такова, что минимальный выигрыш игрока A (при наихудшем поведении игрока B) обращается в максимум. Ординаты точек, лежащих на выделенной ломаной B1MB2, на рис.2 показывают минимальный выигрыш игрока A при использовании им любой смешанной стратегии (участок B1M – против стратегии B1, участок MB2 – против стратегии B2). Оптимальную стратегию определяет точка M, в которой минимальный выигрыш достигает максимума, а ее ордината равна цене игры v. 


