
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
С-ядро кооперативной игры, его свойства, Принцип оптимальности в форме С-ядра.Содержание книги
Поиск на нашем сайте
Кооперативные игры получаются в тех случаях, когда, в игре n игроков разрешается образовывать определённые коалиции. Обозначим через N множество всех игроков, N ={1, 2,..., n}, а через S – любое его подмножество. Пусть игроки из S договариваются между собой о совместных действиях и, таким образом, образуют одну коалицию. Очевидно, что число таких коалиций, состоящих из r игроков, равно числу сочетаний из nпо r, то есть 1. Принцип оптимальности в форме С-ядра Естественно положить в основу анализа кооперативной игры принцип оптимального распределения максимального выигрыша u(S) между сторонами Реализация этого принципа приводит к рассмотрению С-ядра − множество недоминируемых «вполне устойчивых» дележей кооперативной игры. Вектор x = (x1,..., xn), удовлетворяющий условиям индивидуальной и коллективной рациональности, называется дележём в условиях характеристической функции u. Распределение выигрышей (делёж) игроков должно удовлетворять следующим естественным условиям: если обозначить через xi выигрыш i-го игрока, то, во-первых, должно удовлетворяться условие индивидуальной рациональности xi ³ u(i), для i ÎN, (1) т. е. любой игрок должен получить выигрыш в коалиции не меньше, чем он получил бы, не участвуя в ней (в противном случае он не будет участвовать в коалиции); во-вторых, должно удовлетворяться условие коллективной рациональности т. е. сумма выигрышей игроков должна соответствовать возможностям (если сумма выигрышей всех игроков меньше, чем u(N), то игрокам незачем вступать в коалицию; если же потребовать, чтобы сумма выигрышей была больше, чем u(N), то это значит, что игроки должны делить между собой сумму большую, чем у них есть). Система {N, u}, состоящая из множества игроков, характеристической функции над этим множеством и множеством дележей, удовлетворяющих соотношениям (2) и (3) в условиях характеристической функции, называется классической кооперативной игрой. Делёж x доминирует y, если существует такая коалиция S, для которой делёж xдоминирует y. Это доминирование обозначается так: x > y. Наличие доминирования x > y означает, что в множестве игроков N найдётся коалиция, для которой x предпочтительнее y. Соотношение доминирования возможно не для всякой коалиции. Так невозможно доминирование по коалиции, состоящей из одного игрока или из всех игроков.
Любой дележ из С-ядра устойчив, в том смысле, что ни одна из коалиций не имеет ни желания, ни возможности изменить исход игры. Для того чтобы делёж x принадлежал с-ядру кооперативной игры с характеристической функцией u, необходимо и достаточно, чтобы для любой коалиции S выполнялось неравенство С-ядро может оказаться пустым, например, когда есть слишком сильные коалиции. Если С-ядро пусто, то требования всех коалиций одновременно не могут быть удовлетворены. С-ядро — принцип оптимальности в теории кооперативных игр, представляющий собой множество эффективных распределений выигрыша, устойчивых к отклонениям любой коалиции игроков, то есть множество векторов Свойства Эквивалентным является определение С-ядра кооперативной игры в терминах блокирования распределений выигрыша коалициями. Говорят, что коалиция K блокирует распределение выигрыша x, если найдётся другоераспределение выигрыша y, такое, что Тогда С-ядром кооперативной игры называется множество распределений выигрыша, которые не могут быть заблокированы ни одной коалицией. С-ядро задаётся системой линейных уравнений и нестрогих линейных неравенств, в связи с чем оно является выпуклым многогранником. С-ядро может быть пустым. Достаточные условия непустоты ядра были сформулированы Л.Шепли: Теорема. Кооперативная игра с супермодулярной характеристической функцией имеет непустое ядро.Необходимые и достаточные условия непустоты ядра были сформулированы О.Бондаревой и, позднее,Л.Шепли: Теорема. Ядро кооперативной игры непусто тогда и только тогда, когда она сбалансирована. Любое равновесие Вальраса принадлежит ядру, однако обратное неверно. Однако, при некоторыхпредположенях, если количество агентов в экономике стремится к бесконечности, ядро стремится комножеству равновесий Вальраса (гипотеза Эджворта).
|
|||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 738; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.180.166 (0.011 с.) |

 , а число всевозможных коалиций равно
, а число всевозможных коалиций равно  = 2n – 1.
= 2n – 1. .
. = u(N), (2)
= u(N), (2) .
. , таких, что:
, таких, что:  И для любой коалиции
И для любой коалиции  выполнено:
выполнено:  Где v — характеристическая функция игры.
Где v — характеристическая функция игры. ,И для любого участника
,И для любого участника  выполнено
выполнено 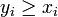 .
.


