Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Какова связь между моментом силы относительно оси и моментом силы относительно любой точки, лежащей на этой оси. Поясните эту связь на рисунке.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
10. Сформулируйте и запишите соответствующие формулы для определения равнодействующей двух параллельных и антипараллельных сил и точки её приложения. 1.Две не равные антипараллельные силы можно заменить равнодействующей, которая равна разности этих сил 2.Две параллельные силы можно заменить равнодействующей, равной сумме заданных сил. Что такое пара сил? Можно ли заменить пару сил равнодействующей? Дайте определение алгеб-раического и векторного момента пары сил.
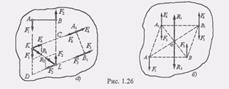
- Численное значение момента пары равно произведению величины одной из сил пары на плечо этой пары. - Сумма моментов сил пары относительно любого центра равна моменту пары. - Момент пары есть вектор, перпендикулярный к плоскости действия пары, направленный в сторону, откуда поворот тела данной парой виден происходящим против хода часовой стрелки. 12. Сформулируйте теоремы об эквивалентности и сложении пар, иллюстрируя эти теоремы соот-ветствующими рисункам и. Т1(1.26.а) Действие пары на абсолютно твёрдое тело не измениться, если пару переместить в другое положение в плоскости ее действия. Т2(1.26.б) действие пары на абсолютно твёрдое тело не измениться, если ее перенести а любую плоскость, параллельную плоскости действия данной пары. Т3(1.27) Действие пары на абсолютно твёрдое тело не измениться, если любым способом видоизменить модули сил и плечо пары, сохраняя постоянным их произведение, т.е. момент пары. Т4(1.28) система пар, действующих на абсолютно твёрдое тело, эквивалентна одной паре, вектор-момент которой равен геометрической сумме моментов слагаемых пар.
Сформулируйте лемму о параллельном переносе силы. Что такое присоединенная пара, чему равен её момент? Всякая сила, приложенная к абсолютно твёрдому телу в данной точке А, эквивалентна той же силе, приложенной в любой другой точке В и паре сил, момент которой равен моменту данной силы относительно новой точки приложения Вектор-момент присоединенной пары сил равен вектору-моменту переносимой силы относительно центра приведения. Дайте определение главного вектора и главного момента произвольной пространственной системы сил и запишите соответствующие формулы. - Сила - Величина
15. Как определить модуль и направление главного вектора и главного момента. Напишите их соответст-вующие аналитические выражения.
16. Сформулируйте основную теорему статики о приведении произвольной системы сил к простейшему виду.
Напишите и сформулируйте векторные и аналитические условия равновесия произвольной про-странственной системы сил. - Запишем условие равновесия в векторной форме:
Для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы главный вектор и главный момент этой системы относительно произвольно выбранного центра приведения равнялись нулю. - Запишем условие равновесия в аналитической форме:
Для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы алгебраические суммы проекций сил на каждую из 3-х осей координат и алгебраические суммы моментов проекций сил на плоскости, перпендикулярные осям относительно точек пересечения этих осей с плоскостями равнялись нулю.
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 417; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.108.144 (0.01 с.) |





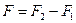
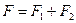
 Система двух равных по величине, антипараллельных и не лежащих на одной прямой сил, называется парой. Пара не имеет равнодействующей, то есть не может быть заменена одной эквивалентной ей силой.
Система двух равных по величине, антипараллельных и не лежащих на одной прямой сил, называется парой. Пара не имеет равнодействующей, то есть не может быть заменена одной эквивалентной ей силой.
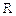 , равная геометрической сумме всех сил данной системы, называется главным вектором.
, равная геометрической сумме всех сил данной системы, называется главным вектором. , равная геометрической сумме моментов всех сил системы относительно центра приведения, называется главным моментом относительно этого центра
, равная геометрической сумме моментов всех сил системы относительно центра приведения, называется главным моментом относительно этого центра ;
; 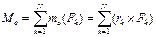
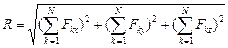 ;
; 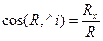 ;
;  ;
; 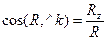
 ;
; ;
; 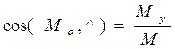 ;
; 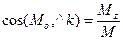

 Произвольная пространственная система сил, действующих на абсолютно твердое тело, в общем случае эквивалентна одной силе, равной главному вектору этой системы и приложенной в произвольно выбранной центре приведения, и главному моменту относительно этого центра приведения.
Произвольная пространственная система сил, действующих на абсолютно твердое тело, в общем случае эквивалентна одной силе, равной главному вектору этой системы и приложенной в произвольно выбранной центре приведения, и главному моменту относительно этого центра приведения. и
и 
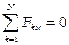 ;
; 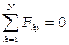 ;
; 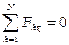
 ;
; 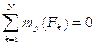 ;
;