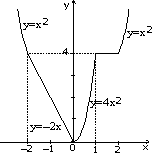Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Как записываются арифметические выражения?Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Арифметические выражения записываются по следующим правилам:
Примеры записи арифметических выражений
Типичные ошибки в записи выражений:
Как записываются логические выражения? В записи логических выражений помимо арифметических операций сложения, вычитания, умножения, деления и возведения в степень используются операции отношения < (меньше), <= (меньше или равно), > (больше), >= (больше или равно), = (равно), <> (не равно), а также логические операции и, или, не. Примеры записи логических выражений, истинных при выполнении указанных условий.
Упражнения
7.1. Запишите по правилам алгоритмического языка выражения:
7.2. Запишите в обычной математической форме арифметические выражения:
7.3. Вычислите значения арифметических выражений при x=1: 7.4. Запишите арифметические выражения, значениями которых являются: б) среднее арифметическое и среднее геометрическое чисел a, b, c, d;
7.5. Вычислите значения логических выражений: 7.6. Запишите логические выражения, истинные только при выполнении указанных условий: 7.7. Начертите на плоскости (x,y) область, в которой и только в которой истинно указанное выражение. Границу, не принадлежащую этой области, изобразите пунктиром.
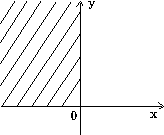
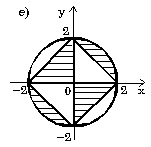
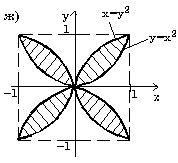
7.8. Запишите логическое выражение, которое принимает значение "истина" тогда и только тогда, когда точка с координатами (x, y) принадлежит заштрихованной области.
7.9. Пусть a =3, b =5, c =7. Какие значения будут иметь эти переменные в результате выполнения последовательности операторов: 7.10. Задайте с помощью операторов присваивания следующие действия: 7.11. Задайте с помощью команд если или выбор вычисления по формулам:
7.12. Постройте графики функций y(x), заданных командами если:
7.13. Определите значение целочисленной переменной S после выполнения операторов:
7.14. Определите значение переменной S после выполнения операторов:
7.15. Составьте алгоритмы решения задач линейной структуры (условия этих задач заимствованы из учебного пособия В.М. Заварыкина, В.Г. Житомирского и М.П. Лапчика "Основы информатики и вычислительной техники", 1989): а) в треугольнике известны три стороны a, b и c; найти (в градусах) углы этого треугольника, используя формулы:
Пояснение. Обратите внимание на то, что стандартные тригонометрические функции arccos и arcsin возвращают вычисленное значение в радианной мере. б) в треугольнике известны две стороны a, b и угол C (в радианах) между ними; найти сторону c, углы A и B (в радианах) и площадь треугольника, используя формулы:
Пояснение. Сначала нужно найти сторону c, а затем остальные требуемые значения;
в) в треугольнике известны три стороны a, b и c; найти радиус описанной окружности и угол A (в градусах), используя формулы:
г) в правильной треугольной пирамиде известны сторона основания a и угол A (в градусах) наклона боковой грани к плоскости основания; найти объем и площадь полной поверхности пирамиды, используя формулы:
д) в усеченном конусе известны радиусы оснований R и r и угол A (в радианах) наклона образующей к поверхности большего основания; найти объем и площадь боковой поверхности конуса, используя формулы:
e) в правильной четырехугольной пирамиде сторона основания равна a, а боковое ребро наклонено к плоскости основания под углом A; найти объем и площадь полной поверхности пирамиды и площадь сечения, проходящего через вершину пирамиды и диагональ основания d; использовать формулы:
7.16. Составьте алгоритм решения задач развлетвляющейся структуры: а) определить, является ли треугольник с заданными сторонами a, b, c равнобедренным; б) определить количество положительных чисел среди заданных чисел a, b и c; в) меньшее из двух заданных неравных чисел увеличить вдвое, а большее оставить без изменения; г) числа a и b — катеты одного прямоугольного треугольника, а c и d — другого; определить, являются ли эти треугольники подобными; д) даны три точки на плоскости; определить, какая из них ближе к началу координат; е) определить, принадлежит ли заданная точка (x, y) плоской фигуре, являющейся кольцом с центром в начале координат, с внутренним радиусом r1 и внешним радиусом r2; ж) упорядочить по возрастанию последовательность трех чисел a, b и c. Ответы — Раздел 7. Алгоритмы. Алгоритмизация. Алгоритмические языки 7.1. а) (x+y)/(x-1/2)-(x-z)/(x*y); б) (1+z)*(x+y/z)/(a-1/(1+x*x)); в) x**(n*(m+2)) + x**(n**m); г) (a+b)**n/(1+a/(a**m-b**(m-n))); д) (a[i]**(2*l) + b[j+1]**(2*k)) * (3**n-x*x*y)/(z-(d[i,j+1]+1)/(z+ y/sqrt(t*t+x*y*z))); е) sqrt(abs(sin(x)**2))/(3.01*x - exp(2*x)); ж) abs(cos(x**3) - sin(y)**2) / (abs(ln(x))**(1/4) + x*y); з) ln(y**(-sqrt(abs(x+1)))) * sin(arctg(z))**2; и) r[i,j]**abs(x-y) - 0.15*abs(sin(exp(-z**8))); к) a**((x+y)/2) - ((x-1)/(abs(y)+1))**(1/3)*exp(-(y+u/2)).7.2. а) 7.3. б) 16; в) 5,5; г) -256; д) 3; е) -2; ж) 1.8. 7.4. б) среднее арифметическое: (a+b+c+d)/4; среднее геометрическое: (a*b*c*d)**(1/4); в) sqrt(x*x+y*y); г) sin(x*3.14/180); д) 6*a*a; е) sqrt(3)*a/2; ж) абсцисса: (c1*b2-c2*b1)/(b1*a2-b2*a1); ордината: (c2*a1-c1*a2)/(b1*a2-b2*a1). 7.5. б) нет; в) да; г) да; д) да; е) нет; 7.6. б) (x < a) или (x > b); в) ((x>=a) и (x<=b)) или ((x>=c) и (x<=d)); г) ((x < a) или (x > b)) и ((x < c) или (x > d)); д) mod(k,2)=1; е) (mod(k,5)=0) и (k > 99) и (k < 1000); ж) (mod(i,2)=1) и (mod(j,2)=0); з) a1*b2=a2*b1; и) (c < a) и (b > a); к) (a=-b) или (a=-c) или (a=-d) или (b=-c) или (b=-d) или (c=-d); л) ((mod(a,2)=0) и (mod(b,2)=0)) или ((mod(a,2)=0) и (mod(c,2)=0)) или ((mod(b,2)=0) и (mod(с,2)=0)); м) (a>0) и (b>0) и (c>0) и (a+b>c) и (a+c>b) и (b+c>a); н) ((a1*b2=a2*b1) и (a1*c2=a2*c1)) или ((a1*c2=a2*b1) и (a1*b2=a2*c1)) или ((a1*c2=b2*b1) и (a1*a2=b2*c1)) или ((a1*a2=b2*b1) и (a1*c2=b2*c1)) или ((a1*a2=c2*b1) и (a1*b2=c2*c1)) или ((a1*b2=c2*b1) и (a1*a2=c2*c1)); о) (y>5-5*x) и (y<5-x) и (y>0); п) (y<5-5*x)) или (y>5-x) или (y<0); р) (a=b) и (c=d) и (b=c).7.7. б)
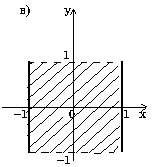
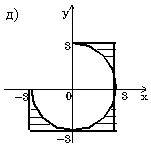
7.8. а) (y>=1-x) и ((y<=0) или (x<=0)); б) (y<1) и (y>=x) и (y>=-x) (вариант ответа: (y<1) и (y>=abs(x))); в) (abs(x)<=1) и (abs(y)<1); г) ((x-1)*(x-1)+y*y<=4) и (y<=3-x) и (y>=x-3); д) (abs(x)<=3) и (abs(y)<=3) и (x*x+y*y>=9) и ((x>=0) или (y<=0)); е) (abs(x)+abs(y)<=2) и (sign(x)<>sign(y)) или (x*x+y*y<=4) и ((y>=2-x) или (y<=-x-2)); ж) ((y>=x*x) или (y<=-x*x)) и ((x>=y*y) или (x<=-y*y)); з) (((x+2)*(x+2)+y*y<=4) и ((x+2)*(x+2)+y*y>=1)) или (x>=-1); и) (((y<=0)=(y>=-x)) или ((x>=0)=(y>=x))) и (x*x+y*y<=1).7.9. б) a=-19; b=-114; c=17; в) a=3; b=1,875; c=15; г) a=7; b=3; c=735; д) a=10; b=2; c=120; е) a=4; b=7; c=3; ж) a=16; b=100, c=11200. 7.10. б) c:=x[1]; x[1]:=x[2]; x[2]:=c; в) a[i]:=(a[i-1]+a[i+1])/2; a[i+1]:=0; a[i-1]:=a[i-1]+0.5; г) u:=max(max(x, y), z) + min(min(x-z,y+z), min(y,z)). 7.11. а) если x <= -100 б) если x*x+y*y <= 1 то y:=sign(x)*abs(x)**(1/7) то z:=x*x+y*y иначе если x < 100 иначе если y>=x то y:=sign(x)*abs(x)**(1/3) то z:=x+y иначе y:=sqrt(x) иначе z:=0.5 все все все все в) если x < 0 г) выбор то z:=lg(-x) при с=0: z:=1 иначе z:=sqrt(x+1) при с=1: z:=x все при с=2: z:=3*x*x - 1/2 если z>=0 при с=3: z:=x*x*x - 3*x/2 то F:=2*z+1 иначе z:=2*x**4 - 3*x/2 иначе F:=sin(z) все все д) если abs(x)+abs(y) < r е) если x>1 то z:=sqrt(x*x+y*y) то если y>1 иначе z:=max(abs(x), abs(y)) то v:=x+y все иначе v:=x-y всеж) если (x-a)**2 +(y-b)**2 < r*r иначе если y>0 то z:=abs(x)+abs(y) то v:=y-x иначе z:=x+y иначе v:=-x-y все все все7.12. б) 7.13. б) 81; в) 21; д) 11; е) 44. 7.14. б) 0; в) 13; д) 52; е) 14. 7.15. б) алг Треугольник1(арг вещ a,b,UgolC, рез вещ c, UgolA, UgolB, S) нач ввод a, b, UgolC c:=sqrt(a*a+b*b-2*a*b*cos(UgolC)) UgolA:=arcsin(a*sin(UgolC)/c) UgolB:=arcsin(b*sin(UgolC)/c) S:=b*c*sin(UgolA)/2 вывод c, UgolA, UgolB, S кон в) алг Треугольник2(арг вещ a,b,c, рез вещ Radius,UgolA) нач вещ p ввод a,b,c p:=(a+b+c)/2 UgolA:=2*arctg(sqrt((p-b)*(p-c)/(p*(p-a))))*180/3.14 Radius:=a*b*c/(4*sqrt(p*(p-a)*(p-b)*(p-c))) вывод Radius, UgolA кон г) алг Объем и Площадь Пирамиды(арг вещ a,UgolAGrad, рез вещ V, S) нач вещ H,SBase,UgolARad | H - высота пирамиды; SBase - площадь основания ввод a,UgolAGrad UgolARad:=UgolAGrad*3.14/180 SBase:=a*a*sqrt(3)/4 H:=a*sqrt(3)/6*tg(UgolARad) V:=SBase*H/3 S:=SBase*(1+1/cos(UgolARad)) вывод V, S кон д) алг Объем и Площадь конуса(арг вещ RBig,RSmall,Ugol, рез вещ V, S) нач вещ H,L ввод RBig,RSmall,Ugol H:=(RBig-RSmall)*tg(Ugol) L:=(RBig-RadSmall)/cos(Ugol) V:=1/3*3.14*H*(RSmall**2 + RBig**2 + RSmall*RBig) S:=3.14*L*(RBig+RSmall) вывод V, S кон е) алг Параметры пирамиды (арг вещ a,UgolA, рез вещ V, S, Sесtion) нач вещ H ввод a,UgolA H:=a*sqrt(2)/2*tg(UgolA) V:=1/3*a*a*H Sесtion:=a*H*sqrt(2)/2 S:=a*a*(1+sqrt(2*tg(UgolA)**2+1)) вывод V, S, Sесtion кон7.16. б) алг Количество положительных(арг вещ a,b,c, рез цел k) надо | k - количество положительных чисел среди чисел a,b,c нач ввод a,b,c; k:=0 если a>0 то k:=k+1 все если b>0 то k:=k+1 все если c>0 то k:=k+1 все вывод k кон в) алг Преобразование(арг рез вещ a,b) надо |меньшее из a,b увеличено вдвое нач ввод a,b если a>b то b:=b*2 иначе a:=a*2 все вывод a,b кон г) алг Подобие треугольников(арг вещ a,b,c,d, рез лог Otvet) дано | a,b и c,d - катеты двух треугольников надо | Otvet=да, если треугольники подобны нач ввод a,b,c,d если (a*d=с*b) или (a*c=d*b) то Otvet:= да иначе Otvet:= нет все вывод Otvet кон д) алг Точки(арг вещ xA,yA,xB,yB,xC,yC, рез лит Otvet) нач вещ DistA,DistB,DistC ввод xA,yA,xB,yB,xC,yC DistA:=sqrt(xA**2 + yA**2) DistB:=sqrt(xB**2 + yB**2) DistC:=sqrt(xC**2 + yC**2) если (DistA < DistB) и (DistA < DistC) то Otvet:="Это точка А" иначе если DistB < DistC то Otvet:="Это точка B" иначе Otvet:="Это точка C" все все вывод Otvet кон е) алг Принадлежность кольцу(арг вещ x,y,r1,r2, рез лог Otvet) дано | r2>r1 надо | Otvet=да, если точка (x,y) принадлежит кольцу | c внутренним радиусом r1 и внешним радиусом r2 нач ввод x,y,r1,r2 если (x*x+y*y<=r2*r2) и (x*x+y*y>=r1*r1) то Otvet:= да иначе Otvet:= нет все вывод Otvet кон ж) алг Упорядочение по возрастанию(арг рез вещ a, b, c) надо | числа a, b, c упорядочены по возрастанию нач вещ t ввод a, b, c если a>b то t:=a; a:=b; b:=t | меняются местами значения a и b все если a>c то t:=a; a:=c; c:=t | меняются местами значения a и c все если b>c то t:=b; b:=c; c:=t | меняются местами значения b и c все вывод a, b, c кон
Глава 8. Технология подготовки и решения задач с помощью компьютера
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 1420; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.169.123 (0.01 с.) |

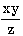

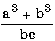
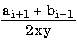
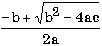
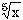 (x<0)
(x<0)
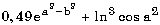
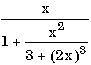
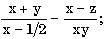
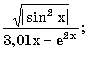
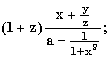
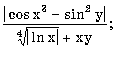
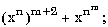
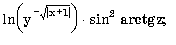
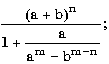
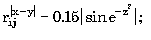
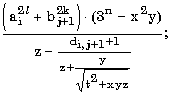
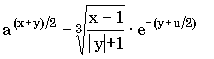
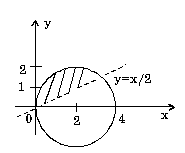
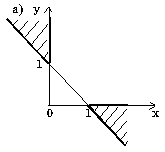
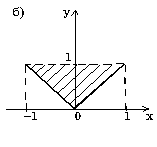

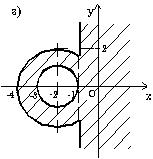
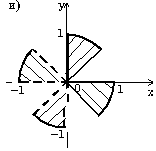
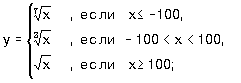
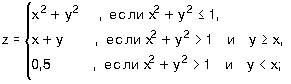
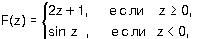 где
где 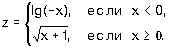
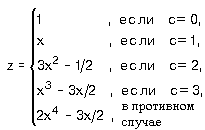
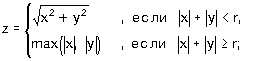
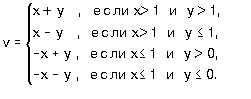
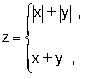
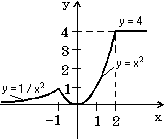
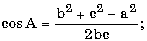
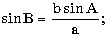
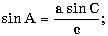
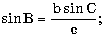
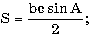 с2 = a2 + b2 - 2ab cos C.
с2 = a2 + b2 - 2ab cos C.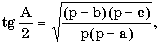 где
где 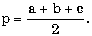
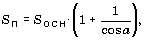

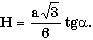
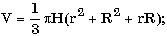

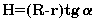
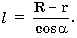
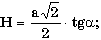
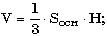
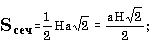
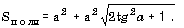
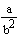 ; б)
; б) 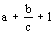 ; в)
; в) 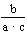 ; г)
; г) 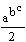 ; д)
; д) 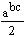 ; е)
; е) 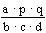 ; ж)
; ж)  ; з)
; з) 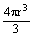 ; и)
; и) 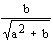 ; к)
; к) 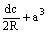 ; л)
; л) 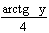 ; м)
; м) 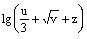 ; н)
; н) 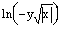 ; о)
; о) 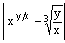 ; п)
; п)  ; р)
; р) 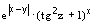 ; с)
; с)  ; т)
; т) 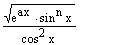 ; у)
; у) 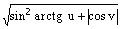 ; ф)
; ф) 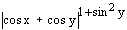 .
.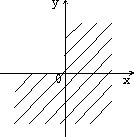 в)
в) 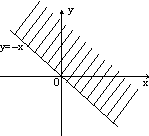 г)
г) 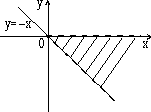 д)
д) 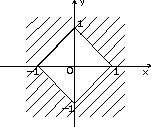 ж)
ж) 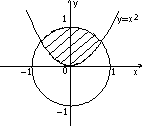 з)
з) 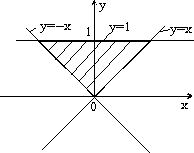 и)
и) 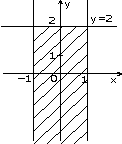 к)
к) 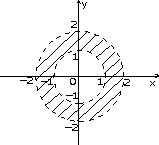
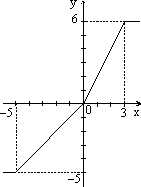 в)
в) 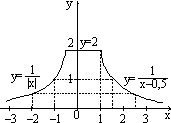 г)
г) 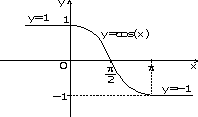 д)
д)